
Matplotlibで音声スペクトルをざっくりとモニタリングする@弱小ボカロP #Granvalley
暑い日が続きますね。こういう時は冷房の効いた部屋で創作活動するのが一番と考えているグランバレイ社員兼弱小ボカロPのGDTY@GVです。
最近、音声を使って何かやってみたい(できれば音声抽出とか)と考えているのですが、知識やスキルが全然足りず苦戦しております。大学時代は音響系の研究をしてたはずなのですが、ほとんどを忘れてしまい一から勉強中です。(そもそも大学時代に理解できていたのか怪しい)
今回ですが、音声処理の勉強がてらに、Pythonでwavファイルを読み込んで、そのスペクトルをMatplotlibを使ってモニタリングできるものを作ってみましたので、それをご紹介いたします。(イコライザーなどで表示されるバー?のようなものをPythonで作ってみようと考えました。)
想定読者
音声解析に興味のある人
Pythonでwavファイルの取り扱い方に興味のある人
Matplotlibのグラフやアニメーションの描画に興味のある人
作ったもの
まず、作ってみたものは以下のようなアニメーションです。以下はQueenのボヘミアンラプソディーの「Mama~」辺りを入力としてみました。音声と合わせてアニメーションさせたいところです。。。(今回はやっていません)
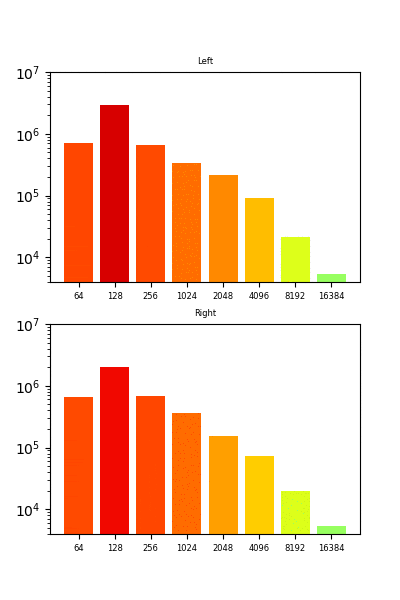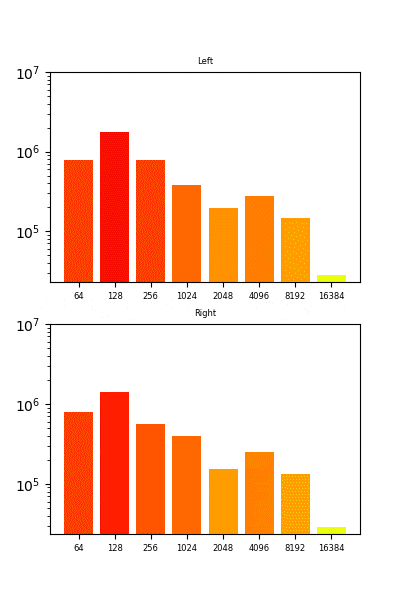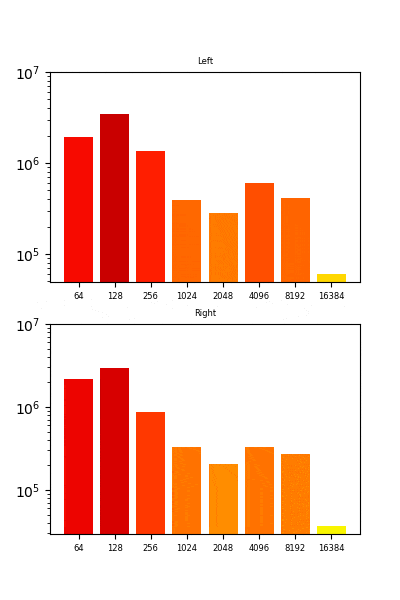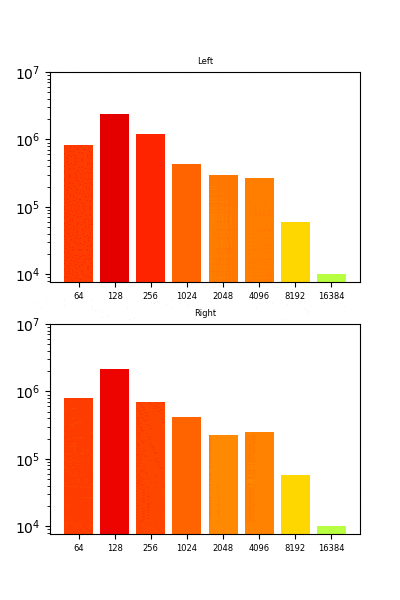
表示している周波数帯は8つです。本来は各周波数帯でフィルタリングする(バンドパスフィルターをかける)のが正かもしれないのですが、今回は各周波数帯で音圧の平均を取っています。
また、音圧が高ければ赤色、低ければ青色となるようにしています。本当は以下のようにしたかったのですが、できませんでした。

実行環境
OS:Windows10
Python:3.7.3
numpy:1.16.2
Matplotlib:3.0.3
コード
コードは以下のような感じです。
まずはライブラリのインポートです。
# wavファイルを扱うためのモジュール
import wave
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
%matplotlib nbagg読み込むwavファイルを指定します。
file = 'hoge.wav'スペクトルを取得する間隔やハミング窓のサイズ(秒数)を指定します。今回は0.25秒を設定しています。
# 何秒間隔でスペクトルを取るか
STEP_TIME = 0.25
# ハミング窓サイズ
WINDOW_TIME = STEP_TIMEスペクトルを取得する関数を定義します。スペクトルの取得はnumpyのrfftを使用します。これは、numpyの高速フーリエ変換を行うための関数の一つです。
# スペクトルを取得する関数
def spectrum(frames, fs):
f = np.fft.rfft(frames)
# 音圧
amp = np.abs(f)
# 周波数
freq = np.fft.rfftfreq(frames.shape[0], d=1.0/fs)
return freq, amp次に、先ほど定義した関数(spectrum)を使い、wavファイルをスペクトルに変換していきます。Pythonでwavファイル扱うために、waveという便利なモジュールがあったので利用してみました。
wave.open()でwavファイルをオープンすると、wavファイルの様々な情報が取得できます。また音声データ自体は、f.readframes(nframes)で取得しますが、このデータはbytes型となっているため、numpyのfrombufferでnumpy配列に変換しています。今回、入力としたwavファイルは量子化ビット数が16のため、dtypeはint16を指定していますが、量子化ビット数が32の場合はint32を指定してください。([1]の箇所)また、今回入力としたwavファイルはステレオとなっているため、左右それぞれのチェンネルにデータを分離させる必要があります。左右のデータはそれぞれ[左, 右, 左, 右...]のように交互に格納されているため、Pythonのスライスを活用して取得しています。([2]の箇所)左右それぞれのデータに分離ができたら、ハミング窓を掛け合わせ、最後に先ほど定義したspectrum関数を使って周波数(..._X)と音圧(..._Y)のスペクトルの情報に変換します。
# 左チャンネルのスペクトルを格納
left_spectrum = []
# 右チャンネルのスペクトルを格納
right_spectrum = []
# wavファイルの読み込み
with wave.open(file, 'rb') as f:
# チャンネル数
nchannels = f.getnchannels()
# 1サンプルのバイト数
sampwidth = f.getsampwidth()
# サンプリング周波数
framerate = f.getframerate()
# フレーム数
nframes = f.getnframes()
# 圧縮タイプ(wavはNone)
comptype = f.getcomptype()
# 圧縮名(wavはNone)
compname = f.getcompname()
# 全フレームを読み込む
frames = f.readframes(nframes)
# Bytesをndarrayに変換(量子化ビット数16を想定)・・・[1]
np_frames = np.frombuffer(frames, dtype= "int16")
# ステップするフレーム数
step_nframes = int(framerate * STEP_TIME * 2)
# ハミング窓のフレーム数
window_nframes = int(framerate * WINDOW_TIME * 2)
# フレームのポジション
pos = 0
# ハミング窓
window = np.hamming(framerate * WINDOW_TIME)
while len(np_frames) > (pos + window_nframes):
# ステレオデータを左右に分離・・・[2]
left_frames = np_frames[pos:pos+window_nframes:2]
right_frames = np_frames[pos+1:pos+window_nframes:2]
# 左右それぞれのフレームにハミング窓をかける
window_left_frames = window * left_frames
window_right_frames = window * right_frames
# 左右それぞれのフレームのスペクトルを取得
left_X, left_Y = spectrum(window_left_frames, framerate)
right_X, right_Y = spectrum(window_right_frames, framerate)
# リストに格納する
left_spectrum.append((left_X, left_Y))
right_spectrum.append((right_X, right_Y))
# 次のポジション
pos += step_nframesX軸(周波数帯)の設定です。
今回は64Hz~16384Hzのうちの8帯域とします。
#プロットする周波数
Freqs = [64, 128, 256, 1024, 2048, 4096, 8192, 16384]
# X軸([0, 1, 2, 3, 4, 5, 6, 7])
X = list(range(len(Freqs)))Y軸(音圧)を取得する関数を定義します。0Hz~64Hzの平均、65Hz~128Hzの平均、129Hz~256Hzの平均、というように各帯域の音圧の平均をとっています。
# Y軸を作成する関数(指定された周波数帯域毎の平均をとる)
def create_Y(spectrum_X, spectrum_Y, Freqs):
Y = []
counter = 0 # Freqs用
tmp = []
for i in range(len(spectrum_X)):
# tmpに音圧を格納
tmp.append(spectrum_Y[i])
if spectrum_X[i] == Freqs[counter]: # Freqsの周波数と一致した場合
avg = sum(tmp) / len(tmp) # 平均をとる
Y.append(avg) # 平均をYに格納する
tmp = [] # tmpを空にする
counter += 1 # カウンタをインクリメント
if counter + 1 > len(Freqs): # カウンタがFreqsの長さを超えたらbreak
break
return Yグラフをアニメーションで描画する部分です。
plotという関数は、アニメーションのフレーム単位で呼ばれる関数です。基本的にplot関数の中でグラフを作ると、それがパラパラ漫画のようにアニメーション化されます。Matplotlibでアニメーションを作るときの注意点ですが、cla関数というグラフをクリアする関数を最初に呼び出さないと、前に描画したグラフの上に新しいグラフが重なって描画されてしまいます。([1]の箇所)
また、今回実装した音圧の大きさによって棒グラフの色が変わるという部分ですが、これはfor文でbar関数を1回1回呼び出して、それ毎に色(color引数)を指定することで実現しています。指定する色はカラーマップから取得しています。([2]の箇所)なお、カラーマップは、plt.get_cmap(カラーマップ名)でMatplotlibに定義されているカラーマップ(cmap)を取得しています。このカラーマップは0.0~1.0の値を入れてやると、その値に応じた色が取り出せるのですが、今回は0.0だと青色、1.0だと赤色になる'jet'というカラーマップを使用しました。([3]の箇所)
最後にちょっとした注意点ですが、縦軸の音圧は対数にすることです。([4]の箇所)私が学生時代に聞いた話では、人間の感覚は対数で感じるとか。周波数の話になりますが、例えばラの音(A3)は440Hzであることが有名ですが、1オクターブ下のラの音(A2)は220Hzで、1オクターブ上のラと音(A4)は880Hzになり、2を底とした対数となります。このように、音圧に関しても、対数で表現したほうがより人間の感覚に近いイメージになります。(間違ってたらすみません。)
fig, (L, R) = plt.subplots(nrows=2, figsize=(8, 12))
# カラーマップ・・・[3]
cmap = plt.get_cmap('jet')
max_Y = 10**7
# グラフプロットするための関数
def plot(i):
index = i % len(left_spectrum)
##### 左チャンネルのグラフ #####
L.cla() # グラフをクリア・・・[1]
L_Y = create_Y(left_spectrum[index][0], left_spectrum[index][1], Freqs)
# 棒グラフを一つ一つ設定する。・・・[2]
for x, y in zip(X, L_Y):
# Y値によって色を変える
L.bar(x, y, color=cmap(math.log(y, 10)/math.log(max_Y, 10)))
L.set_title('Left')
L.set_xlabel('Hz')
L.set_xticks(X)
L.set_xticklabels(Freqs)
L.set_yscale('log', basey=10) # 対数で表示・・・[4]
L.set_ylim(0, max_Y)
##### 右チャンネルのグラフ #####
R.cla() # グラフをクリア・・・[1]
R_Y = create_Y(right_spectrum[index][0], right_spectrum[index][1], Freqs)
# 棒グラフを一つ一つ設定する。・・・[2]
for x, y in zip(X, R_Y):
# Y値によって色を変える
R.bar(x, y, color=cmap(math.log(y, 10)/math.log(max_Y, 10)))
R.set_title('Right')
R.set_xlabel('Hz')
R.set_xticks(X)
R.set_xticklabels(Freqs)
R.set_yscale('log', basey=10) # 対数で表示・・・[4]
R.set_ylim(0, max_Y)
# アニメーションの実行
ani = animation.FuncAnimation(fig, plot, interval=int(STEP_TIME * 1000))
# アニメーションをGIFアニメで保存する場合は以下。(ImageMagickが必要)
# ani.save('hoge.gif', writer="imagemagick")最後のコードをコメントアウトしてますが、これはアニメーションを保存するコードです。GIFアニメで保存する場合はImageMagickを入れる必要があるのでそこだけ注意してください。(MP4でも保存できますが、MP4の場合はffmpegが必要となります)
以上です。
まとめ
まだまだ音声解析については勉強中ですが、今回これを作ってみてwavファイルの扱い方やFFT(高速フーリエ変換)の使い方、Matplotlibでのアニメーションの作り方などが勉強になりました。
最後までご覧頂きありがとうございました!
※グランバレイにご興味のある方はこちらをご覧ください!
この記事が気に入ったらサポートをしてみませんか?
