「〇Xクイズ」と「YesNoクイズ」とでこたえが変わる場合の考察
〇2013年6月28日のツイート
0. はじめに
0-1 文章の目的と動機
来る日も来る日も試験勉強の日々。クイズから離れるストイックな日々が続いて2 カ月が過ぎたある日、試験勉強がひと段落ついたので、気晴らしにTwitter にログインしたよだれねこの目に、非常に興味をそそる一文が飛び込んできた。
【ロブスタ大学教養学部クイズ学科「問題形式学概論」定期試験問題】
「○×クイズ」か「YES・NO クイズ」かで、答えが変わる場合とはどのような場合かについて論じなさい。
( 2013 年6 月15 日 2:40 @jingnakano )
これは!と思い、ちょっとだけぐだめいても罰は当たらないよねぇ…。なんて言い訳しつつ、ほんの10 ツイートほどのつぶやきをするための下書き作成に早速とりかかった。…が、ほんの10 ツイート分の文章を作るつもりが、普段ぐだめけないフラストレーションをぶつけるままにあれよあれよと加筆修正が続き、気が付いたら20,000 字を越える文章に…。
結果的に生じた負の産物がこの駄文でございます。(罰当たって試験に落ちても文句言えないな、うぅ。だけど、まじめな小論文ばかり書いていると、さすがに飽きてくるのろ…。しかたないよね、うん、たまには、まぁ、趣味のクイズに関する論文を書くのもよい気分転換になるかなぁ…なんて。ネタは貯まる一方だし、たまには吐き出さないと。えぇ。チラ裏ですね、はい…。)
ということで、ぐだぐだになりましたが、この文章は「ちょっと気晴らししたいなぁ」という動機で、「上記の問いに答える」ことをとりあえずの目的とする文章です。はい。
駄文中には、問いに回答するための講学上の用語・概念が多分に出てくるので、何言ってだコイツ?状態になるでしょうが、生暖かい目で見てやって下さい。一応、講学上の用語には最低限の解説はつけたつもりですが、詳しい説明や背景までは手間と時間とスペースが許してくれなかったので、触れておりません。えぇ、自己満足ですね。はい…。
なお、この論文は一部に織田信長が相対性理論を発見したレベルの虚偽の事実を交えていますが、これらは実在の人物・団体とは何ら関係ありませんのでご理解ください。また、既にこの世の誰かが提唱した概念を、誤った語法や表現で用いている場合も多分に考えられますが、それに気付いた際は、この概念は○○の世界では××と言うんだよ~とやさしく教えてくれると、めちゃくちゃにうれしがります。お願いしますm(_ _)m
0-2 文章の構成
では、早速、論ずるに当たり論の全体像を示そう。論は主に3 つの部分から構成される。
先ず1章で、問いの解釈について考察する。これは、問題文中の「○×クイズ、YesNoクイズ」、「答えが変わる」が何を指すのかが明確でないことから生じる議論の混乱を避けるためである。次に2章では、その解釈を受けて、考察の対象とするパターンを絞りこみ題意を満たす条件を考察する。続く3章では、2章で導いた条件の具体例が多岐にわたるため、それについて考察を試み、最後の4章で、論をまとめる。という流れになる。
また、本論文の目的から外れるがぐだめき欲を抑えきれなかったので、本論文から派生するトピックをおまけの章として別にもうけた。このおまけの章では、本論の3章で残念ながら具体例を見つけることができなかった部分があったことを受けて、事実制約充足要件の制約を外した「不条理クイズ」の場合を考察し、それを題材にOFPm モデルの観点からのクイズ問題の裏取り・限定確認を見極めるエクササイズを付け加えておいた。
1章 問題文の解釈
提示された問題文には、定義があいまいなため問題文の解釈を困難にしており、問題に答えるために明らかにしておく必要がある事柄が2点ある。
1つ目は『「○×クイズ(あるいはYesNo クイズ)」とはどのようなクイズ形式を指すのか』という点、2つ目は『「答えが違う」とはどのような状態を指すのか』という点である。
この章では、上記2点について順に考察を行い、その結果をうけ、問題文全体としてどのような解釈が妥当かを考察する。
1-1.○×クイズ、Yes-No クイズとはどのようなクイズ形式か?
「○×クイズ」、「Yes・No クイズ」とは、どのようなクイズ形式を指すのだろうか?
この疑問に対して、城島[1990]はクイズ形式アーキテクチャと呼ばれるクイズ形式の表記方法を提唱し、その論文の中で、「○×クイズ」を構成する要件を3つ挙げ、それらの要件を満たす程度により「○×クイズ」を3つのタイプに類型化している。[城島,1990c,12]
この節では、彼女が行った「○×クイズ」の類型を参考に、「○×クイズ」「YesNo クイズ」がどのようなクイズ形式を指すのかを検討する。クイズ形式アーキテクチャの表記方法によると、○×クイズを構成する要件は以下の通りである。
・要件1:「【問題内容】TF 型」
・要件2:「【正誤基準】reply = xi ∈Option 」
補足要件2’:「Option = { x1,…,xn} = { Obj [ 表象:a1],…, Obj [表象:an ] }」
補足要件2’’:「n=2, a1=”○”,a2=”×”」
・要件3:「【正誤基準】if reply = a1 : reply.type = truth
elseif reply = a2 : reply.type = false 」
( 要件0:「【正誤基準】reply = xi ∈frAns 」)
以下、上記の3要件について、詳細な説明を行う。
・1-1-1. 要件1の解釈
要件1はクイズ形式アーキテクチャの表記に従うと、「【問題内容】TF 型」と表わされる。
これは、「出題されるクイズ問題の内容がTF 型である。」という要件である。TF 型クイズ問題とは、A.Lee[1982d]の定義によると、「クイズ問題(Question)の問題文(info)で、あるOFPm ネットワークの組み合わせが示され、それが事実ネットワークと照らし合わせて合致するか否かが問われるクイズ問題の類型」であると定義される。(図1 参照)
図1:TF型クイズ問題

TF 型(True-False type)のクイズ問題の例としては、以下のクイズ問題が挙げられる。
Q1:ニューヨークの.自由の女神像は東京ドームの天井よりも高い。○か×か?
Ans. ×
Q2:現在の日本の首都は東京である?(真か偽か?)
Ans. Obj(意味:True).
また、TF 型クイズ問題はOFP(m)ネットワークの値が問題文中に全て示されているOFPm 完全型クイズ問題であり、「OFP(m)ネットワークの値の一部が抜けており、事実ネットワークと合致するような値が何であるかが問われるクイズ問題の類型」であるOFPm欠落型クイズ問題と区別される。(図2 参照)
Q1,Q2 と対比するようなOFPm 欠落型クイズ問題の例として、以下のようなクイズ問題が挙げられる。
Q3:ニューヨークの自由の女神像と東京ドームの天井で、高さが高いのはどちらでしょう?
Ans. 東京ドームの天井
Q4:現在の日本の首都はどこでしょう?
Ans. 東京
図2:OFPm 完全型問題文とOFPm欠落型


(補足1)Question , info などのクイズ用語の基礎知識
A.Lee は、著書『クイズ用語の基礎知識』シリーズ(1988~)において、クイズに関する考察を行う際に必要となる基礎的な概念の整理を行っている。
彼は、著書の中で、クイズ問題や、問題文、答え、といった言葉のあいまいさを問題として取り上げ、正確に呼び分けるための表現を提案した。彼によると、「クイズ問題(question)」は、「問題文(information)」、「ヒント(clue)」「正解(Answer)」などと呼ばれる部分で構成されるという。(図3 参照)
図3:A.Lee の『クイズ用語の基礎知識』に示されたクイズ問題の構成部分の呼称

(補足2)事実ネットワーク ( 事実行列 )
野間(1987)は、何らかの現象を表現する方法として、Object、Facet、Property という3つの構成要素とそれらのつながり方で表現するOFP ネットワークという方法を提唱した。
そして、このOFP ネットワークを用いて物事の真の姿(イデア)を表現したものを特に事実ネットワークと呼んだ。野間はその後、OFP のみでは表現できない部分を拡張するために、m(その他)という構成要素を追加しOFPm ネットワークとしてモデルの修正・拡張を行った。研究の結果、m にはマロリー拡張やメタパターンといった概念が適用され今日に至っている。
なお、この事実ネットワークを(Obj i ,Facet j ,Property k)とそれらの組み合わせ間のリンクの有無により表現したものを、事実行列と呼ぶ。(図4 参照)
図4:事実ネットワークと事実行列


・1-1-2 要件2の解説
要件2はクイズ形式アーキテクチャの表記に従うと、「【正誤基準】reply = xi ∈Option 」と表わされる。reply というのは回答の内容の事を指し、また、Option とは選択可能な回答の方法の集合を指している。つまりこれは「あらかじめ示された回答の仕方で答えた回答のみを正解とする」という性質をクイズ形式が有することを要件とすることを意味し、言い換えると「あらかじめ指定された方法以外で回答をした場合には誤答扱いとする」と
いう性質を有することを要件とすること意味している。また、要件2には、補足要件として要件2’:「Option = { x1,…,xn } = { Obj [ 表象:a1],…, Obj [表象:an ] }」が付随している。
これは、選択可能な回答方法の集合は要素x1~xn で構成されており、x1~xn にはそれぞれ、表象ファセットのプロパティがa1~an であるObj が対応することを意味している。なお、この要件2と補足要件2’は両者を合わせて、選択肢制約と呼ばれている。そして、特定の「○×クイズ」を指す場合は、この選択肢制約に加え、補足要件2’’「n=2, a1=”○”,a2=”×”」が設定されている。これは、「選択肢可能な回答方法が2つ存在し、その内容として”○”と”×”が設定されている」という性質を持つことを要件とすることを意味している。
・1-1-3 要件3の解説
要件3はクイズ形式アーキテクチャの表記に従うと、「【正誤基準】if reply = a1 :reply.type = truth ↓ elseif reply = a2 : reply.type = false 」と表わされる。この要件は「もし、問題文の内容が真である意思表示を行う場合は「a1(=○)」という意思表示を、もし問題文の内容が偽である意思表示を行う場合は「a2(=×)」という意思表示をしなければ正解としない。」ということを意味している。因みに、要件3はフォース(ある性質が存在しうることの条件)としてクイズ形式が要件1を満たすこと、要件2を満たすことが設定されており、また、要件3は補足要件2’’の拡張要件としての性質を持つ点に注意が必要である。
イメージを具体的にするために、この要件が設定されたクイズ形式では、どのようなことが生じるのか例を挙げよう。例えば以下のクイズ問題を考える。
Q.1: 蚊は虫である。(True or False ? )
frAns. : Obj [意味:True]
上記のようなクイズ問題に対して、要件3が設定されているクイズ形式では、○と答えてTrue の意思表示をする場合には正解として扱われるが、○以外の方法(例えばYes とか、首を縦に振る、など)でTrue の意思表示をした場合、回答内容が一般的な認識の上でTrueの意味を有するものであっても誤答扱いとされるという状況が生じる。
なお、このように、Option に含まれる要素の存在範囲に表象ファセット以外の制約を課すような場合、この制約は羇束的選択肢制約と呼ばれる。[城島,1990b,クイズ問題分類学「選択型クイズ問題に関する考察」]
・1-1-4 要件0に関して
先に括弧つきで示された要件、要件0「【正誤基準】reply = xi ∈frAns 」は、「回答の内容が事実ネットワークの構造と合致しているものを正解として扱う」という要件を意味している。これは「事実と反するような回答を正解と認めることは原則的に認めない」という至極当然と感じられる要件である。この要件は事実制約充足要件と呼ばれるもので、名瀬が「狭義のクイズ問題」を定義する際に用いた構成要件の1つである。この暗黙の了解に対してメスを入れたクイズ問題の類型のひとつとして「不条理クイズ」という事実制約充足要件を満たさない(あるいは、例外規則を設け要件を緩めた)クイズ問題の類型があり、おまけの章でこれを利用していろいろとぐだめくために、ここで言及しておいた次第である。
・1-1-5 「○×クイズ」「YES・NO クイズ」の解釈
以上、3要件について解説をした。これらの要件を満たす程度により、「○×クイズ」というクイズ形式に対して、次の3つの解釈が可能となる。なお、解釈の適用範囲に関する制約の強さは、パターン1がもっともキツくなっている。
○パターン1: 要件①~③を全て満たす。 …「○×クイズ(羇束的)」
○パターン2: 要件①②②’を満たす。 …「正誤判定クイズ」
○パターン3: 要件②②’②’’を満たす。 …「○×回答クイズ」
一般に言われる「○×クイズ」とは、主にパターン2の「正誤判定クイズ」を指している場合が多い、あるいはパターン①と②を区別せず使用しているものと予想される。
なお、「YES・NO クイズ」の解釈に関しては、「○×クイズ」の補足要件2’’の「a1,a2」の値をそれぞれ「Yes,No」に変更したものが、「YesNo クイズ」の解釈になる。
各パターンの具体的な例としては、以下のようなクイズ問題が考えられる。
パターン1:
Q1:人はいつか死ぬ。Ans: ○ (Yes と答えて真偽判定の意思表示をしても誤答)
Q2:人は死なない。 Ans: × ( No と答えて真偽判定の意思表示をしても誤答)
パターン2:
Q3:人はいつか死ぬ。Ans: Obj[意味:True](Yes と答えて真偽の意思表示をしても正解)
Q4:人は死なない。Ans:Obj[意味:False](No と答えて真偽判定の意思表示をしても正解)
パターン3:
Q5:ゼナーカードにある柄は何でしょう? Ans: ○ (波模様、☆、□、+は誤答扱い。)
Q6:アルファベットの大文字でひと筆書きできないのは何? Ans: ×(A,B,E などは誤答)
1-2. 「答えが違う」とはどのような意味か?
問いの文中で表現されている「答えが違う」とは具体的にどのような状況を指すのだろうか?この節では、「答え」とは何か?答えが「どう」違うか?の考察を順に試みる。
・1-2-1 「答え」の解釈
一般に「答え」といった場合、その意味するところは複数存在する1。1 つ目は、「ある正解基準に合致する対象」を意味する「答え」であり、2つ目は「質問に対する応答の内容」を意味する「答え」である。
A.Lee は自身の著書において、これらを区別するために、1つ目の意味での「答え」を「解答」あるいは「AW(アンサーワード)」と呼び、2つ目の意味での「答え」を「回答」あるいは「reply」と呼んで整理をしている。[A.Lee、1988、『クイズ用語の基礎知識63』]
また、彼は翌年出版された著書の中で、AW の中でも特に、「【正誤基準】事実ネットワークに合致している」のみを要件とした時に正答であると判定される要素、あるいはその要素の集合を指して特に、fact-rely AW( frAW )(真の解答)と呼び区別をしている。
[A.Lee,1989,『クイズ用語の基礎知識64』](図5 参照)
以上をまとめると、「答え」とは、以下の3類型に分類される。
①frAW : 正解基準を「事実と合致していること(事実制約充足要件をみたすこと)」のみ設定した場合に、正解とされる要素、あるいはその集合。(真の解答)
(※集合に関しては特にfrAnswer(真の正解)と呼んで区別することもある。)
② AW : クイズ形式に伴う正誤基準制約に照らし合わせ、正解とされる要素、あるいはその集合。(解答)
(※集合に関しては特にAnswer(正解)と呼んで区別することもある。)
③reply : 回答者が出題者側に対して返答する内容。(回答)
図5:frAWとAWとの違い

・1-2-2 答えが「どう」違うかの解釈
「○×クイズ」と「YES・NO クイズ」とでは、それぞれの答えが「どう」違うのだろうか?ここではその解釈として、広い意味と狭い意味との2通りの解釈を取り上げる。
広い意味での解釈としては、『一方のクイズ形式でクイズを実施した際に「答え」として扱われる対象の範囲と、他方のクイズ形式を実施した際に「答え」として扱われる対象の範囲が等しくない。』ことを指して’’違う’’と捉える捉え方が存在する。
一方で、狭い意味での解釈としては、『「○×クイズ」でクイズを実施した際には○が正答で×が誤答扱いだったのに、「YesNo クイズ」でクイズを実施した際にはNo が正答でYesが誤答扱いとなる。(あるいは○と×、Yes とNo とをどちらも逆にした場合)』ことを指して’’違う’’と捉える捉え方が存在する。こちらは○とYes、×とNo という表象が似通った意味を持つ点を考慮に入れた解釈であると言える。
・1-2-3 「答えが違う」の解釈
以上の議論から、「答えが違う」の解釈は、次の6通りが存在すると考えられる。
【狭義の意味で「違う」と解釈した場合】
①「答え」=frAW と解釈した場合:
「○×クイズ」では、frAW に○が含まれ×が含まれなかったのに対して、「YesNo クイズ」では、frAWにNo が含まれYes が含まれない。(または○×、YesNo を逆にした場合)
②「答え」=AW と解釈した場合:
「○×クイズ」では、AW に○が含まれ×が含まれなかったのに対して、「YesNo クイズ」では、AW にNo が含まれYes が含まれない。(または○×、YesNo を逆にした場合)
③「答え」=Reply と解釈した場合:
「○×クイズ」では、回答者が行った回答に○が含まれ×が含まれなかったのに対して、「YesNo クイズ」では、回答者が行った回答にNo が含まれYes が含まれない。(または○×、YesNo を逆にした場合)
【広義の意味で「違う」と解釈した場合】
①’「答え」=frAW と解釈した場合:
「○×クイズ」と「YesNo クイズ」とで、frAW として扱われる要素が異なる。
②’「答え」=AW と解釈した場合:
「○×クイズ」と「YesNo クイズ」とで、AW として扱われる要素が異なる。
③’「答え」=Reply と解釈した場合:
「○×クイズ」と「YesNo クイズ」とで、回答者が行った回答が異なる。
これらの解釈の内、「答え」をReply と解釈する③と③’に関しては、題意を満たし得ることが、深く考察するまでもなく明らかであるので、以後の議論では③の解釈は除外する。
したがって、以後の議論では①②、①’②’を解釈の対象とする。
・1-3 題意の解釈
以上の議論より、「○×クイズ、YesNo クイズ」の解釈については、A:「○×クイズ(羇則的)」B:「正誤判定クイズ」C:「○×回答クイズ」の3類型が、「答え」の解釈としてはx:「frAW」y:「AW」の2類型が、答えが「違う」に関してはⅰ「狭義の解釈」ⅱ「広義の解釈」の2類型が考察に適した解釈として挙げられた。したがって、これらの組み合わせにより、『「○×クイズ」か「YES・NO クイズ」かで、答えが変わる場合とは、どのような
場合か?』という問いに対して、計12 通りの解釈が可能となる。(図6 参照)
図6:問いの解釈のパターン12通りのイメージ


次の章では、この計12 通りの解釈のうち、Axi とCyii の2 パターンを起点として、題意を満たす条件の考察を進めていく。この2パターンを考察の起点に設定した理由としては、先ず、解釈Axi がすべてのパターンの中で最も制約が強い解釈であることが理由として挙げられる。解釈Axi の解釈が最も制約が強いということは、仮に解釈AXi で題意を満たす場合を見つければ、他の11 パターンについても同様に題意を満たすことになる。したがって、その点を考慮すると、Axi を先ず考察の対象とすることは妥当であると言える。また、Cyii の解釈について考察を行う理由は、Cyii の場合に成立する条件をたまたま発見し、考察を進めた結果、題意を満たす場合が数多く存在することが確かめられたためである。したがって、Cyii と制約の範囲が異なる他の解釈に関しても特に題意を満たす条件が存在する可能性があることは注意されたい点である。
以上、1 章の議論をまとめると、題意の解釈として次の2パターンを考察の対象として論を進めることになる。
・解釈①:「○×クイズ(羇束的)」「frAW が狭義の意味で異なる」
「問題文がTF 型であり、True の意思表示をする場合は○、False の意思表示をする場合は×で回答しないと誤答として扱われるクイズ形式と、Trueの意思表示をする場合はYes、False の意思表示をする場合はNo で回答しないと誤答として扱われるクイズ形式とで、問題文で問われている事実に対して正解となるもの(frAW)が異なり、特に、○×クイズではfrAW にTrue が含まれFalse が含まれないが、YesNo クイズではfrAW にTrue が含まれずFalse が含まれる(あるいはそれらの逆)。」場合として、どのような条件を満たす場合が挙げられるのか? について論じなさい。
・解釈②:「○×回答クイズ」「AW が広義の意味で異なる」
「○か×以外で答えたら誤答と扱われるクイズ形式(TF 型で無くても良い)とYESかNO以外で答えたら誤答と扱われるクイズ形式とで、正誤判定基準と照らし合わせ正解として扱われるもの(AW)が異なる」場合として、どのような条件を満たす場合が挙げられるのか?について論じなさい。
2章 題意を満たす条件の考察
1 章では問題文の解釈を行った。その結果、考察を進める起点とする解釈として、①「○×クイズ(羇束的)」で「frAWが異なる」場合と②「○×回答クイズ」で「AW が異なる」場合の2候補に絞り込んだ。この章では、①、②の順に題意を満たす条件を考察していく。
・2-1.解釈①の題意を満たす条件の考察
この節では、『「○×クイズ(羇束的)とYES・NO クイズ(羇束的)」とで「frAW」が「狭義の意味で」異なる』という状態が生じる場合として、どのような条件を満たす場合が存在するかを考察する。そのために、先ず2-1-1 で題意を満たすクイズ問題の例を挙げ、考察の切り口とし、その分析から得られた真理値表を用いて題意を満たすクイズ問題例を探索する。続く2-1-2 では考察をさらに深めるために、名瀬[1988]が提唱した「情報自己更新型問題」というクイズ問題の類型を紹介した上で、2-1-3 で題意を満たす一般的な条件の一つを予想し、その予想に基づき、具体的なクイズ問題の例を数例紹介する。
・2-1-1 真理値表を利用しての題意を満たす具体例の探索
解釈①(Axi)を満たす場合として、どのようなクイズ問題が存在するだろうか?この項では、先ず、解釈Axii を満たすクイズ問題の具体例を一つ挙げ、その問題の分析を元に、簡易的な真理値表を用いて、Axi(解釈①)を満たすクイズ問題を探索する。
先ず、「解釈を満たすクイズ問題って、どんなのがあるかなぁ~?」と適当に思考を巡らせてみた結果、次のクイズ問題が解釈Axii を満たす場合であることが確認できた。
Q1:「あなたの回答は○である。」○か×か?(Yes かNo か?)
Ans. [ ○× ] ○、× [ Yes No ] No
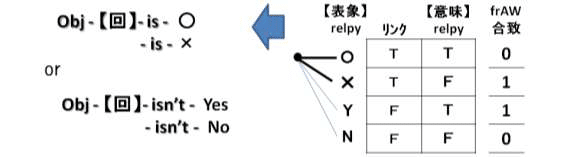
上記のクイズ問題は、「○×クイズ」のクイズ形式では、○と×が正解になり、「YesNoクイズ」のクイズ形式では、No が正解、Yes は不正解となり、「どう違うか?」の広義の解釈を満たしていることが確認できる。このクイズ問題を簡易的な真理値表を用いて分析したものが、以下の図である。(図7 参照)
図7:簡易的な真理値表によるクイズ問題の分析

上の表の見方であるが、左の線は問題文の内容を表わし、「あなたの答えは~である」となる場合の「~」に入るものと左の黒丸とを結んだ線で表わされる。また、リンクの列には、左の線の状況を見て、線が太くなっていたらT,いなかったらFの値が入る。一番右のfrAW 合致の列には、リンクと【意味】reply の値が同じ時(例えば、リンクがT、【意味】リプライがTの時)には1を、異なる場合は0が記入される。
通常、[表象]reply と[意味]reply は固定された値が設定されている。そのため、リンクの列の値か、frAW の合致状況のどちらか一方の値がわかれば、もう一方の値がわかり、真理値表の値がすべて埋まる。
ここで、今知りたいことは、解釈①(Axi)を満たすクイズ問題が何であるかである。解釈①の場合とは、つまるところfrAW の値がfrAW(○,×,Yes,No )=(1,0,0,1)か(0,1,1,0)となる場合である。したがって、真理値表にfrAWの値を入れた以下の2通りの場合を考察し、リンクの値を埋めれば、解釈①を満たすクイズ問題がみつかる。

①frAW (O,X,Y,N) = (1,0,0,1)の場合
【導き方】
1、frAW 合致の列の値を(1,0,0,1)の順に埋める
2、frAW 合致の列の値と【意味】reply の列の値とを比較し、リンクの列の値を埋める
3、リンクの列の値を参照して、Tなら左の線を太くし、Fならそのままにする。
4、完成した図を見て、解釈①に合致するクイズ問題をよみとる。
〇結果
この結果は、以下のクイズ問題に合致する。これは確かに解釈①を満たす。
Q1:「あなたの回答は、○か×である。」○か×か?(Yes かNo か?)
Ans.[OX] ○ [YesNo] No
Q1’:「あなたの回答は、Yes でもNo でもない。」○か×か?(Yes かNo か?)
Ans.[OX] ○ [YesNo] No
②frAW (O,X,Y,N) = (0,1,1,0)の場合
①の場合と同様の手順で結果を導くと、以下のクイズ問題を得ることができる。
Q2:「あなたの回答は、Yes かNo である。」○か×か?(Yes かNo か?)
Ans.[OX] × [YesNo] Yes
Q2’:「あなたの回答は、○でも×でもない。」○か×か?(Yes かNo か?)
Ans.[OX] × [YesNo] Yes
因みに、解釈をAxii に緩めると、以下のクイズ問題も題意を満たすことがわかる。
Q3:「あなたの回答は○である。」○か×か?(Yes かNo か?)
Ans.[OX] ○,× [YesNo] No
Q3’:「あなたの回答は○ではない。」○か×か?(Yes かNo か?)
Ans.[OX] 解なし[YesNo] Yes
Q4:「あなたの回答は×である。」○か×か?(Yes かNo か?)
Ans.[OX] 解なし[YesNo] No
Q4’:「あなたの回答は×ではない。」○か×か?(Yes かNo か?)
Ans.[OX] ○,× [YesNo] Yes
なお、解釈を制約がより緩いB にゆるめ、「○か×かで答える」という制約をはずした場合、Q3’とQ4 は解なしではなく、Q3’はObj[意味:True](ただし、Obj[表象:○]を除く)が正答となり、「ウンウンと、首をたてにうなずく」「Yes と言う」「はいと答える」「ちょっと気取ってOui とフランス語で返答する」などの方法で答えれば、回答が正答として認められうる。なお、この場合は、「○×クイズ」と「YesNo クイズ」で、AW となる範囲がObj[表象:○]とObj[表象:No]の分だけ異なるので、解釈Bxii の場合を満たすことになる。Q4 に関しても、Answer がObj[意味:False]となり、同様のことが生じる。
・2-1-2 Back プロセスと情報更新のタイミングに関する考察
では、上記のクイズ問題に見られる特徴とは何だろうか?そのことを分析するにあたり、名瀬が「クイズ問題の成立要件に関する基礎的考察(名瀬1987f)」の中で提唱した、「情報自己更新型クイズ問題」というクイズ問題の類型について、論文を引用しつつ紹介する。
名瀬は論文中で次のように述べている。
“次に、狭義のクイズ問題の成立要件の3つ目として、「Back プロセスの時点でfrAns.が確定していること」が挙げられる。Back プロセスの終了時点よりも後にfrAns.が確定・収束するクイズ問題、言い換えると、Back プロセスの開始時点以前にfrAns.が未定であるようなクイズ問題は狭義のクイズの要件に合致しない。これらのクイズ問題は「当て物」と呼び区別することを提唱する。例えば…(中略)…事実ネットワークはこのように様々な要因によって変化する。ここで問題となるのが、Back プロセスと事実ネットワークの変動のタイミングが前後する場合である。…(中略)…中でも、Back プロセスから影響を受けて事実が変化しfrAns.が変わってしまうようなクイズ問題も存在する。このクイズ問題を便宜上「情報自己更新型クイズ問題」と名付けておく。’’
「3 章1部クイズ問題の第1 レイヤーの分類に関する諸考察」
名瀬は、事実ネットワークが様々な要因により変化することに言及し、クイズ問題の中でもBack プロセスに伴って事実ネットワークが変化し、frAWが変化するものを指して情報自己更新型問題として類型化した。(図8 参照)
図8:BackプロセスとfrAWの確定状況

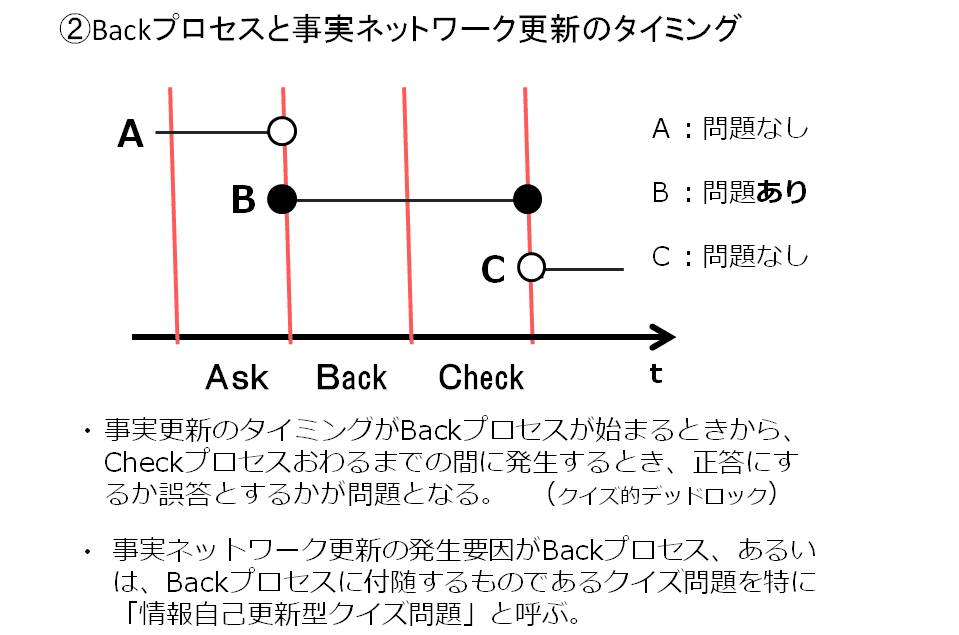
先に2-1-1 で示したQ1~Q4’は、回答するという行為により、事実ネットワークの繋がり方に変化が生じるため、情報自己更新型問題の要件を満たしていると言えよう。ただ、回答の時点においてfrAW が未定であるため狭義のクイズ問題の成立要件を満たさない点には注意が必要である。
※なお、Q1~Q4’は、Back プロセス以前に論理的にfrAWが確定しているため、当て物の中でも極めて高い確実性を伴った当て物に分類される。
・2-1-3 解釈①の題意を満たす条件の考察
2-1-2 では、Back プロセスと事実ネットワーク更新のタイミングに関する考察を紹介した。この分析から、解釈①の題意を満たす条件の1つとして、「Back プロセスが始まる時からCheck プロセスが終わるまでにfrAW に関わる事実が変化」し「変化の結果、○×クイズを実施する際とYesNo クイズを実施する際とでfrAW に含まれるTrue、False の状況が背反的に変化すること」が存在することが予想される。では、このような変化が生じる条件とは、どのようなものだろうか?この項では、2-1-1 で用いた簡易的真理値表を拡張して、題意を満たす条件を探索する。
題意を満たす条件を探索するために、事後事実を拡張した、拡張Ver.真理値表を用いることにする。この表は左から、【表象】reply、題意、事後事実、題意と事後事実の合致状況、【意味】reply、frAWの6列で構成される。通常、【表象】reply,【意味】reply の値は固定されている。通常は、どのような真理値になるかというと、①事後事実を埋める②題意と事後事実を比較して合致状況の値を埋める。③合致状況とreply の意味を比較してfrAWを埋める。という手順を経ると、以下の図9 の右側のようになる。
図9:拡張Ver.簡易的真理値表

これを、解釈①(Axi)の題意を満たすようにする、すなわち、frAW(O,X,Y,N) = (1,0,0,1)or (0,1,1,0)を満たすには、どのような条件のクイズ問題を扱えばよいのだろうか?2-1-1で実施した手順にならい、frAWの値から真理値表の値を逆算し、結果を分析してみよう。
①frAW(O,X,Y,N) = (1,0,0,1)のとき

真理値表は上記のようになる。これを読み解くと、○か×と答えた時の事後事実は題意Aであるのに、Yes かNo と答えると事後事実が¬A(題意A以外)となる場合が解釈①の題意を満たすことがわかった。
②frAW(O,X,Y,N) = (0,1,1,0)のとき

真理値表は上記のようになる。これを読み解くと、○か×と答えた時の事後事実は題意A以外のものとなり、Yes かNo と答えると事後事実が題意Aと同じものとなる場合が解釈①の題意を満たすことがわかった。
したがって、これらの考察より、「一方のクイズ形式で答えた時には、事後事実と題意が合致するような状況が生じるが、もう一方のクイズ形式で答えた時には、事後事実と題意が乖離するような状況が生じる」ことが、解釈①の題意を満たす条件だろうと予想される。
では、この条件を満たすクイズ問題の例には、どのようなものがあるだろうか?適当に例を挙げると以下に示すようなクイズ問題が存在し、いずれも解釈①において題意を満たす場合となっている。
Q1:Yes という回答は多数派である。○か×か?(Yes かNo か?)
(※但し、回答者の人数は2人以上とする。)
Ans.[OX] × [YesNo]Yes かNo(場合による)
Q2:日本の首都は東京である。○か×か?(Yes かNo か?)
(※但し、Yes かNo と回答した時には、この宇宙の因果の理を支配する、人間の力ではどうすることもできないようなスンゲー力が働き、あんなことやこんなことが色々あって、結果、判定者が判定を下す前に、日本の首都が東京でなくなる。)
Ans.[OX] ○ [YesNo] No
Q3:あなたが今食べたパンの枚数は、1枚である。○か×か?(Yes かNo か?)
(※但し、一方のクイズ形式は普通の「YesNo クイズ(羇束的)」だが、もう一方のクイズ形式は、回答の際にパンを1枚食べる必要がある「○×パン喰いクイズ」である。)
Ans.[OX] ○ [YesNo] No
では、順に考察していこう。Q1 は回答者の回答の状況からYes という回答が多数派となるかどうかを問うクイズ問題である。○×クイズの場合は、Yes が多数派になることは絶対にないので、Ans.は×となる。一方で、YesNo クイズでは、回答の結果、Ans.はYes が多数派であればYes に、多数派でなければNo となり、解釈①の題意を満たすものとなる。
しかしながら、Q1 はBack プロセスの前の段階でfrAWの範囲が確定しておらず、また、Back プロセス以前に論理的に答えが確定することもない。したがって、Q1 は狭義のクイズ問題の要件を満たさず、「当てもの」に分類されることになる。それゆえ、解釈①の前提として、狭義のクイズ問題の要件を満たすことが存在していると解釈する場合には、題意に合致しないクイズ問題となる点に注意が必要である。
Q2 は、日本の首都が東京であるかどうかを尋ねる一見普通の問題である……がっ!しかし!あろうことか、○か×と回答した際には何も異変がない一方で、Yes かNo と回答した際には、よくわからない仕組みで首都が東京ではなくなるだ!(ΩΩ<ナ、ナンダッテ!!)という場合を想定している。正式な首都を仙台と定める法律が成立するのか、東京という地名がネオ東京に変化するのか、具体的にどうなるのかはわからないが結果として事実が変わるのである。このような場合も、解釈①の題意を満たしている。しかし、うん、まぁ。あれなので、次に示されたQ3 のような、もう少し現実的なクイズ問題の例を分析しよう。
Q3 は、回答者が回答時に食べたパンの枚数が1枚であるか否かを問うクイズ問題が出題される例である。さらにQ3 では、普通の○×クイズではなく、回答の意思表示をするためには、パンを1枚食べる必要がある○×クイズとなっている。そのため、○×クイズでは、Ans.が○に、一方で、YesNo クイズでは、そもそもパンを食べていないのだからAns がNo となり、これは、解釈①の題意を満たすことになる。ただ、○×クイズとYesNo クイズの制約の強さを比較した時、○×クイズには【回答権獲得】の要件に「パンを1枚食べること」が加わっているため、YesNo クイズより制約が強いクイズ形式であると言える。そのため、Q3 が解釈①の題意に該当するかどうかをより厳密に判断するためには、解釈①の前提として、○×クイズとYesNo クイズとの制約の強さの違いの水準がどこまで設定されているのかを考察する必要が出てくるが、この論文ではその必要性を指摘するに留める。
さて、以上の考察では、回答の表象ファセットのプロパティ値が○,YES の場合には意味ファセットのプロパティ値にTrue が、×,NO の場合にはFalse が設定されていることを前提として考察を進めてきた。しかし、このような捉え方に対して、次のような批判を加えることができる。それは、「英文法のYES・NO は、True やFalse の意味を持つのではなく、返答の内容が肯定文である(YES)か否定文(NO)であるかを本質的には意味することばである。」という批判である。この主張の意味する所としては、英語の否定疑問文に対する回答の方法を考えていただくとわかりやすい。例えば、次の否定疑問文、「Is not capital of Japan Tokyo?」(訳:日本の首都は東京ではない?)に対する問いは、日本の首都は東京であるので、日本語では「違います、東京です」となる。しかし、英語では「No, it is Tokyo」ではなく、「Yes, it is Tokyo」が文法上正しい返答となる。(詳しくは、英語の教科書を参照して下さい。)
したがって、このようにYes・No が返答の内容の肯定・否定を意味する表現であり、命題の真偽を意味する表現ではないとすると、上記の考察で用いた真理値表はYes,No の行の意味の値がT,F と設定されている点で適切ではなくなる。そこで、この点をふまえ、次にYes,No の意味を肯定、否定に変更した真理値表を用いて、解釈①を満たすクイズ問題を探索しよう。
解釈①を満たすクイズ問題を探索するために、図10 の左側に示されるような「簡易的真理値表拡張Ver.2」を用意した。この表は先の拡張簡易真理値表を、Yes の意味を肯定(is)に、No の意味を否定(isn’t)に変更し、Yes、No と回答した際のfrAW の判定方法を、事後事実と回答の意味との合致状況とを比較する方法に変更したものである。図10 の右側は、「日本の首都は東京である」というTF 型クイズ問題を、真理値表に当てはめたものである。
この図を見ると、Yes,No の意味をis,isn’t と変えても、意味をTrue,False と解釈した場合と結果が変わらない事が読み取れる。(このことが、Yes,No の意味を命題の真偽と誤解する原因となっていると思われる。)
図10:簡易的真理値表拡張Ver.2
Q1:日本の首都は東京である

では、解釈①を満たすクイズ問題を探索しよう。題意が肯定の場合と題意が否定の場合のそれぞれに対して、frAW(O,X,Y,N)=(1,0,0,1)と(0,1,1,0)の場合とを考察する。手順とし表を読み取る。の手順で探索を進める。て○×の合致の値を埋める。④○×の合致の値と題意の値を参照して、○×の事後事実の値を埋める。⑤frAW と【意味】reply の値を参照してYes,No の事後事実の値を埋める。⑥表を読み取る。の手順で探索を進める。
( i ) 題意 = is(肯定文) のとき
( a ) frAW(O,X,Y,N) = (1,0,0,1)の場合

( b ) frAW(O,X,Y,N) = (0,1,1,0)の場合

真理値表は上記のようになる。この条件を満たすクイズ問題には次のようなものがある。
Q1: (a) 日本の首都は東京である。○か×か?(Yes かNo か?)
(※但し、Yes,No と答えたときに事実が変わる(首都が東京でなくなる)。)
Ans.[OX] ○ [YesNo] No
Q2: (a) 日本の首都は北京である。○か×か?(Yes かNo か?)
(※但し、○、×と答えたときに事実が変わる(首都が北京になる)。)
Ans.[OX] ○ [YesNo] No
Q3: (b) 日本の首都は北京である。○か×か?(Yes かNo か?)
(※但し、Yes,No と答えたときに事実が変わる(首都が北京になる)。)
Ans.[OX] × [YesNo] Yes
Q4: (b) 日本の首都は東京である。○か×か?(Yes かNo か?)
(※但し、○,×と答えたときに事実が変わる(首都が東京でなくなる)。)
Ans.[OX] × [YesNo] Yes
以上の4つのクイズ問題を総合すると、次のような一般条件が題意を満たす場合として存在することが予想される。それは、「題意=事実であれば、一方のクイズ形式でクイズを実施した際に、題意≠事実となるような変化が生じ、題意≠事実であれば、一方のクイズ形式でクイズを実施した際に、題意=事実となるような変化が生じるようなクイズ問題を扱うこと」である。これは、より一般化すると、「一方のクイズ形式で答えた時には、事後事実と題意が合致するような状況が生じるが、もう一方のクイズ形式で答えた時には、事後事実と題意が乖離するような状況が生じる」という、先に予想した題意を満たす条件と合致する。したがって、題意が肯定である場合はYesNo の意味が真偽であろうが、肯定否定であろうが、解釈①の題意を満たす場合の条件は変わらないことが予想できる。
( ii ) 題意 = isn’t (否定文)のとき
( a ) frAW(O,X,Y,N) = (1,0,0,1)の場合

( b ) frAW(O,X,Y,N) = (0,1,1,0)の場合

真理値表は上記のようになる。この条件を満たすクイズ問題には次のようなものがある。
Q5: (a) 日本の首都は北京ではない。○か×か?(Yes かNo か?)
Ans.[OX] ○ [YesNo] No
Q6: (b) 日本の首都は東京ではない。○か×か?(Yes かNo か?)
Ans.[OX] × [YesNo] Yes
以上の2つのクイズ問題を総合して判断すると、題意が否定文で表現される場合には、次のような一般条件が題意を満たす場合として存在することが予想される。それは、「実施されるすべてのクイズ形式で、事後事実の内容がすべて同一のものになるようなクイズ問題を扱う」ことである。先の題意が肯定文で表現される場合と異なり、back プロセスからcheck プロセス迄の間に事実変化が生じて題意と事実が乖離するような状況が生じた場合は、解釈①の題意を満たさなくなる点に注意が必要である。
・2-2.解釈②の題意を満たす条件の考察
解釈②の条件を満たす場合には、どのような場合があるだろうか?②の制約は①の制約から、「【問題内容】TF 型」の制約をはずし、また、「答え」の解釈を「frAW」から「AW」へと緩くした場合となっている。そのため、2-1 節で考察した条件も、解釈②でも通用する。この節では、特に、解釈①の制約の範囲外で題意を満たす状況が生じる場合について考察を試みる。具体的にはOFPm 欠落型と総称されるクイズ問題について考察する。
・2-2-1 解釈②の題意を満たす具体例の例示
まず解釈②の題意を満たす具体例を1つ挙げて、そこから一般的な条件を抽出してみよう。解釈②の題意を満たす具体例としては、次のようなクイズ問題が挙げられる。
Q1:○か×でお答え下さい。元素記号を1つ挙げなさい。
Ans. : O(酸素)
Q1’:Yes かNo かでお答え下さい。元素記号を1つ挙げなさい。
Ans. : No (ノーベリウム)
上記の例は、○×クイズではAW がO(オー)に、YesNo クイズではAW がNo(エヌオー)になっている。このようなクイズ問題が、解釈②の題意を満たす理由としては、解釈②の場合「○×クイズ」とは要件②を満たすものと解釈されており、③の要件を満たさなくてもよいとしていることが理由として挙げられる。つまり、表象ファセットのプロパティが「○」であることを満たすObj ならば、何でもよいという解釈であるため、上記のクイズ問題は題意を満たすクイズ問題として認められうることになっている。
この例を分析してみると、図11 のようになる。上記のクイズ問題では、info に対するfrAWは一定である。しかし、このうち、事実制約以外の正誤基準制約により、frAWとAW との乖離が生じている(図11)。「○×クイズ」と「YesNo クイズ」では、補足要件②’’が異なるので、前提となる要件②を持つものが「○×クイズ」「YesNo クイズ」であると解釈する限りでは、AW の範囲が異なる。それ故、題意を満たす状況が生じうる。
図11:解釈①の条件と解釈②の条件との対比


・2-3 2章のまとめ
2 章では、1 章での解釈を受けて、解釈①の場合の条件、解釈②の場合の条件を予想した。
その結果、解釈①の場合に題意を満たす十分条件として、「一方のクイズ形式で答えた時には、事後事実と題意が合致するような状況が生じるが、もう一方のクイズ形式で答えた時には、事後事実と題意が乖離するような状況が生じる」場合が当てはまるだろうことが予想された。また、解釈②の場合に題意を満たす十分条件として、「frAW に含まれる○×、YesNo の状況が、frAW (O,X,Y,N) ≠ (0,0,0,0),(1,0,1,0),(0,1,0,1),(1,1,1,1,)」である場合が該当することが予想された。
解釈①の場合には、2-1-2 と2-1-4 で具体的なクイズ問題の例を示したが、解釈②の場合には、条件を満たすクイズ問題の類型が多岐にわたるため、別の章を設けて、具体的なクイズ問題の類型を示すことにする。
3章 解釈②の題意を成り立たせる一条件の具体例
2 章では、解釈②の題意を満たす一条件として「frAWに含まれる○×、YesNo の状況が、frAW (O,X,Y,N) ≠ (0,0,0,0),(1,0,1,0),(0,1,0,1),(1,1,1,1,)」となることがあると予想した。
この章では、この予想を受けて、上記の条件を満たすクイズ問題の類型をOFPm モデルの観点から示す。そのための方針として、AW が複数ある状態の具体例を考察する。
・3-1 OFP モデルとは何か?
まず、OFP モデルについて簡単に説明する。OFP モデルとは、ある対象物(Object)をある切り口(facet)で捉えると、その対象物の特性(property)が表出するという物事の捉え方である。野間[1985]がクイズ問題を分析・分類するために考案した概念である。
その応用範囲は、クイズ問題論、クイズ企画者論をはじめ、クイズ参加者論の強化学の分野にまでわたり、近年では記憶のメカニズムとの関連からの研究が盛んになっている。
OFP モデルは、ABC プロセス、クイズ企画の9 要素、ゲーム決定素と並び、現在の狭義のクイズ論の基礎理論とされており、現在でも様々に拡張・応用がなされている。
図12:OFPモデルのイメージ

・3-2 AW のObj の【表象】ファセットに複数のプロパティ値が存在する場合
Answer に含まれるObject の表象ファセットにプロパティ値が複数存在する場合は、Answer 集合の要素たりうるもの(AW)は複数存在する。例えば、以下の例が該当する。
Q.1:ブッシュ44 代アメリカ大統領が、学部を卒業した大学は何でしょう?
Ans. イェール大学(エール大学、Yale University)
例をみると、要するに、解答となるもの1つに対して様々な表現方法がある場合にAWが複数存在するであろうことが予想される。「ブッシュ44 代アメリカ大統領が、学部を卒業した大学は何でしょう?」という問いに対して、Answer の要素たり得るもの(AW)としては「アメリカにあるアイビーリーグの1つであるYale university」で限定されるObject(真実のイェール大学)が存在するが、このObject の表象ファセットに着目した場合、プロパティ値として、「イェール大学」「エール大学」「イェールユニバーシティ」など少なくともAnswer たりうるプロパティ値が3つは存在するため、AW が複数になっている。
以上の考察を踏まえた上で、解釈②の題意を満たす場合の条件としては、「AW に含まれるObject の【表象】ファセットに複数のプロパティ値が存在する結果AW が複数となり」かつ「正誤判定基準の変化に伴い、一方のクイズ形式では○(or×)がAW に含まれ、他方のクイズ形式ではNo(orYes)がAW に含まれるようなクイズ問題を扱う(すなわち、frAW≠(0,0,0,0),(1,0,1,0),(0,1,0,1),(1,1,1,1) )」という条件があることが予想される。この条件を満たす例としては、以下に示すクイズ問題が挙げられ、これは解釈Cyii を満たしていることが確認できる。
Q2:Yes かNo でお答え下さい。日本式の天気記号で快晴を表わす記号は何でしょう?
Ans.解なし
Q2’: ○か×でお答え下さい。日本式の天気記号で快晴を表わす記号は何でしょう?
Ans.○
次に、より制約がきつい解釈である解釈Cyi の例を考察する。解釈Cyi の例を見つけるためには、表象ファセットに「○」と「No」、あるいは、「×」と「Yes」が設定されているObject がAW となるようにすればよい・・・のだが、これはどうもなかなか見つからない。
そこで、指示表象と呼ばれる概念を援用して具体例を探すことにする。指示表象とは、表象Facet の中でも特に、一定の合意の下で、例外的に妥当性を認められたProperty 値に対するFacet のことを指す。(図13 参照)
指示表象を用いたクイズ問題で題意②の解釈を満たすようなものとしては、例えば、次のようなものが該当する。
Q3:オセロで使う駒は、2種類である。
(選択肢): ○:「No」 ×:「Yes」 △:「どちらでもない」 □:「わからない」
Ans.○「No」
四択クイズの選択肢を示す表現(ABCD や1234 など)が○×△□に置き換わった状態をイメージして頂きたい。上記のクイズ問題では、No と答えたい時の代替的な表現として「○」という表現で意思表示を出題側に伝えることが認められている。そのため、false の意思表示をするために、No と答えても、指示表象である○と答えても正答として扱われる。(ただ、○とNo それぞれが持つ意味ファセットのプロパティ値が互いに対立する性質を持つも
のであるため、デザイン的にはあまり好ましくない。…と一言付け加えておく。)
このようなクイズ問題が成立することを考慮すると、「○の指示表象にNo が、×の指示表象にYes が設定されている場合」または「No の指示表象に○が、Yes の指示表象に×が設定されている場合」で、「正誤判定基準の変化に伴い、一方のクイズ形式では○(or×)がAW に含まれ、他方のクイズ形式ではNo(orYes)がAW に含まれるようなクイズ問題を扱う」場合が、解釈Cyi の例を満たす場合に該当することが予想できる。
図13:指示表象のイメージと、その具体例

・3-3 info 中のfacet の対プロパティ限定力が弱い場合
info(問題文)中のファセットが複数通りの解釈ができる場合も、AW が複数となり得る。
例えば、以下のクイズ問題が該当する。
Q1:ブッシュ44 代アメリカ大統領の、出身大学はどこでしょう?
Ans.イェール大学、ハーバード大学
上記の例の問題文を、簡易の情報形で表現すると、以下の通りになる。
[ O,F,P ] P = [ブッシュ(m:44 代アメリカ大統領), 出身大学 , 0 ]
上記の例ではファセットの表象である【出身大学】が、大学だけでなく大学院なども含みうる表現であるため、上記の問題文は「ブッシュ~が学部を在籍した大学はどこでしょう?」や「ブッシュ~が在籍した大学院はどこでしょう?」という複数の解釈が可能となり、結果としてAW が複数存在する状態が発生じている。
以上の考察をふまえた上で、解釈Cyii の題意を満たす場合の条件としては、「info 中のfacet の対プロパティ限定力が弱いため、複数のfrAW が存在し」かつ「frAW(O,X,Y,N)=(0,0,0,0),(1,0,1,0),(0,1,0,1),(1,1,1,1)でない」という条件が存在することが予想される。この条件を満たすクイズ問題は、以下のようなものが挙げられる。
Q2: Yes かNo でお答え下さい。日本語の「はい」を意味する外国語は何でしょう?
Ans. Yes
Q2’: ○か×でお答え下さい。日本語の「はい」を意味する外国語は何でしょう?
Ans.解なし
上記のクイズ問題は、まぁ…うん。一応解釈Cyii の題意を満たす場合ではあるけれど、3-2で示した問題例と区別がわかりづらい上、○×クイズのAnswer が解なしとなっているので、より適当な例を探したい所である。そのため、次にグループファセットと呼ばれる概念を援用して具体例を探すことにする。
グループファセットとは、info 中のObj の下位クラスに含まれる複数のObj をプロパティ値として持つファセットのことを指す。グループファセットを持つクイズ問題で題意を満たす例としては、以下のクイズ問題が該当する。
Q3:○か×でお答え下さい。元素記号を1つ挙げなさい。
Ans. : O(酸素)
Q3’:Yes かNo かでお答え下さい。元素記号を1つ挙げなさい。
Ans. : No (ノーベリウム)
図14:グループファセットとは?

・3-4 info 中のObj の表象ファセットのプロパティ値が持つ、対Obj 限定力が弱い場合
info(問題文)中のObj の表象ファセットのプロパティ値が持つ、対Obj 限定力が弱い場合も、AW が複数となり得る、例えば、以下のクイズ問題が該当する。
Q1:ブッシュ大統領が、取得した学士号は何でしょう?
Ans.経済学士、歴史学士
上記の例の問題文を簡易の情報形で表現すると、以下のようになる。
[ O,F,P ] P = [ブッシュ大統領, 所持:学士号 , 0 ]
上記の例では、Object の表象である「ブッシュ大統領」が、第44 代アメリカ大統領のブッシュのみならず、彼の父である第42 代アメリカ大統領のブッシュも含みうる表現となっている。そのため、上記の問題文は、「パパブッシュが取得した学士号~」や「子ブッシュが取得した学士号~」という複数の解釈が可能になり、結果としてAW が複数存在する状態が生じている。
以上の考察を踏まえた上で、解釈②を満たすクイズ問題を考えよう…考えよう…考えても、制約がきつすぎて、現実的なうまい例を見つけることができなかった。残念。そのため、この節では、理論上、解釈②を満たす状況が発生しうることを指摘するに留める。
以上、3-2 節~3-4 節より、解釈②を満たしうる場合は以下の図のようになる。これらは、単独でのみ成り立つのではなく、複数の場合が同時に成り立つ場合もあることに注意が必要である。
図15:OFP の限定力に起因して、AW が複数となる場合

・3-5 その他(クイズ問題の構造がmultiple の要件を満たす場合)
上記の例以外にAW が複数存在する例も存在する。寺窪が『クイズ問題構造論概論』[1992]の中で示したクイズ問題の1類型である、マルチプルと呼ばれるパターンが該当する。
マルチプルとは、一回の出題(Ask)に対してクイズ問題が2つ以上出題される構造をもったクイズ問題であり、Answer の範囲には各info のAW が含まれ、その内のどれか一つ以上を回答すれば正答として扱われる(図16 参照)。
具体的な例としては、複数のクイズ問題が提示され、その内のどれかを選んで回答するクイズや、一度に2つの問題が同時に読み上げられる多重音声クイズなどがこの類型に該当する。このマルチプルで各クイズ問題のAW がすべて同じものでなければAW が複数存在することになる。(例えば、Q1.蚊は死ぬ?とQ2.人間は死ぬ?をマルチプルで出題しても、どちらもAW はObj[意味:True]でありAW は複数とならない。)
したがって解釈②の題意を満たす条件としては、「クイズ問題がマルチプルの要件を満たす上で、各AW が複数となり、正誤判定基準の変化に伴い、一方のクイズ形式では○(or×)がAW に含まれ、他方のクイズ形式ではNo(orYes)がAW に含まれるようなクイズ問題を扱う」ことが存在するだろうことが予想される。
因みに、題意を満たす現実的な例では、次のようなクイズ問題が挙げられる。
【多重音声クイズ】同時に読まれる問題文を聞いて、解答を回答して下さい。
Q1:粉チーズやスモークチーズなどチーズにも色々ありますが、地中海に浮かぶ島国、マルタ島で生まれたことから名前がつけられた、愛玩用の小型犬といえば何チーズでしょう?
Q2:沖縄県那覇市にある饅頭屋「ぎぼまんじゅう」が製造・販売している、赤い食紅で大きく描かれたひらがなの「の」の字が特徴的な饅頭は、何まんじゅうでしょう?
Ans.Q1:マル(チーズ) Q2:のー(まんじゅう)
【わかったもの勝ちクイズ】:次のクイズ問題のどれかの解答を回答すれば正答とします。
Q3:『死刑台のエレベーター』や『地下鉄のザジ』などの映画を制作したことで知られる、フランス人映画監督は誰でしょう?
Q4:ハルツームまで続く白ナイル川の起点となっている、南スーダンにある湖は何湖でしょう?
Ans.Q3 (ルイ・)マル: Q4:ノー(湖)
図16:種々のクイズ問題構造

4章 まとめ
以上、解釈を2パターンに分け、題意を満たす場合の条件とその具体例について考察を行った。当初に示された問いへの回答としては、以上の議論から次のようになる。
『「○×クイズ(羇束的)のクイズ形式でクイズを実施する時とYES・NO クイズ(羇束的)のクイズ形式でクイズを実施する時とで、frAW が変化し、一方のクイズ形式ではfrAWが○(または×)に、他方のクイズ形式ではfrAW がNo に(またはYes)なる場合」が生じるための十分条件としてはどのようなものが存在するか?』と題意を解釈した場合の回答としては、「一方のクイズ形式で答えた時には、事後事実と題意が合致するような状況が生じるが、もう一方のクイズ形式で答えた時には、事後事実と題意が乖離するような状況が生じるようなクイズ問題を扱うこと」が上記の解釈を満たす場合を成立させる十分条件の1つである。という回答をすることができる。
また、『「○×回答クイズのクイズ形式でクイズを実施する時とYES・NO 回答クイズのクイズ形式でクイズを実施する時とで、AW が変化し、一方のクイズ形式がAW とする対象の範囲と他方のクイズ形式がAW とする範囲が異なる場合」が生じるための十分条件としてはどのようなものが存在するか?』と題意を解釈した場合の回答としては、「frAW の状況が、(O,X,Y,N) ≠ (0,0,0,0),(1,0,1,0),(0,1,0,1),(1,1,1,1)であるクイズ問題を扱うこと」が上記の解釈を満たす場合を成立させる十分条件の1つである。という回答ができる。
○参考論文
A.Lee(1982)、「True or False – type Question」
野間(1985)、「OFP モデルと事実ネットワーク」
名瀬(1987)、「クイズ問題の成立要件に関する基礎的考察」
城島(1990)、「選択型クイズ問題に関する考察」
城島(1990)、「統一的なクイズ形式記述方法に関する考察~クイズ形式アーキテクチャ~」
○参考書籍
A.Lee(1988)、『クイズ用語の基礎知識 63』、民明書房
A.Lee(1989)、『クイズ用語の基礎知識 64』、民明書房
寺窪(1992)、『クイズ問題構造論概論』内守堂
よだれねこ(1998)、『よだれのぐだめき~企画篇~』、情報中央出版
澤木恭介(2000)、『クイズ論2000』日本クイズ学会
5章 おまけ
このような冗長でチラ裏ちっくな文章に目を通して頂きありがとうございます。この分析は、問題解決を目指した、クイズの可能性を追求した、クイズをより楽しむための手段としての研究である狭義のクイズ論体系の研究から得られた様々な知見から、基礎的な部分を引用して行われました。はて?クイズ論とは何ぞや?という方もいらっしゃいましょう。クイズ論とは、明確な定義はないですが、クイズに対する話題・考察・意見・感想・研究etc など、クイズに関するもの全般を指す言論のこと、くらいの意味をもった言葉でしょう。これは先に挙げた狭義のクイズ論と対比され広義のクイズ論と呼ばれ区別されます。広義のクイズ論と狭義のクイズ論とが区別され、学問として研究が進み始めたのは1980年代の頃で、アメリカ人のA.Lee らを中心にQuizology として誕生した経緯があります。誕生してから25,6 年程とまだ学問としては歴史が浅いですが、1980年代末には日本にも輸入され、各研究者により精力的な研究が行われました。その研究の結果、現在までに、クイ
ズを楽しむ人々に貢献する数々の知見が研究成果として得られています。この文章を読んだことをきっかけに、目的志向・問題解決志向のクイズ論(狭義のクイズ論)の世界の拡がりと可能性を感じ取って頂けたのなら嬉しい限りでございます。
…とまぁ、作り話はここまでにして、さて。では、おまけの本題に入りましょう。この章では、3-4 で具体的なクイズ問題の例を見つけられなかったことから、不条理クイズと呼ばれるクイズ形式を採用した場合に、どのようなクイズ問題が成り立つのかを、思考実験として行う…予定だったんですが、この章を書いている間に試験まで1週間を切ったので、予定を変更して、読んでいただいている方々へ、恐れ多くも逆に試験問題を提示したいと思います。はい。具体的には、以下のような問いになります。
問.事実制約充足要件を課さないクイズ形式(『不条理クイズ』)を実施する場合、以下のクイズ問題が嘘問とされる、あるいは限定があまいとされるパターンとしては、どのような場合が考えられるかを論じなさい。
Q1:北区や南区が設置されている、日本の首都である都市はどこでしょう?Ans.東京
「嘘問」というのはinfo のAWに対する限定力が0であるクイズ問題を指します。また、「限定が甘い問題」というのはinfo のAW となるObj に対する限定力が1(well-pinned)とならないクイズ問題を指します。
上記の問いを考察することで、クイズ問題の作問時の1プロセスである「裏取り・限定確認」に役立つ着眼点が発見できる…気がします。余力がある方は、お時間があるときに考察してみて下さい。
ここまで、読んでいただきありがとうございました。…あ、あと最後に言い忘れていたことが一つ。
「swk~the final~公式記録集」
クイズ関連委託販売のQuiket 様にて、販売中です!
( http://quiket.biz/products/detail.php?product_id=71 )
※現在は、販売しておりません。
→2023年8月にリバイバルしました😆
https://swkstamina.booth.pm/
(終)
いいなと思ったら応援しよう!

