02 The Elements of Game Theory ①The core concepts ②Maximally Exploitative Strategy ③Counter Exploitation
The Core Concepts
以下は、本書を通じてゲーム理論を論じる際に使用される重要な概念である。
ゲーム理論
知的で合理的な意思決定者間の対立や協力の数学的モデルを研究する数学と科学の全分野。経済学、軍事戦術、政治、心理学、生物学、コンピュータサイエンス、ポーカーなどのカードゲームに適用できる。
ゲーム
プレーヤーと呼ばれる複数の人々の間の相互作用で、各プレーヤーのペイオフが他のプレーヤーによってなされた決定の影響を受けるもの。
効用 Utility
プレイヤーが特定の結果から得る幸福の総合的な尺度。
効用の数値が高いほど、その結果が好ましいことを意味する。
ゼロサムゲーム(Zero-Sum Game)
ある参加者の効用における利益または損失が、他の参加者の損失または利益と正確に釣り合う状況を数学的に表現したものである。
参加者の利益の合計と損失の合計を差し引くと、合計がゼロになる。(ポーカーは、レーキやトーナメントのファイナルテーブルやSNGで使われるICM [Independent Chip Model]を無視すれば、ゼロサムゲームである。これについては、この本の後半で勉強することになる)。
戦略(Strategy)
プレイヤーの行動に関する完全な仕様であり、ゲーム中のあらゆる可能な決定点においてプレイヤーが取るであろう各行動を記述したものである。
純粋戦略(Pure Strategy)
同じ決定ポイントで常に同じアクションを取る戦略。
混合戦略(Mixed Strategy)
純粋戦略(Pure Strategy)と呼ばれるもので、同じ決定点において、ある確率で2つ以上の純粋戦略をとる戦略。
支配的戦略(Dominant Strategy)
他のプレイヤーがどの戦略を選んでも、ある戦略が他の戦略より高いペイオフを得ること。他のプレイヤーのアクションに関係なく、その戦略が他の戦略より小さいペイオフを獲得する場合、その戦略は支配的である。
異なる2つの戦略A、Bについて。
♦Bは厳密にAを支配する
Bを選ぶと,他のプレイヤーが何をしても,Aを選ぶよりも常に良い結果になる場合.
♦BがAを弱く支配する
BがAより優れている相手の行動のセットが少なくとも1つあり、他のすべての相手の行動のセットがBにAと同じペイオフを与えている場合。
♦B は A に厳密に支配されている
Bを選ぶと、他のプレイヤーが何をしようと、常にAを選ぶよりも悪い結果になる場合。
♦B は A に弱く支配されている
BがAより悪い結果をもたらす相手の行動が少なくとも1セットあり、他のすべての相手のアクションがAにBと同じペイオフを与える場合。
♦BとAは自動詞である(?)
相手のアクションによって、Aを選んだ方が良い場合もあれば、Bを選んだ方が良い場合もある。
Maximally Exploitative Strategy(MES) 最大エクスプロイト戦略
最大エクスプロイト戦略とは、相手の固定戦略に対して最も収益性の高い反応(アクションのセット)である。MESを計算するためには、相手の全戦略を知らなければならない。MESを求めるには、特定のハンドを一つ一つプレイしていく中で、最も儲かる方法を見つければよい。それがわかれば、ゲーム全体の価値は個々のハンドのEVの総和となる。
ホールデムの1,326種類のハンドの組み合わせの中で、最も収益性の高いプレイが分かれば、MESを見つけたことになる。各ハンドは常に最も収益性の高い方法でプレイされるので、あるハンドが2つ以上の異なる方法でプレイされる場合(混合戦略)、それぞれのアクションのEVは同じでなければなりません。次のような単純化されたポーカーの状況を考えてみましょう。
ゲーム例:
Game: Heads-Up Sit N’ Go (Players can only push or fold)
BNスタック:100チップ
BBスタック :100チップ
ブラインド (5/10)
プリフロップ: BNは自分のハンドを全部使ってオールインする作戦をとっています。BBのMESはBNに対してどうでしょうか?
ポットオッズの公式を使うと

BBはVillainのレンジに対して45%以上のエクイティがあるハンドは全てコールできるので、BBの対BNのMESは66.21%のハンドをコールして33.79%をフォールドします(ハンドレンジ18)。
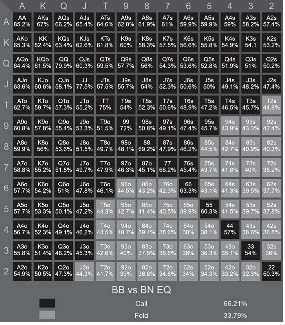
ハンドレンジ18:
最低でも45%のエクイティを持つコールレンジ
各ハンドのEV計算は独立して行われるため、単独で+EVのハンドはすべてコールされ、-EVのハンドはすべてフォールドされます。全体の戦略や「バランス」、あるいは自分のレンジを守るために、あるハンドを本来より少なくプレイする「ロスリーダー」タイプのプレイというものは存在しないのです。それぞれのハンドは利益を生むか生まないかのどちらかであり、それに従ってプレイされるべきなのです。
BBのMES(すべての+EVハンドをコールし、すべての-EVハンドをフォールドする)の各ハンドの組み合わせ頻度に加重した集計EVは、15チップのポットから13.77チップ、これはポットの92%です(ハンドレンジ19)。

ハンドレンジ19:
BBのMESを計算する
BNのエクスプロイト戦略(100%のハンドでオールインする)の集計EVは:15チップのポットから1.2228チップ、これはポットの8%です(ハンドレンジ20)。

ハンドレンジ20:
BNの搾取的戦略の集計EV
Counter Exploitation カウンターエクスプロイト
MESは相手の固定戦略に対して計算されますが、適応的な相手は自分の戦略を新しい戦略に修正することができ、その戦略は順番に自分のMESに対して最大限の搾取を行い、相手の期待値を向上させることができるのです。
例
先ほどの例で、BNが10bbですべてのハンドをオールインするシンプルな戦略をとった場合を考えてみましょう。BBのMESは66.21%のハンドをコールし、残りの33.79%のハンドをフォールドすることであった。BNはBBのコール戦略を知っていれば、BBを最大限に利用するためにプッシュ戦略を調整することができる。
私たちのEV方程式を各ハンドに適用することで、どのBNハンドが+EVショブになるかを見つけることができます。
![]()
すべてのハンドのEVをハンドで計算するのは非常に時間がかかるので、HRC(Hold'em Resources Calculator)(holdemresources.net)のような押し順アプリを使うこともできる。
2回目の反復
BNのカウンターエクスプロイトは、46.61%のハンドをシャブし、53.39%のハンドをフォールドすることです(ハンドレンジ21)。

ハンドレンジ21:
BNカウンターエクスプロイト
次に、BBも戦略を変えて、新しいBN戦略に対する最適な対応を見つけることができる。
3回目の反復
BBのベストレスポンスは、30.3%のハンドをコールし、69.7%のハンドをフォールドすることです(ハンドレンジ22)。

ハンドレンジ22:
BBベストレスポンス
このような両者の反調整のプロセスが十分な回数繰り返されると、最終的に両者とも現在の戦略を改善することができない均衡点に到達する。この時点で、両プレイヤーは互いに最大限の搾取をしていると言える。この状態をナッシュ均衡という。
また、プレイヤーの戦略が交互に行ったり来たりして、決して均衡に収束しないことも起こりうる。この場合でも、プレイヤーの対応を少し変えることで、均衡を見出すことができる。各反復で最適な対応に全面的に切り替えるのではなく、各プレイヤーはその方向に一歩ずつ戦略を調整すればよいのです。
