
アルキメデスと放物線の面積
序.
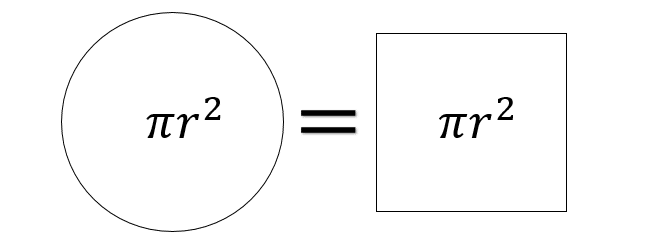
「円の正方形化」という言葉をご存じの方はいるでしょうか? 古代ギリシャでは,円と等しい面積の正方形を作図する問題が研究されていました.そしてその問題は曲線や曲面で囲まれた図形の面積や体積に等しい直線図形を作図する問題に発展しました.現在,それらの取り組みは「求積問題」と呼ばれています.
本稿では,古代ギリシャでの求積における最初の大きな成果としての,アルキメデスによる放物線の求積を,世界でもっとも分かりやすく,そして正確にお伝えします! もう一度いいます「世界でもっとも正確で分かりやすく」です.

まず積分を使って放物線の面積を確認しておきましょう.簡単に結果だけ提示しておきます.放物線を表わす関数 y=√x が囲む面積Sを「計算」します.
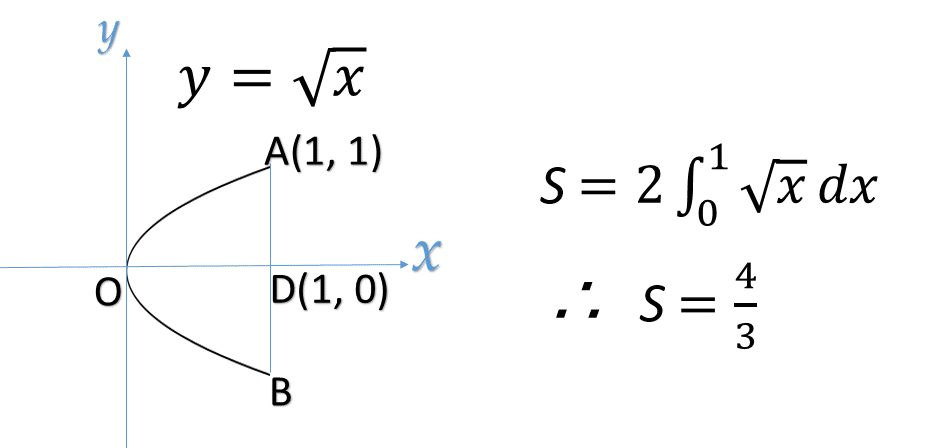
うん,一発ですね.便利な時代になりました.それではアルキメデスによる放物線の求積を始めましょう.ここで「あ!数学の話ね,私には関係ないわ」と思わず最後までお付き合いください.

「数学の分からない人はここから出て行きたまえ!」なんて事はいいませんので安心してください,出て行かなくても大丈夫です! 「世界でもっとも正確で分かりやすく」がモットーです.
1.親友の死
アルキメデスによる放物線の面積の求積は,その名も『放物線の求積』という本に収められています.この本はアルキメデスが,アレクサンドリアにいる数学者ドシテオスという(ほぼ無名の)人物に宛てた手紙です.
手紙は次のような言葉で始まります.
私たちにとって友情においては足らぬことなど何もなかったコノンが亡くなったことをお伺いし,また,貴殿がコノンと懇意であらせられ,そして幾何学に親しまれていることもお伺いし,一人の友人を亡くしただけではなく,優れた数学者までも亡くしたことを悼みまして,コノンに贈ることにしておりました幾何学の定理を書いたものを,貴殿に送ることにいたしました.
前246年以降に亡くなったとされる,サモス島生まれでアレクサンドリアの天文学者であるコノン(※友人か師匠か詳細不明)という人物の訃報が,アルキメデスの暮らすシュラクサイに届き,その返事として『放物線の求積』という手紙をしたためたのだということが分かります.この手紙は現存するアルキメデスの書簡でもっとも年代が古いものです.その後,数十年にわたって続くことになるアルキメデスとアレクサンドリアの学者との文通は衝撃的な訃報から始まるわけです.それでは数学的な内容に入りましょう.
2.放物線の性質
アルキメデスは放物線の性質を始めに確認していきます.

放物線の方程式は y=ax² と書くこともできますから,軸(y軸)の二乗が径(x軸)の二乗に比例するのは当然のことです.
しかしアルキメデスは次のように言います.「これらのことは『円錐曲線原論』にて証明されている.」
え!? 証明の必要があるのですか? しかも著者不明の本に書かれていると言っています.困りました.きっと当時はよく知られていた本なのでしょう.残念ながら失われてしまったようです.ですが安心してください,アルキメデスより年少の数学者アポロニオスという人が『円錐曲線論』という本を残してくれており,そこで証明されているのです.まず「放物線」といってもギリシャ人にとっては,円錐の母線に平行な平面による切り口が示す曲線が「放物線」なのです.アルキメデスは「直角円錐切断」と呼んでいました.

放物線の軸と径の比例関係については,アポロニオス『円錐曲線論』第Ⅰ巻命題20にて証明されています.その証明を書くにはこのnoteの余白は狭すぎるのでリンクを貼っておきます(読まなくても続きの議論には困りません)↓
なるほど,方程式がない時代,放物線というものはこのようにして作られていたのですね.
物体の軌跡を想起させる「放物線」という言い方は止めましょう.これからは「パラボラ」と呼ぶことにします.
アルキメデスはパラボラの基本的な性質がわかったところで,さらに詳しく調べていきます.パラボラ内部の線分の長さの関係を知りたいようです.
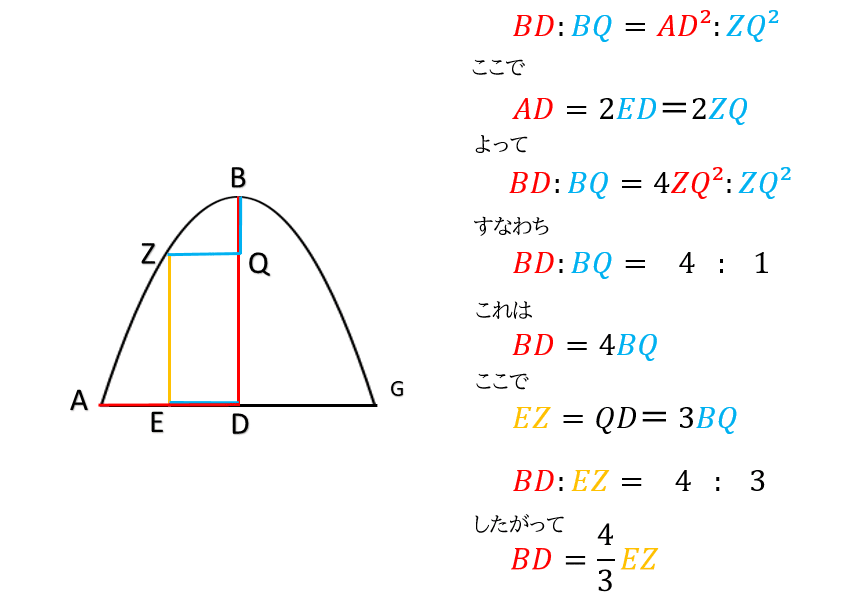
なるほど,パラボラの軸や径には整数比で表せる関係が秘められているのですね.曲線の方程式を用いなくてもこういったことが分かるのは新鮮です.

3.内接する三角形の面積
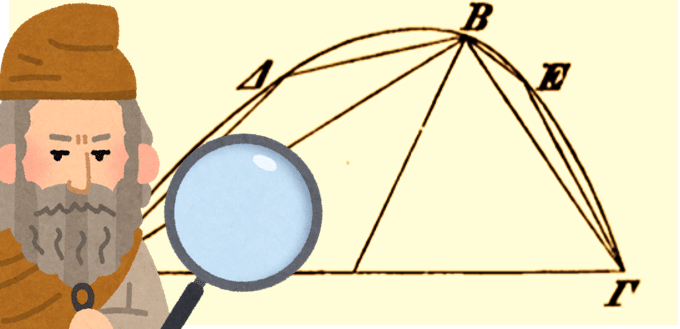
さて,パラボラの性質がわかったところで,アルキメデスは次にパラボラの内接三角形の面積を調べ始めます.
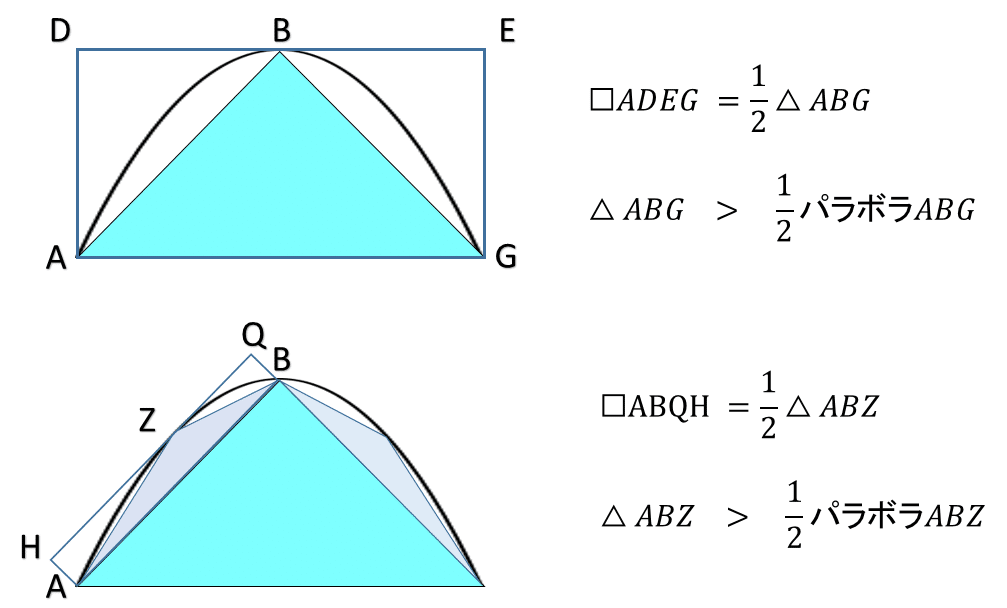
パラボラに内接する三角形の面積はパラボラの半分より大きくなるのですね.つまり次々に三角形でパラボラを埋めていくと,パラボラと内接図形の面積の差は,いくらでも小さくすることができそうです.「1/1024 より小さくできますか?」と聞かれれば「1/2048」と答えれば良いわけですね.
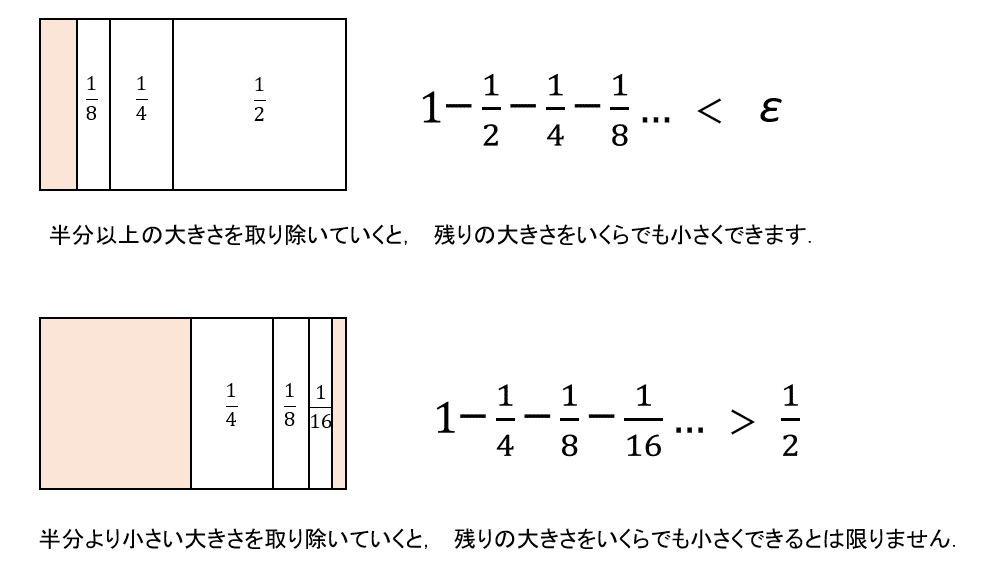
そのことが分かると,次にアルキメデスはこの内接図形の面積を足すことを思いつきます.
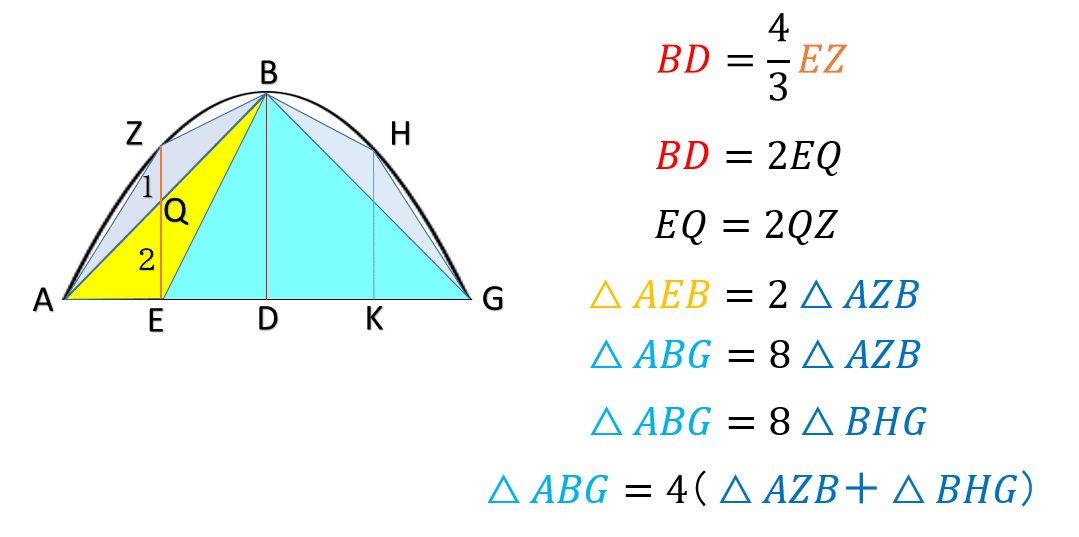
なるほど,パラボラの内接図形は,最初にできる三角形の面積を1とすれば,
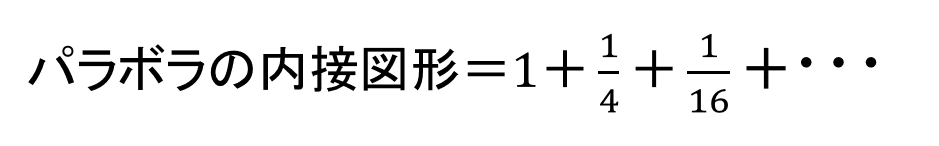
で表せるわけですね.このような関係が秘められていたとは驚きです.美しいですね!
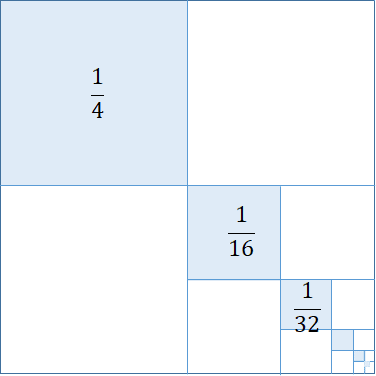
なお,この(1/4)の数列の和は上図のような正方形のタイルの敷き詰めでも理解可能です.
ですが,パラボラをいくら小さな三角形で敷き詰めていっても,ぴったりと敷き詰めることはできません.どんなに追いかけても追いつくことが出来ない,まさに「アキレウスと亀」です(→ゼノンの逆理を参照してください).

ただ,三角形を敷き詰めていくだけではダメそうです.アルキメデスはどうやって解決するのでしょうか?
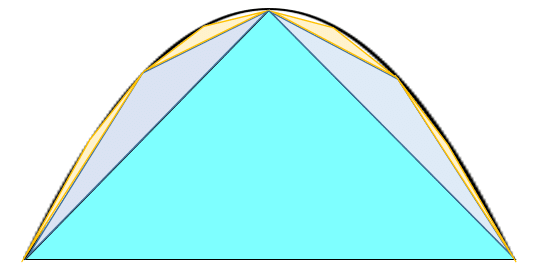
まずアルキメデスは次のような関係を発見します.
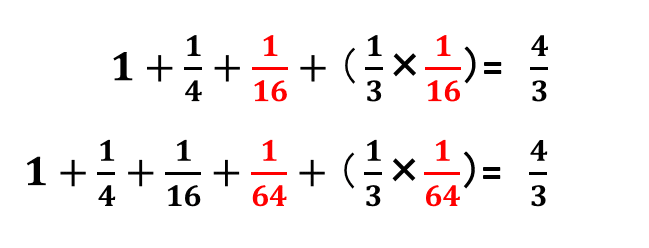
なるほど,つまり内接図形の最後の一番小さい三角形の面積の1/3倍の面積の図形を加えると,内接図形の面積はいつでも最初の三角形の4/3倍になるのですね! わくわくしてきます.それでは次にアルキメデスはどうするのでしょうか? ついにパラボラの本丸への攻撃が始まります.
4.いよいよ攻撃開始

突然,アルキメデスは「(パラボラABG)の面積は(△ABG)の4/3倍より大きいとしよう」といいます.
すると,次の関係が成り立ちます.
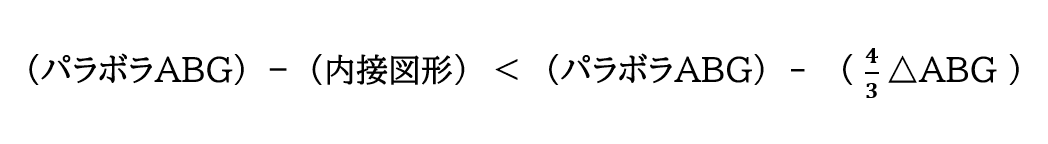
たしかに(パラボラABG)と(4/3△ABG)の面積の差がどんなに小さくても,パラボラと内接図形との差はいくらでも小さく出来るのですから,これは可能です.
A - B< A-C のとき,B>Cですよね?
すると,(内接図形)> (4/3△ABG)となります.
ちょっと待ってください! 内接図形の面積は「最後の三角形の面積の1/3倍の面積の図形を加えると,内接図形の面積はいつでも最初の三角形の4/3倍になる」のでしたよね.つまり△ABGの4/3倍より大きくなることはあり得ません.矛盾しています.するとアルキメデスはこう言います.
「格好良いです!最高です!アルキメデス先輩!」
つぎにアルキメデスはこう畳みかけます.
アルキメデス「パラボラABGの面積は△ABGの4/3倍より小さいとしよう」
アルキメデスは,パラボラに内接する三角形として十分に小さいものとしてRを作ります.つまり次のようにします.
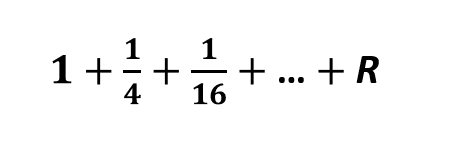
すると,(4/3△ABG)-(パラボラ)> R となる R が存在することになります.
ここで,今私たちは(4/3△ABG)>(パラボラ)と仮定しています.そして,その面積の差がどんなに小さくても,それよりも小さい面積の三角形Rを作ることができます.
ところで
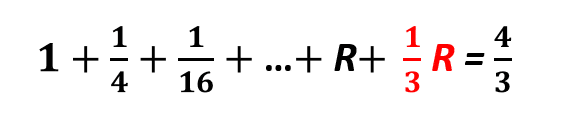
となりますよね.ところで,この関係は次のように変形できますね.
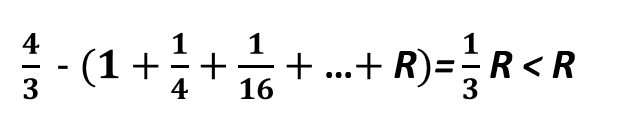
ですが私たちは(4/3△ABG)-(パラボラ)> R と仮定しています.
この二つが両立するには次の関係が成り立つ必要がありますね.
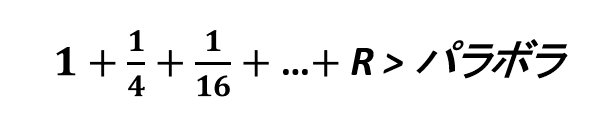
しかしこれは矛盾します.パラボラの内接図形は,パラボラよりも大きくなることは絶対にありません.当たり前ですね.ここでアルキメデスはこう告げます.
「痺れます!最高です!アルキメデスさん!その薔薇をください!」
ええと,パラボラABGの面積は,△ABGの4/3倍よりも大きくも小さくもない. つまりどうゆうことなのでしょうか? アルキメデスさん?
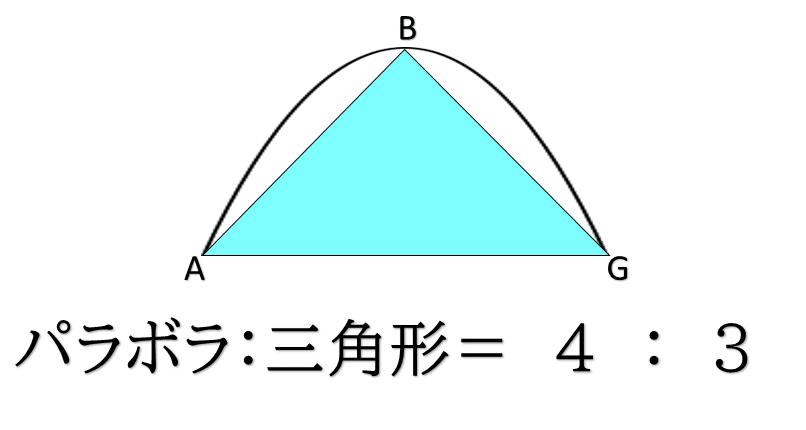
アルキメデス「パラボラの面積は内接三角形の4/3倍ということだよ」
5.おわりに
あっという間に,アルキメデスによるパラボラの求積は終わっていました.一体なにが起こったのでしょうか.
アルキメデスは,パラボラの内接図形の面積が(現代的にいえば)公比(1/4)の等比級数の和になることに注目し,さらにパラボラの面積が内接三角形の(4/3倍)より大きくても,小さくても矛盾することを証明することで,
(パラボラの面積)=4/3(内接三角形の面積)
であることを決定しました.しかし,勘の鋭い読者の方はある疑念を抱きませんでしたか?
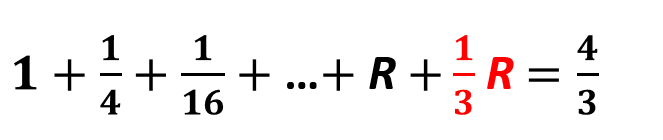
等比級数の和の公式なんてない時代です.最後に1/3を足して,4/3を導くという「出来すぎた」関係にどうやって気付いたのでしょうか? 「アルキメデスは最初から(パラボラの面積)=4/3(内接三角形の面積)であることをあらかじめ知っていたのではないのか?」という気さえしてきます.

実は,アルキメデスは証明を行う前に「ある方法」を用いることで,既にパラボラの面積を知っていたのでした.しかし,そのことが広く知られるようになったのは,アルキメデスの没後2200年ほど経った,1906年になってからだったのです.
つづく

参考文献
・斎藤憲『アルキメデス『方法』の謎を解く』岩波書店,2014年
・佐藤徹『アルキメデス 方法』東海大学出版会,1990年
・『世界の名著 9』中央公論社,1972年
・リヴィエル・ネッツ(吉田晋治 訳)『解読!アルキメデス写本』光文社,2008年
・J.L. Heiberg, Archimedis Opera Omnia Ⅱ,1880
・ R. Catesby Taliaferro /Michael N. Fried ,Conics Books I-IV ,2013
