
行列の対角化
1 対角行列
対角行列とは、対角線上の成分以外がすべて$${0}$$の正方行列をいう。
$${\begin{bmatrix} a 0 0 \\0 b 0\\0 0 c\end{bmatrix}}$$ $${\begin{bmatrix} a 0 0 0 …. \\0 b 0 0 ….\\0 0 c 0 ….\\0 0 0 e …. \\0 … … ...\end{bmatrix}}$$
2 固有値、固有ベクトル
ある$${n}$$次正方行列$${\bm{A}(=\bm{0})}$$に対して
$${\bm{Ax}=\lambda\bm{x}}$$ (1)
を満たす$${n}$$次元列ベクトル$${\bm{x}(\neq\bm{0})}$$と実数$${\lambda}$$が存在するとき、
$${\lambda}$$を$${\bm{A}}$$の固有値、$${\bm{x}}$$を$${\lambda}$$に対する固有ベクトルという。
$${n}$$次正方行列では、$${n}$$個の固有値$${\lambda_i (i=1, … ,n)}$$とそれぞれに対する固有ベクトル$${\bm{x_i}(i=1, … ,n)}$$が存在する。
一般に$${\bm{x}}$$に$${\bm{A}}$$をかけると$${\bm{Ax}}$$は様々な方向のベクトルになるが、
固有値$${\lambda}$$に対する固有ベクトル$${\bm{x}}$$のときは$${\bm{Ax}}$$と$${\bm{x}}$$は同じ方向になる。
2-1 固有値の算出
(1)$${\bm{Ax}=\lambda\bm{x}}$$ → $${\bm{Ax}-\lambda\bm{x}=\bm{0}}$$
左から単位行列$${\bm{E}}$$(対角成分が1の対角行列)をかける
$${\bm{EAx}-\bm{E}\lambda\bm{x}=\bm{0}}$$
$${\bm{Ax}-\lambda\bm{Ex}=\bm{0}}$$ → $${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$ (2)
$${\bm{x}=\bm{0}}$$なので
$${\begin{vmatrix}\bm{A}-\lambda\bm{E}\end{vmatrix}=\bm{0}}$$(固有方程式という)
これを解くと$${n}$$個の固有値($${\lambda_1, \lambda_2, … , \lambda_n }$$)が得られる。
2-2 固有ベクトルの算出
得られた$${n}$$個の固有値$${\lambda_i}$$をそれぞれ(2)に代入し
$${(\bm{A}-\lambda_i\bm{E})\bm{x_1}=\bm{0}}$$
それぞれの$${\lambda_i}$$に対応する$${n}$$個の固有ベクトル$${\bm{x_i}}$$を求める。
ちなみに、それぞれの固有ベクトル$${\bm{x_i}}$$は線形独立である。
$${c_1\bm{x_1}+c_2\bm{x_2}+ … +c_n\bm{x_n}=\bm{0}}$$
($${c_1=c_2= … +c_n=0}$$しか解を持たない)
また$${A}$$が対称行列のときは、それぞれの固有ベクトル$${\bm{x_i}}$$は直交している。
3 行列の対角化(変換行列による)
固有ベクトル$${\bm{x_i}}$$を線形結合した行列$${\bm{P}\neq\bm{0})}$$は、$${\bm{A}}$$を$${\bm{P}^-1}$$と$${\bm{P}}$$で両側からかけることで固有ベクトル$${\lambda_i}$$を対角成分とする対角行列になる。(行列の対角化。$${\bm{P}}$$を変換行列という)
$${\bm{P}=\begin{bmatrix}\bm{x_1 x_2 … x_n}\end{bmatrix}}$$ $${\bm{P}^{-1}\bm{AP}=\begin{bmatrix} \lambda_1 0 0 … \\0 \lambda_2 0 …\\0 0 \lambda_3 …\\… … …\\ … … \lambda_n\end{bmatrix}}$$
具体的な算出
3-1 $${\bm{A}=\begin{bmatrix} 3 4\\-1 -2\end{bmatrix}}$$のとき
(1)$${\bm{Ax}=\lambda\bm{x}}$$ → (2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$ → $${\begin{vmatrix}\bm{A}-\lambda\bm{E}\end{vmatrix}=\bm{0}}$$
$${\bm{A}}$$を代入
$${\begin{vmatrix} 3 4\\-1 -2\end{vmatrix}-\lambda\begin{vmatrix} 1 0\\0 1\end{vmatrix}=0}$$ → $${\begin{vmatrix}3-\lambda 4 \\-1 -2-\lambda\end{vmatrix}=0}$$
$${(3-\lambda)(-2-\lambda)-4(-1)=0}$$ → $${-6-\lambda+\lambda^2+4=0}$$
→ $${\lambda^2-\lambda-2=0}$$ → $${(\lambda-2)(\lambda+1)=0}$$
よって 固有値$${\lambda=2(=\lambda_1), -1(=\lambda_2)}$$
$${\lambda_1=2}$$のとき
$${\lambda_1}$$に対する固有ベクトルを$${\bm{x_1}=\begin{bmatrix}a_1\\a_2\end{bmatrix}}$$として
(2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$に代入
$${\Big(\begin{bmatrix} 3 4\\-1 -2\end{bmatrix}-\lambda_1\begin{bmatrix} 1 0\\0 1\end{bmatrix}\Big)\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 3-\lambda_1 4\\-1 -2-\lambda_1\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$
→ $${\begin{bmatrix} 3-2 4\\-1 -2-2\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 1 4\\-1 -4\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$
$${a_1+4a_2=0}$$ → $${a_1=4k_1, a_2=-k_1(k_1\neq0)}$$
よって、固有ベクトル$${\bm{x_1}=k_1\begin{bmatrix}4\\-1\end{bmatrix}}$$
$${\lambda_2=-1}$$のとき
$${\lambda_2}$$に対する固有ベクトルを$${\bm{x_2}=\begin{bmatrix}b_1\\b_2\end{bmatrix}}$$として
同様に(2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$に代入
$${\Big(\begin{bmatrix} 3 4\\-1 -2\end{bmatrix}-\lambda_2\begin{bmatrix} 1 0\\0 1\end{bmatrix}\Big)\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 3-\lambda_2 4\\-1 -2-\lambda_2\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$
→ $${\begin{bmatrix} 3-(-1) 4\\-1 -2-(-1)\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 4 4\\-1 -1\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$
$${b_1+4b_2=0}$$ → $${b_1=k_2, b_2=-k_2(k_2\neq0)}$$
よって、固有ベクトル$${\bm{x_2}=k_2\begin{bmatrix}1\\-1\end{bmatrix}}$$
対角化の確認
変換行列$${\bm{P}=\begin{bmatrix}\bm{x_1} \bm{x_2}\end{bmatrix}=\begin{bmatrix}\begin{bmatrix}4\\-1\end{bmatrix} \begin{bmatrix}1\\-1\end{bmatrix}\end{bmatrix}=\begin{bmatrix}4 1\\-1 -1\end{bmatrix}}$$
$${\begin{bmatrix}a b\\c d\end{bmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{bmatrix}d -b\\-c a\end{bmatrix}}$$なので
$${\bm{P}^{-1}=\dfrac{1}{4×(-1)-1×(-1)}\begin{bmatrix}-1 -1\\1 4\end{bmatrix}=-\dfrac{1}{3}\begin{bmatrix}-1 -1\\1 4\end{bmatrix}}$$
$${\bm{P}^{-1}\bm{A}\bm{P}=-\dfrac{1}{3}\begin{bmatrix}-1 -1\\1 4\end{bmatrix}\begin{bmatrix} 3 4\\-1 -2\end{bmatrix}\begin{bmatrix}4 1\\-1 -1\end{bmatrix}}$$
$${=-\dfrac{1}{3}\begin{bmatrix}-1×3-1×(-1) -1×4-1×(-2)\\1×3+4×(-1) 1×4+4×(-2)\end{bmatrix}\begin{bmatrix}4 1\\-1 -1\end{bmatrix}}$$
$${=-\dfrac{1}{3}\begin{bmatrix}-3+1 -4+2\\ 3-4 4-8\end{bmatrix}\begin{bmatrix}4 1\\-1 -1\end{bmatrix}=-\dfrac{1}{3}\begin{bmatrix}-2 -2\\-1 -4\end{bmatrix}\begin{bmatrix}4 1\\-1 -1\end{bmatrix}}$$
$${=-\dfrac{1}{3}\begin{bmatrix}-2×4-2×(-1) -2×1-2×(-1)\\-1×4-4×(-1) -1×1-4×(-1)\end{bmatrix}}$$
$${=-\dfrac{1}{3}\begin{bmatrix}-8+2 -2+2\\-4+4 -1+4\end{bmatrix}}$$
$${=-\dfrac{1}{3}\begin{bmatrix}-6 0\\ 0 3\end{bmatrix}=\begin{bmatrix}2 0\\0 -1\end{bmatrix}=\begin{bmatrix}\lambda_1 0\\ 0 \lambda_2\end{bmatrix}}$$
3-2 $${\bm{A}=\begin{bmatrix} 2 2\\2 -1\end{bmatrix}}$$(対称行列)のとき
(1)$${\bm{Ax}=\lambda\bm{x}}$$ → (2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$ → $${\begin{vmatrix}\bm{A}-\lambda\bm{E}\end{vmatrix}=\bm{0}}$$
$${\bm{A}}$$を代入
$${\begin{vmatrix}2-\lambda 2 \\2 -1-\lambda\end{vmatrix}=0}$$
$${(2-\lambda)(-1-\lambda)-2×2=0}$$ → $${-2-\lambda+\lambda^2-4=0}$$
→ $${\lambda^2-\lambda-6=0}$$ → $${(\lambda-3)(\lambda+2)=0}$$
よって 固有値$${\lambda=3(=\lambda_1), -2(=\lambda_2)}$$
$${\lambda_1=3}$$のとき
$${\lambda_1}$$に対する固有ベクトルを$${\bm{x_1}=\begin{bmatrix}a_1\\a_2\end{bmatrix}}$$として
(2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$に代入
$${\begin{bmatrix}2-\lambda_1 2 \\ 2 -1-\lambda_1\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 2-3 2\\2 -1-3\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$
→ $${\begin{bmatrix}-1 2\\2 -4\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\bm{0}}$$
$${-a_1+2a_2=0}$$ → $${a_1=2k_1, a_2=k_1(k_1\neq0)}$$
よって、固有ベクトル$${\bm{x_1}=k_1\begin{bmatrix}2\\1\end{bmatrix}}$$
$${\lambda_2=-2}$$のとき
$${\lambda_2}$$に対する固有ベクトルを$${\bm{x_2}=\begin{bmatrix}b_1\\b_2\end{bmatrix}}$$として
同様に(2)$${(\bm{A}-\lambda\bm{E})\bm{x}=\bm{0}}$$に代入
$${\begin{bmatrix} 2-\lambda_2 2 \\ 2 -1-\lambda_2\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$ → $${\begin{bmatrix} 2-(-2) 2\\2 -1-(-2)\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$
→ $${\begin{bmatrix}4 2\\2 1\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=\bm{0}}$$
$${4b_1+2b_2=0}$$ → $${b_1=k_2, b_2=-2k_2(k_2\neq0)}$$
よって、固有ベクトル$${\bm{x_2}=k_2\begin{bmatrix}1\\-2\end{bmatrix}}$$
※2つの固有ベクトル$${\bm{x_1}=k_1\begin{bmatrix}2\\1\end{bmatrix}}$$、$${\bm{x_2}=k_2\begin{bmatrix}1\\-2\end{bmatrix}}$$ は$${\underline{直交している}}$$。
対角化の確認
変換行列$${\bm{P}=\begin{bmatrix}\bm{x_1} \bm{x_2}\end{bmatrix}=\begin{bmatrix}2 1\\1 -2\end{bmatrix}}$$
$${\bm{P}^{-1}=\dfrac{1}{2×(-2)-1×1}\begin{bmatrix}-2 -1\\-1 2\end{bmatrix}=\dfrac{1}{5}\begin{bmatrix}2 1\\1 -2\end{bmatrix}}$$
$${\bm{P}^{-1}\bm{A}\bm{P}=\dfrac{1}{5}\begin{bmatrix}2 1\\1 -2\end{bmatrix}\begin{bmatrix}2 2\\2 -1\end{bmatrix}\begin{bmatrix}2 1\\1 -2\end{bmatrix}}$$
$${=\dfrac{1}{5}\begin{bmatrix}4+2 4-1\\2-4 2+2\end{bmatrix}\begin{bmatrix}2 1\\1 -2\end{bmatrix}=\dfrac{1}{5}\begin{bmatrix} 6 3\\-2 4\end{bmatrix}\begin{bmatrix}2 1\\1 -2\end{bmatrix}}$$
$${=\dfrac{1}{5}\begin{bmatrix}12+3 6-6\\-4+4 -2-8\end{bmatrix}=\dfrac{1}{5}\begin{bmatrix}15 0\\ 0 -10\end{bmatrix}=\begin{bmatrix}3 0\\0 -2\end{bmatrix}=\begin{bmatrix}\lambda_1 0\\ 0 \lambda_2\end{bmatrix}}$$
4 対称行列の対角化(直交行列による)
直交行列によっても対称行列は対角化できる。
このほうが手数が多いが、主軸変換(主軸の回転)に必要な方法である。
4-1 前置き
対称行列
行と列を入れ替えた正方行列を転置行列といい
対称行列はその行列は転置行列と等しい。
$${\bm{A}=^t\bm{A}}$$ (3)
直交行列
転置行列と逆行列が等しい行列を直交行列という。
$${^t \bm{U}=\bm{U}^{-1}}$$ (4)
正規化
ベクトルの長さを1にすることをベクトルの正規化という。
具体的には、ベクトルをその長さで割る。
$${\bm{u}=\dfrac{\bm{x}}{\|x\|}}$$ (3) ただし、$${\|x\|=\sqrt{\sum {x_i}^2}}$$
4-2 手順
対称行列$${\bm{A}}$$を対角化する。
まず3の手順に従って固有値$${\lambda_i}$$と固有ベクトル$${\bm{x_i}}$$を求める。
固有ベクトルを正規化する。
$${\bm{u_i}=\dfrac{1}{\|x_i\|}\bm{x_i}}$$
直交行列$${U}$$(正規化された変換ベクトル)を求める。
$${\bm{U}=\begin{bmatrix}\bm{u_1} \bm{u_2} … \bm{u_n}\end{bmatrix}}$$
$${\bm{U}^{-1}=^t\bm{U}}$$
対角化する
$${\bm{U}^{-1}\bm{A}\bm{U}=^t\bm{U}\bm{A}\bm{U}= … =\begin{bmatrix} \lambda_1 0 0 … \\0 \lambda_2 0 …\\0 0 \lambda_3 …\\… … …\\ … … \lambda_n\end{bmatrix}}$$
4-3 具体的な算出
$${\bm{A}=\begin{bmatrix}3 2\\2 3\end{bmatrix}}$$を対角化する。
固有値を求める。
$${\bm{A}\bm{x}=\lambda\bm{Ex}}$$
$${\begin{bmatrix}3-\lambda 2\\2 3-\lambda\end{bmatrix}\bm{x}=\bm{0}}$$ → $${(3-\lambda)^2-2^2=0}$$ → $${(5-\lambda)(1-\lambda)=0}$$
$${\lambda=1(=\lambda_1), 5(=\lambda_2)}$$
固有ベクトルを求める。
$${\lambda=1(=\lambda_1)}$$のとき
$${\begin{bmatrix}3-1 2\\2 3-1\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=0}$$ → $${2a_1+2a_2=0}$$ → $${\bm{x_1}=k_1\begin{bmatrix}1\\-1\end{bmatrix}}$$
正規化すると $${\bm{u_1}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1\\-1\end{bmatrix}}$$
$${\lambda=5(=\lambda_2)}$$のとき
$${\begin{bmatrix}3-5 2\\2 3-5\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=0}$$ → $${-2b_1+2b_2=0}$$ → $${\bm{x_2}=k_2\begin{bmatrix}1\\1\end{bmatrix}}$$
正規化すると $${\bm{u_2}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1\\1\end{bmatrix}}$$
直交化行列$${\bm{U}}$$を求める。
$${\bm{U}=\dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 1\\-1 1\end{bmatrix}}$$
$${\bm{U}^{-1}= ^t\bm{U}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1 -1\\1 1\end{bmatrix}}$$
$${\bm{A}}$$を対角化する。
$${^t\bm{U}\bm{A}\bm{U}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1 -1\\1 1\end{bmatrix}\begin{bmatrix}3 2\\2 3\end{bmatrix}\dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 1\\-1 1\end{bmatrix}}$$
$${=\dfrac{1}{2}\begin{bmatrix}3-2 2-3\\3+2 2+3\end{bmatrix}\begin{bmatrix} 1 1\\-1 1\end{bmatrix}=\dfrac{1}{2}\begin{bmatrix}1 -1\\5 5\end{bmatrix}\begin{bmatrix} 1 1\\-1 1\end{bmatrix}}$$
$${=\dfrac{1}{2}\begin{bmatrix}1+1 1-1\\5-5 5+5\end{bmatrix}=\dfrac{1}{2}\begin{bmatrix}2 0\\0 10\end{bmatrix}=\begin{bmatrix}1 0\\0 5\end{bmatrix}=\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}}$$
5 主軸変換
$${3x^2+4xy+3y^2=5}$$のグラフは多分傾いた楕円である。
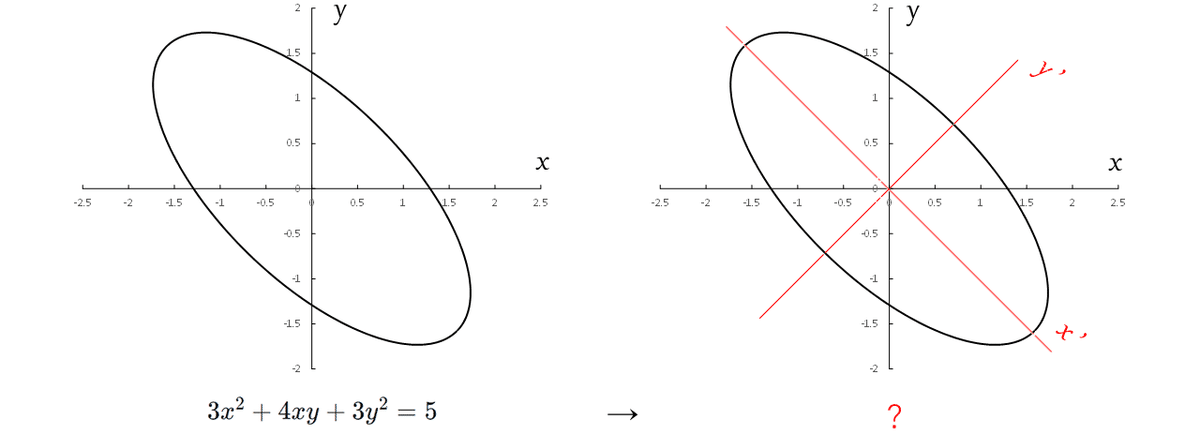
座標系Oーxyでの記述$${3x^2+4xy+3y^2=0}$$を楕円の長軸と短軸を通る
新しい座標系Ox'y'の記述への変換を考える。
まず$${3x^2+4xy+3y^2=5}$$の左辺を対称行列を用いた形に変形する。
$${3x^2+4xy+3y^2=\begin{bmatrix}x y\end{bmatrix}\begin{bmatrix}a c\\c b\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}}$$
$${=\begin{bmatrix}ax+cy cx+by\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}ax^2+2cxy+by^2\end{bmatrix}}$$
よって $${a=3, b=3, c=2}$$
$${3x^2+4xy+3y^2=\begin{bmatrix}x y\end{bmatrix}\begin{bmatrix}3 2\\2 3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}}$$
$${\bm{A}=\begin{bmatrix}3 2\\2 3\end{bmatrix}}$$とし対角化を行う。
4-2の結果より
固有値$${\lambda_1=1, \lambda_2=5}$$
変換(直交)行列$${\bm{U}=\dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 1\\-1 1\end{bmatrix}}$$ $${\bm{U}^{-1}= ^t\bm{U}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1 -1\\1 1\end{bmatrix}}$$
対角化の結果は
$${^t\bm{UAU}^{-1}=^t\bm{U}\begin{bmatrix}3 2\\2 3\end{bmatrix}\bm{U}^{-1}=\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}=\begin{bmatrix}1 0\\0 5\end{bmatrix}}$$ (5)
また
$${\begin{bmatrix}x\\y\end{bmatrix}=\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}}$$ (6) $${\begin{bmatrix}x y\end{bmatrix}=^t\begin{bmatrix}x\\y\end{bmatrix}}$$ (7)
$${3x^2+4xy+3y^2=5}$$ → $${\begin{bmatrix}x y\end{bmatrix}\begin{bmatrix}3 2\\2 3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=5}$$
(6)(7)を代入
$${^t\begin{bmatrix}x\\y\end{bmatrix}\begin{bmatrix}3 2\\2 3\end{bmatrix}\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$
(6)を代入
$${^t\begin{Bmatrix}\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}\end{Bmatrix} \begin{bmatrix}3 2\\2 3\end{bmatrix}\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$ → $${^t\begin{bmatrix}x'\\y'\end{bmatrix} ^t\bm{U}\begin{bmatrix}3 2\\2 3\end{bmatrix}\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$
$${\begin{bmatrix}x' y'\end{bmatrix} ^t\bm{U}\begin{bmatrix}3 2\\2 3\end{bmatrix}\bm{U}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$
(5)を代入
$${\begin{bmatrix}x' y'\end{bmatrix}\begin{bmatrix}1 0\\0 5\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$ → $${\begin{bmatrix}x'+0 0+5y'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}=5}$$
$${x'^2+5y'^2=5}$$
よって
$${\Big(\dfrac{x'}{\sqrt{5}}\Big)^2+\Big(\dfrac{y'}{1}\Big)^2=1}$$
$${x'}$$軸を長軸$${\sqrt{5}}$$、$${y'}$$軸を短軸$${1}$$とする楕円である。
また(6)より
$${\begin{bmatrix}x'\\y'\end{bmatrix}=\bm{U}^{-1}\begin{bmatrix}x\\y\end{bmatrix}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1 -1\\1 1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}\dfrac{1}{\sqrt{2}} -\dfrac{1}{\sqrt{2}}\\\dfrac{1}{\sqrt{2}} \dfrac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}}$$
$${=\begin{bmatrix} \cos(-45^\circ) \sin(-45^\circ)\\-\sin(-45^\circ) \cos(-45^\circ) \end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}}$$
座標系O-x'y'は、座標系O-xyを時計回りに45°回転させたものである。

この記事が気に入ったらサポートをしてみませんか?
