
単振動の正準変換
正準変換の例として単振動からの変換があげられることが多い。
それらについての正準変換とトラジェクトリーを考えた。
0 単振動の式
以前に書いた位相空間、トラジェクトリーの3より
$${q=q_0\cos\sqrt{\dfrac{k}{m}} t=q_0\cos\omega t}$$ (0-q)
$${p=-mq_0\sqrt{\dfrac{k}{m}}\sin\sqrt{\dfrac{k}{m}} t=-mq_0\omega\sin\omega t}$$ (0-p)
$${\mathscr{H}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}}$$ (0-H)
$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(q_0\sqrt{mk})^2}=1}$$ または$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$ (0-q-p)
Hamilton's eq
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}=-q_0\sqrt{\dfrac{k}{m}}\sin\sqrt{\dfrac{k}{m}} t=-q_0\omega\sin\omega t}$$ (0-q')
$${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=-kq=ーkq_0\cos\sqrt{\dfrac{k}{m}} t=ーkq_0\cos\omega t}$$ (0-p')
トラジェクトリーは
$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$ (0-q-p)
$${q_o, mq_0\omega}$$を各径とする楕円、$${(q_0,0)}$$を起点として時計回りに移動

1 恒等変換
0から以下の変換を考える。
$${P=p, Q=q}$$ → $${p=P, q=Q}$$
まったく変化のない変換である。それゆえ恒等変換という。
(0-H)(0-q-p)に代入
$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{kQ^2}{2}}$$ (1-H)
トラジェクトリーは
$${\dfrac{Q^2}{q_0^2}+\dfrac{P^2}{(mq_0\omega)^2}=1}$$ (1-q-p)
$${q_o, mq_0\omega}$$を各径とする楕円、$${(q_0,0)}$$を起点として時計回りに移動
2 円への変換
1のトラジェクトリーが楕円から円になるように変換をおこなう。
1の楕円の面積$${S=\pi×q_0×mq_0\omega=\pi mq_0^2}$$
変換後の円の半径を$${r}$$とすると
$${\pi r^2=mq_0^2\pi}$$ よって$${r=q_0\sqrt{m\omega}}$$
トラジェクトリーは
$${\dfrac{Q^2}{q_0^2m\omega}+\dfrac{P^2}{q_0^2m\omega}=1}$$ (2-Q-P) となる。(始点$${(q_0\sqrt{m\omega}, 0)}$$)
(0-q-p)と比較して変換の式を求める
$${\dfrac{q^2}{q_0^2}=\dfrac{Q^2}{q_0^2m\omega}, Q^2=\sqrt{m\omega} q^2, Q=\sqrt{m\omega} q}$$ (2-Q)
$${\dfrac{p^2}{(mq_0\omega)^2}=\dfrac{P^2}{q_0^2m\omega}, P^2=\dfrac{q_0^2m\omega}{m^2q_0^2\omega^2}p^2=\dfrac{1}{m\omega}p^2, P=\dfrac{1}{\sqrt{m\omega}}p}$$ (2-P)

では、この変換が Hamilton の正準方程式を満たすかを確認する。
(2-Q)(2-P)より
$${q=(m\omega)^{-1/2}Q}$$ (2-q) $${p=(m\omega)^{1/2}P}$$ (2-p)
(0-H)に代入
$${\mathscr{\overline{H}}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}}$$
$${=\dfrac{((m\omega)^{1/2}P)^2}{2m}+\dfrac{k((m\omega)^{-1/2}Q)^2}{2}=\dfrac{m\omega P^2}{2m}+\dfrac{(km^{-1})\omega^{-1}Q^2}{2}}$$
$${=\dfrac{\omega P^2}{2}+\dfrac{\omega^2\omega^{-1}Q^2}{2}=\dfrac{\omega}{2}(P^2+Q^2)}$$ (2-H')
$${\dot{Q}}$$について
(2-Q)$${Q=\sqrt{m\omega} q}$$より
$${\dot{Q}=\sqrt{m\omega} \dot{q}}$$ ←(0-q')$${\dot{q}=\dfrac{p}{m}}$$を代入
$${=\sqrt{m\omega}\dfrac{p}{m}=\sqrt{\dfrac{\omega}{m}} p}$$ (○)
(2-H')$${\mathscr{\overline{H}}=\dfrac{\omega}{2}(P^2+Q^2)}$$より
$${\dot{Q}=\dfrac{dQ}{dt}=\dfrac{\partial\mathscr{\overline{H}}}{\partial P}=\omega P}$$ ←(2-P)$${P=\dfrac{1}{\sqrt{m\omega}}p}$$を代入
$${=\omega \dfrac{1}{\sqrt{m\omega}}=\sqrt{\dfrac{\omega}{m}} p}$$ (◇)
よって ○=◇
$${\dot{P}}$$について
(2-P)$${P=\dfrac{1}{\sqrt{m\omega}}p}$$より
$${\dot{P}=\dfrac{1}{\sqrt{m\omega}}\dot{p}}$$ ←(0-p')$${\dot{p}=-kq}$$ を代入
$${=\dfrac{-kq}{\sqrt{m\omega}}}$$ ←$${\omega^2=\dfrac{k}{m}, k=m\omega^2}$$
$${=-\dfrac{m\omega^2}{\sqrt{m\omega}}q=-\sqrt{m\omega^3} q}$$ (□)
(2-H')$${\mathscr{\overline{H}}=\dfrac{\omega}{2}(P^2+Q^2)}$$より
$${\dot{P}=\dfrac{dP}{dt}=-\dfrac{\partial\mathscr{\overline{H}}}{\partial Q}=\omega Q}$$ ←(2-Q)$${Q=\sqrt{m\omega} q}$$を代入
$${=\omega \sqrt{m\omega} q=\sqrt{m\omega^3} q}$$ (△)
よって (□)=(△)
というわけでHamiltonの正準方程式は成り立つ。
3 直線への変換
2から以下の変換を考える。Poincaré 変換という。
$${q=\sqrt{2P}\sin Q}$$ (3-q)
$${p=\sqrt{2P}\cos Q}$$ (3-p)
まず$${Q, P}$$を求めておく。
(3-q)÷(3-p)
$${\dfrac{q}{p}=\dfrac{\sin Q}{\cos Q}=\tan Q, Q=\tan^{-1}\dfrac{q}{p}}$$ (3-Q)
(3-q)^2+(3-p)^2
$${q^2+p^2=2P, P=\dfrac{q^2+p^2}{2}}$$ (3-P)
では、この変換がHamiltonの正準方程式を満たすかを確認するが、その前に混乱を避けるために(2-H')の$${Q,P,\mathscr{\overline{H}}}$$を$${q,p,\mathscr{H}}$$に入れ替えておく。
$${\mathscr{H}=\dfrac{\omega}{2}(p^2+q^2)}$$ (2-H)
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\omega p}$$ (2-q')
$${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=-\omega q}$$ (2-p')
(2-H)に(3-q)(3-p)を代入
$${\mathscr{\overline{H}}=\dfrac{\omega}{2}(p^2+q^2)=\dfrac{\omega}{2}((\sqrt{2P}\cos Q)^2+(\sqrt{2{P}}\sin{Q})^2)}$$
$${=\dfrac{\omega}{2}2P(\cos^2 Q+\sin^2{Q})=\omega P}$$ (3-H)
では$${\dot{Q}}$$について
(3-Q)$${Q=\tan^{-1}\dfrac{q}{p}}$$より
$${\dot{Q}=\dfrac{1}{1+\Big(\dfrac{q}{p}\Big)^2}\dfrac{d}{dt}\Big(\dfrac{q}{p}\Big)=\dfrac{p^2}{q^2+p^2}\dfrac{d}{dt}(qp^{-1})=\dfrac{p^2}{q^2+p^2}(\dot{q}p^{-1}-qp^{-2}\dot{p})}$$
$${=\dfrac{p^2}{q^2+p^2}\Big(\dfrac{\dot{q}}{p}-\dfrac{q\dot{p}}{p^2}\Big)=\dfrac{p^2}{q^2+p^2}\dfrac{\dot{q}p-q\dot{p}}{p^2}=\dfrac{\dot{q}p-q\dot{p}}{q^2+p^2}}$$←(2-q')(2-p')を代入
$${=\dfrac{\omega p p-q(-\omega q)} {q^2+p^2}=\dfrac{\omega(q^2+p^2)}{q^2+p^2}=\omega}$$ (■)
(3-H)$${\mathscr{\overline{H}}=\omega P}$$より
$${\dot{Q}=\dfrac{dQ}{dt}=\dfrac{\partial\mathscr{\overline{H}}}{\partial P}=\omega}$$ (▲) よって (■) =(▲)
(3-P)$${P=\dfrac{q^2+p^2}{2}}$$より
$${\dot{P}=\dfrac{2q\dot{q}+2p\dot{p}}{2}=q\dot{q}+p\dot{p}}$$←(2-q')(2-p')を代入
$${=q(\omega p)+p(-\omega q)=0}$$ (●)
(3-H)$${\mathscr{\overline{H}}=\omega P}$$より
$${\dot{P}=\dfrac{dP}{dt}=-\dfrac{\mathscr{\partial\overline{H}}}{\partial Q}=0}$$ (◆) よって(●)=(◆)
というわけでHamiltonの正準方程式は成り立つ。
トラジェクトリーは
初期条件$${t=0, q=q_0\sqrt{m\omega}, p=0}$$(始点)より
(3-P)$${P=\dfrac{q^2+p^2}{2}=\dfrac{(q_0\sqrt{m\omega})^2+0}{2}=\dfrac{q_0^2m\omega}{2}}$$
(3-Q)$${Q=\tan^{-1}\dfrac{q}{p}=\tan^{-1}\dfrac{q_0\sqrt{m\omega}}{0}=\infty?}$$
これでは$${Q}$$が出ないのでこの式の元の(3-q)(3-p)を使う。
それぞれに$${P}$$と$${q=q_0\sqrt{m\omega}, p=0}$$を代入する。
(3-q)$${q=\sqrt{2P}\sin Q}$$
$${q_0\sqrt{m\omega}=\sqrt{2\dfrac{q_0^2m\omega}{2}}\sin Q=q_0\sqrt{m\omega}\sin Q, \sin Q=1}$$ (3-q-s)
(3-p)$${p=\sqrt{2P}\cos Q}$$
$${0=\sqrt{2\dfrac{q_0^2m\omega}{2}}\cos Q, \cos Q=0}$$ (3-p-c)
よって(3-q-s)(3-p-c)を満たす $${Q=\dfrac{\pi}{4}}$$
まとめると初期条件($${t-0, Q=\dfrac{\pi}{4}, P=\dfrac{q_0^2m\omega}{2}}$$)
(■)$${\dot{Q}=\omega}$$より
$${Q=\omega t+C_1, \dfrac{\pi}{4}=0+C_1, C_1=\dfrac{\pi}{4}}$$ よって$${Q=\omega t+\dfrac{\pi}{4}}$$
(●)$${\dot{P}=q(\omega p)+p(-\omega q)=0}$$より
$${P=C_2=\dfrac{q_0^2m\omega}{2}}$$ よって$${P=\dfrac{q_0^2m\omega}{2}}$$

4 P=p, Q=q-p
0からの変換を考える。
$${P=p}$$ (4-P) $${p=P}$$ (4-p)
$${Q=q-p}$$ (4-Q) $${q=Q+p=Q+P}$$ (4-q)
(0-H)$${\mathscr{{H}}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}}$$より
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}}$$ (4-q') $${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=-kq}$$ (4-p')
(4-p)(4-q)を(0-H)に代入
$${\mathscr{\overline{H}}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}=\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}}$$ (4-H)
Hamiltonの正準方程式を満たすかを確認する。
$${\dot{Q}}$$について
(4-Q)$${Q=q-p}$$より
$${\dot{Q}=\dot{q}-\dot{p}}$$ ←(4-q')(4-p')を代入
$${=\dfrac{p}{m}+kq}$$ (▽)
(4-H)$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}}$$より
$${\dot{Q}=\dfrac{dQ}{dt}=\dfrac{\partial\mathscr{\overline{H}}}{\partial P}=\dfrac{2P}{2m}+\dfrac{2k(Q+P)}{2}}$$ ←(4-q)$${q=Q+P}$$, (4-P)$${P=p}$$
$${=\dfrac{p}{m}+kq}$$ (△) よって(▽)=(△)
$${\dot{P}}$$について
(4-P)$${P=p}$$より
$${\dot{P}=\dot{p}=-kq}$$(◎) ←(4-p')$${\dot{p}=-kq}$$
(4-H)$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}}$$より
$${\dot{P}=\dfrac{dP}{dt}=-\dfrac{\partial\mathscr{\overline{H}}}{\partial Q}=-\dfrac{2k(Q+P)}{2}=-kq}$$(▣) ←(4-q)$${q=Q+P}$$
よって(◎)=(▣)
というわけでHamiltonの正準方程式は成り立つ。
ではトラジェクトリーを考える。
$${q=q_0\cos\omega t}$$ (0-q) ($${\omega=\sqrt{k/m}}$$ )
$${p=-mq_0\omega\sin\omega t}$$ (0-p)
$${\mathscr{H}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}}$$ (0-H)
$${\dot{q}=\dfrac{p}{m}}$$ (0-q') $${\dot{p}=-kq}$$ (0-p')
$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$ (0-q-p) 起点$${(q_0,0)}$$
初期条件$${t=0, q=q_0, p=0}$$(始点)より
(4-Q)$${Q=q-p=q_0-0=q_0}$$ (4-P)$${P=p=0}$$
よって4での初期条件$${t=0, Q=q_0, P=0}$$ 始点$${(q_0, 0)}$$
これを(4-H)に代入すると
$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}=\dfrac{0}{2m}+\dfrac{k(q_0+0)^2}{2}=\dfrac{kq_0^2}{2}}$$
よって、トラジェクトリーは
$${\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}=\dfrac{kq_0^2}{2}}$$ (4-T) 起点$${(q_0, 0)}$$ である。
式の形から2次曲線であることがわかる。
どんな形かをはっきりさせるために主軸変換をおこなう。
やり方は2次曲線、主軸変換に従うことにする。
(4-T)の両辺に$${2m}$$をかける。
$${P^2+mk(Q+P)^2=mkq_0^2}$$
$${P^2+mkQ^2+2mkQP+mkP^2-mkq_0^2=0}$$
$${mkQ^2+2mkQP+(mk+1)P^2-mkq_0^2=0}$$ (2-T')
2次曲線、主軸変換の1によると
$${ax^2+bxy+cy^2+dx+ey+f=0}$$
$${b^2-4ac<0}$$のとき 楕円
$${b^2-4ac>0}$$のとき 双曲線
$${b^2-4ac=0}$$のとき 放物線 である。
これを(2-T')にあてはめると
$${a=mk, b=2mk, c=mk+1, d=e=0, f=-mkq_0^2}$$
$${b^2-4ac=(2mk)^2-4mk(mk+1)=4m^2k^2-4m^2k^2-4mk}$$
$${=-4mk<0}$$ となり、(2-T')は楕円である。$${(m>0, k>0)}$$
(2-T')を更に変形して
$${mkQ^2+mkQP+mkQP+(mk+1)P^2-mkq_0^2=0}$$
$${(mkQ+mkP)Q+\{mkQ+(mk+1)P\}P-mkq_0^2=0}$$
$${\begin{bmatrix}Q P\end{bmatrix}\begin{bmatrix}mkQ+mkP\\mkQ+(mk+1)\end{bmatrix}-mkq_0^2=0}$$
$${\begin{bmatrix}Q P\end{bmatrix}\begin{bmatrix}mk mk \\mk mk+1\end{bmatrix}\begin{bmatrix}Q\\P\end{bmatrix}-mkq_0^2=0}$$ (2-T'')
(以下、2次曲線、主軸変換2に従って進める)
$${\bm{A}=\begin{bmatrix}mk mk \\mk mk+1\end{bmatrix}}$$とし、$${\bm{A}}$$の固有値を$${\lambda}$$、固有ベクトルを$${\bm{x}}$$とする。
$${\bm{Ax}=\lambda\bm{x}}$$ ← 両辺の左から$${\bm{E}}$$を掛ける。
$${\bm{EAx}=\lambda\bm{Ex}, (\bm{A}-\lambda\bm{E})\bm{x}=0}$$
$${ \Big(\begin{bmatrix}mk mk \\mk mk+1\end{bmatrix}-\begin{bmatrix}\lambda 0\\0 \lambda\end{bmatrix}\Big)\bm{x}=0,}$$ $${\begin{bmatrix}mk-\lambda mk\\mk mk+1-\lambda\end{bmatrix}\bm{x}=0}$$
$${\begin{vmatrix}mk-\lambda mk\\mk mk+1-\lambda\end{vmatrix}=0}$$
$${(mk-\lambda)(mk+1-\lambda)-m^2k^2=0}$$
$${(mk-\lambda)^2+mk-\lambda-m^2k^2=0}$$
$${\lambda^2-2mk\lambda+m^2k^2+mk-\lambda-m^2k^2=0}$$
$${\lambda^2-(2mk+1)\lambda+mk=0}$$
$${\lambda=\dfrac{2mk+1\pm\sqrt{(2mk+1)^2-4mk}}{2}=\dfrac{2mk+1\pm\sqrt{4m^2k^2+1}}{2}}$$
$${\lambda_1=\dfrac{2mk+1+\sqrt{4m^2k^2+1}}{2}, \lambda_2=\dfrac{2mk+1-\sqrt{4m^2k^2+1}}{2}}$$
$${\bm{P}}$$:$${\lambda_1,\lambda_2}$$から得られる対角化ベクトル
$${\bm{P}=\begin{bmatrix}\cos\theta -\sin\theta\\\sin\theta \cos\theta\end{bmatrix}}$$
$${\theta=\dfrac{1}{2}\tan^{-1}\Big(\dfrac{b}{a-c}\Big)=\dfrac{1}{2}\tan^{-1}\Big(\dfrac{(mk)}{(mk)-(mk+1)}\Big)}$$
$${=\dfrac{1}{2}\tan^{-1}(-mk)=-\dfrac{1}{2}\tan^{-1}(mk)<0 (m>0, k>0)}$$
$${ ^t\bm{P}}$$:$${\bm{P}}$$の転置ベクトル とすると
$${\begin{bmatrix}Q\\P\end{bmatrix}=\bm{P}\begin{bmatrix}Q'\\P'\end{bmatrix}, \begin{bmatrix}Q'\\P'\end{bmatrix}= ^t\bm{P}\begin{bmatrix}Q\\P\end{bmatrix}, ^t\bm{PAP}=\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}}$$
(2-T'')は
$${\begin{bmatrix}Q P\end{bmatrix}\bm{A}\begin{bmatrix}Q\\P\end{bmatrix}-mkq_0^2=0}$$ $${\begin{matrix}\\ \end{matrix}^t\begin{bmatrix}Q\\P\end{bmatrix}\bm{A}\begin{bmatrix}Q\\P\end{bmatrix}-mkq_0^2=0}$$
$${\begin{matrix}\\ \end{matrix}^t\Big\{\bm{P}\begin{bmatrix}Q'\\P'\end{bmatrix}\Big\}\bm{A}\bm{P}\begin{bmatrix}Q'\\P'\end{bmatrix}-mkq_0^2=0}$$ $${\begin{matrix}\\ \end{matrix}^t\begin{bmatrix}Q'\\P'\end{bmatrix} ^t\bm{P}\bm{A}\bm{P}\begin{bmatrix}Q'\\P'\end{bmatrix}-mkq_0^2=0}$$
$${\begin{bmatrix}Q' P'\end{bmatrix}\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}\begin{bmatrix}Q'\\P'\end{bmatrix}-mkq_0^2=0}$$ $${\begin{bmatrix}\lambda_1Q' \lambda_2P'\end{bmatrix}\begin{bmatrix}Q'\\P'\end{bmatrix}-mkq_0^2=0}$$
$${\lambda_1Q'^2+\lambda_2P'^2-mkq_0^2=0}$$ $${\lambda_1Q'^2+\lambda_2P'^2=mkq_0^2}$$
$${\dfrac{Q'^2}{ \dfrac{mkq_0^2}{\lambda_1} }+\dfrac{P'^2}{ \dfrac{mkq_0^2}{\lambda_2} }=1}$$ (4-T")
長くなった。まとめる。
座標系O-QPにおいては
$${\dfrac{P^2}{2m}+\dfrac{k(Q+P)^2}{2}=\dfrac{kq_0^2}{2}}$$ (4-T) 起点$${(q_0, 0)}$$
座標系O-Q'P'においては
座標系O-QPから$${\theta(=-\dfrac{1}{2}\tan^{-1}(mk))}$$回転した座標系
$${\dfrac{Q'^2}{ \dfrac{mkq_0^2}{\lambda_1} }+\dfrac{P'^2}{ \dfrac{mkq_0^2}{\lambda_2} }=1}$$ (4-T")
Q'軸方向の径$${\sqrt{\dfrac{mkq_0^2}{\lambda_1}}}$$、P'軸方向の径$${\sqrt{\dfrac{mkq_0^2}{\lambda_2}}}$$とする楕円
$${\lambda_1=\dfrac{2mk+1+\sqrt{4m^2k^2+1}}{2}, \lambda_2=\dfrac{2mk+1-\sqrt{4m^2k^2+1}}{2}}$$

最後に正準変換前後の楕円の面積が等しいことを確認しておく。
変換前 $${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$ (0-q-p)
$${S=\pi\sqrt{q_0^2}\sqrt{(mq_0\omega)^2}=\pi q_0^2m\omega=\pi q_0^2m\sqrt{\dfrac{k}{m}}=\pi q_0^2\sqrt{mk}}$$
変換後 $${\dfrac{Q'^2}{ \dfrac{mkq_0^2}{\lambda_1} }+\dfrac{P'^2}{ \dfrac{mkq_0^2}{\lambda_2} }=1}$$ (4-T")
$${S'=\pi\sqrt{\dfrac{mkq_0^2}{\lambda_1}}\sqrt{\dfrac{mkq_0^2}{\lambda_2}}=\pi q_0^2mk\sqrt{\dfrac{1}{\lambda_1\lambda_2}}}$$
$${=\pi q_0^2mk\sqrt{\dfrac{2×2}{(2mk+1+\sqrt{4m^2k^2+1})(2mk+1-\sqrt{4m^2k^2+1})}}}$$
$${=\pi q_0^2mk\sqrt{\dfrac{4}{(2mk+1)^2-(4m^2k^2+1)}}}$$
$${=\pi q_0^2mk\sqrt{\dfrac{4}{4m^2k^2+4mk+1-4m^2k^2-1}}}$$
$${=\pi q_0^2mk\sqrt{\dfrac{4}{4mk}}=\pi q_0^2\sqrt{mk}}$$
よって$${S=S'}$$
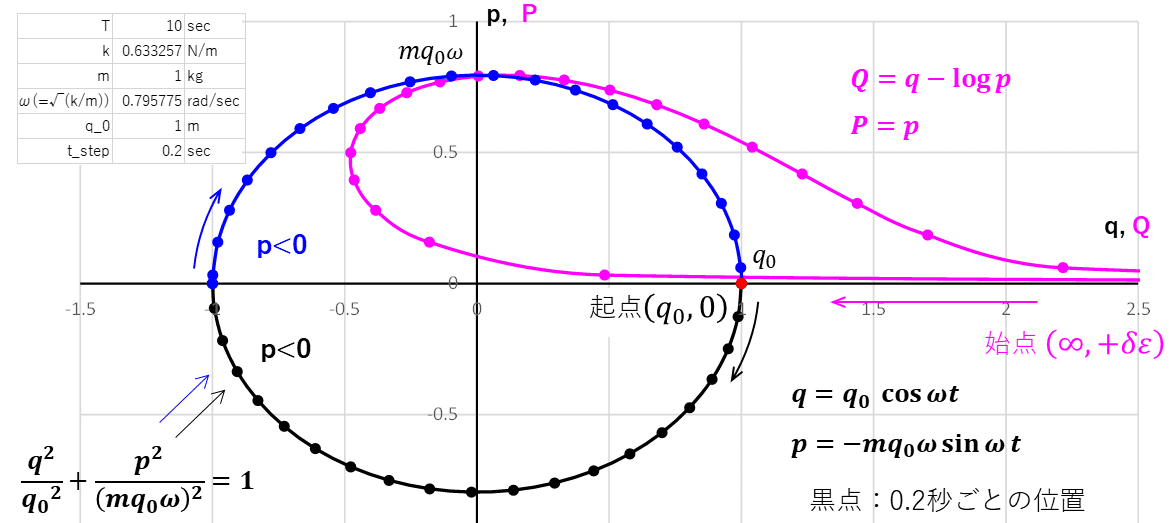
5 q=Q+logP, p=P
これも0からの変換を考える。
$${q=Q+\log P}$$ (5-q) $${p=P}$$ (5-p)
$${Q=q-\log P=q-\log p}$$ (5-Q) $${P=p}$$ (5-P)
(0-H)$${\mathscr{H}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}}$$より
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}}$$ (5-q') $${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=-kq}$$ (5-p')
(5-q)(5-p)を(0-H)に代入
$${\mathscr{\overline{H}}=\dfrac{p^2}{2m}+\dfrac{kq^2}{2}=\dfrac{P^2}{2m}+\dfrac{k(Q+\log P)^2}{2}}$$ (5-H)
Hamiltonの正準方程式を満たすかを確認する。
$${\dot{Q}}$$について
(5-Q)$${Q=q-\log P=q-\log p}$$より
$${\dot{Q}=\dot{q}-\dfrac{\dot{p}}{p}}$$ ←(5-q')$${\dot{q}=\dfrac{p}{m}}$$、(5-p')$${\dot{p}=-kq}$$を代入
$${=\dfrac{p}{m}+\dfrac{kq}{p}}$$ (5-Q'-1)
(5-H)$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{k(Q+\log P)^2}{2}}$$より
$${\dot{Q}=\dfrac{dQ}{dt}=\dfrac{\partial\mathscr{\overline{H}}}{\partial P}=\dfrac{P}{m}+k(Q+\log P)\dfrac{1}{P}}$$
←(5-p)$${p=P}$$、(5-q)$${q=Q+\log P}$$、(5-P)$${P=p}$$
$${=\dfrac{p}{m}+\dfrac{kq}{p}}$$ (5-Q'-2) よって(5-Q'-1)=(5-Q'-2)
$${\dot{P}}$$について
(5-P)$${P=p}$$より
$${\dot{P}=\dot{p}=-kq}$$ (5-P'-1) ←(5-p')$${\dot{p}=-kq}$$
(5-H)$${\mathscr{\overline{H}}=\dfrac{P^2}{2m}+\dfrac{k(Q+\log P)^2}{2}}$$より
$${\dot{P}=\dfrac{dP}{dt}=-\dfrac{\partial\mathscr{\overline{H}}}{\partial Q}=-k(Q+\log P)}$$ ←(5-q)$${q=Q+\log P}$$
$${=-kq}$$ (5-P'-2) よって(5-P'-1)=(5-P'-2)
というわけでHamiltonの正準方程式は成り立つ。
トラジェクトリーを考える。
$${Q=q-\log p}$$ (5-Q) $${P=p}$$ (5-P)
ちなみに $${q=q_0\cos\omega t}$$ (0-q) $${p=-mq_0\omega\sin\omega t}$$ (0-p)
$${Q}$$の中に$${\log p}$$が含まれている。
ということは、真数>0なので$${p>0}$$でなければならない。
(5-p)より$${p>0}$$になるのは
$${2n\pi+\pi<\omega t<2n\pi+2\pi}$$ ($${n}$$:正の整数)
つまり
$${\dfrac{(2n+1)\pi}{\omega}}$$$${ < t < \dfrac{2(n+1)\pi}{\omega}}$$ のときである。
0のトラジェクトリー(黒と青の楕円)は$${q_0, 0}$$を始点として時計回りだ
が、5のトラジェクトリーは黒の領域$${(p<0)}$$では存在せず、青の領域
$${(p>0)}$$に入ったところで、$${(\infty, \delta\epsilon)}$$からやってきて青の領域が終わると
$${(\infty, \delta\epsilon)}$$に消えていくことを周期的にくり返す。
どの資料にも単振動からの変換は載っているが、それ以外の記述はあまりない。正準変換をすることのメリットは周期運動以外ではないのか。
またトラジェクトリーは円と直線への場合しか見つけられなかった。円や楕円への変換では面積が保存されるが、閉じた面積が存在するのは周期運動だけである、多分。このことと関係するのか。
