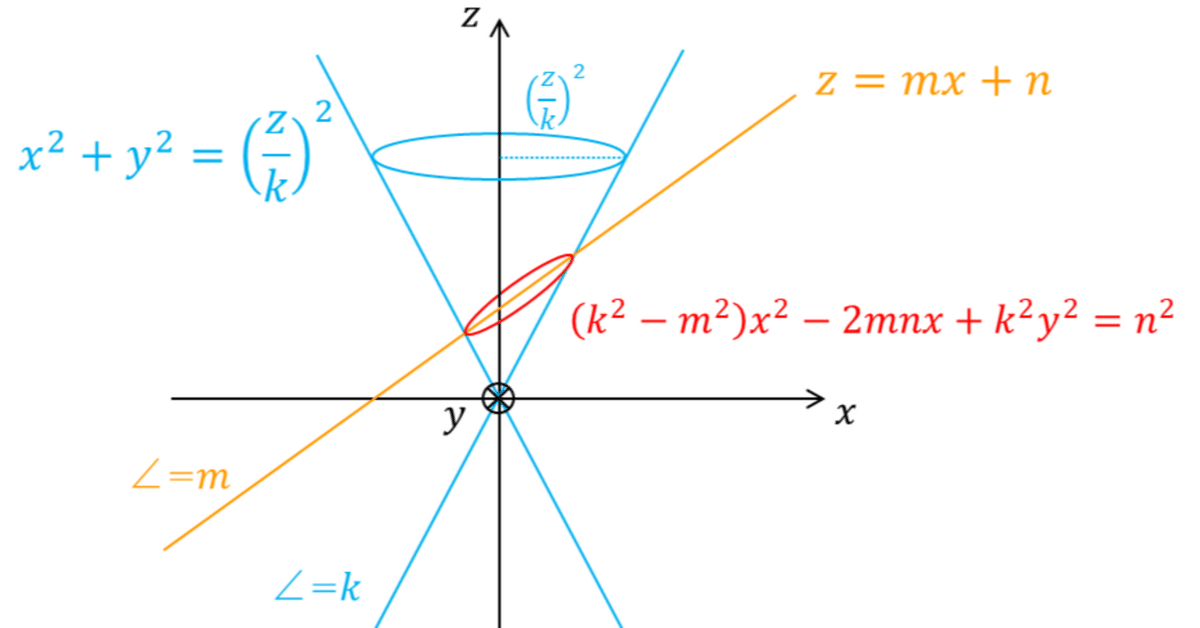
円錐曲線
円錐と円錐と交わる平面の交線を円錐を円錐曲線といい、交わり方によって交線は楕円、双曲線、放物線となる。
使おうと思ったらかなり錆びていた。思い出しついでにまとめた。
1 円錐の切り口
アポロニウスの見事な図形で攻める証明があるが、ここでは愚直に3次元座標で攻める。
頂点を原点とし$${z}$$軸の上下に傾き$${k}$$の側面が延びる円錐を$${x^2+y^2=\Big(\dfrac{z}{k}\Big)^2 (r>0)}$$、円錐と交わる傾き$${m}$$の平面を$${z=mx+n}$$とする。
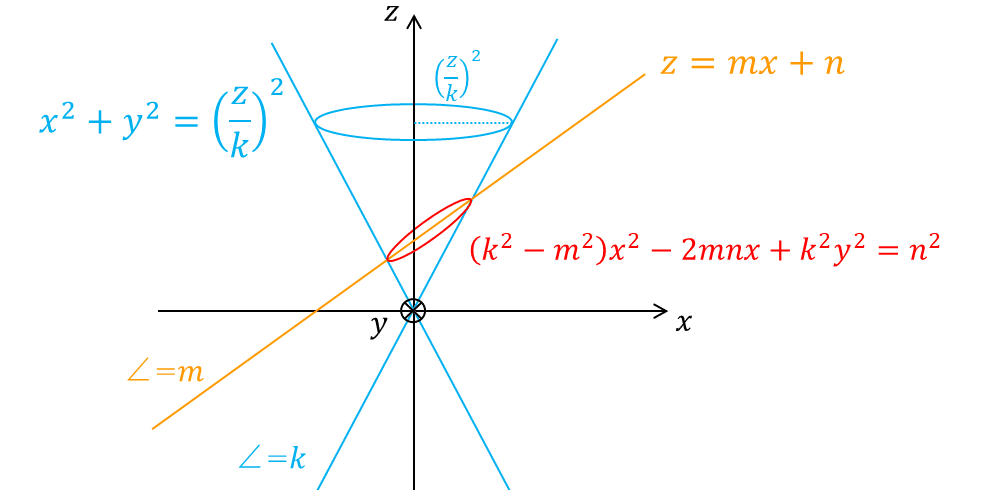
交線の方程式は
$${x^2+y^2=\Big(\dfrac{mx+n}{k}\Big)^2, k^2x^2+k^2y^2=m^2x^2+2mnx+n^2}$$
$${(k^2-m^2)x^2-2mnx+k^2y^2=n^2}$$ (1-1)
i) $${k^2-m^2=0}$$のとき
すなわち$${k=\pm m}$$、円錐面と平面の傾きが等しいとき
(1-1)は$${-2mnx+k^2y^2=n^2}$$となり $${y^2=\dfrac{2mn}{k^2}x+\dfrac{n^2}{k^2}}$$
交線は放物線である。(標準形 $${y^2=4px}$$)
ii) $${k^2-m^2\neq0}$$のとき
(1-1)を変形する
$${(k^2-m^2)\Big(x^2-\dfrac{2mn}{k^2-m^2}x\Big)+k^2y^2=n^2}$$
$${(k^2-m^2)\Big\{\Big(x-\dfrac{mn}{k^2-m^2}\Big)^2-\Big(\dfrac{mn}{k^2-m^2}\Big)^2\Big\}+k^2y^2=n^2}$$
$${(k^2-m^2)\Big(x-\dfrac{mn}{k^2-m^2}\Big)^2-\dfrac{m^2n^2}{k^2-m^2}+k^2y^2=n^2}$$
$${(k^2-m^2)\Big(x-\dfrac{mn}{k^2-m^2}\Big)^2+k^2y^2=\dfrac{m^2n^2}{k^2-m^2}+n^2}$$
$${=\dfrac{m^2n^2+k^2n^2-m^2n^2}{k^2-m^2}=\dfrac{k^2n^2}{k^2-m^2}}$$
$${\dfrac{\Big(x-\dfrac{mn}{k^2-m^2}\Big)^2}{\dfrac{k^2n^2}{(k^2-m^2)^2}}+\dfrac{y^2}{\dfrac{n^2}{k^2-m^2}}=1}$$
ii-1) $${k^2-m^2>0}$$のとき
すなわち$${|k|>|m|}$$、円錐面の傾きが平面の傾きより大きいとき
$${y^2}$$のの係数は正となり 交線は楕円である。
(標準形 $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$)
ii-2) $${k^2-m^2<0}$$のとき
すなわち$${|k|<|m|}$$、円錐面の傾きが平面の傾きより小さいとき
$${y^2}$$のの係数は負となり 交線は双曲線である。
(標準形 $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$)
以上をまとめる。
円錐面と平面が交わるとき、その交線は
円錐面の傾き>平面の傾き のとき 楕円
円錐面の傾き=平面の傾き のとき 放物線
円錐面の傾き<平面の傾き のとき 双曲線 である。
2 準線、焦点からの距離
2-1 放物線
定点(焦点$${\text{F}(p,0)}$$)と定直線(準線$${x=-p}$$)からの距離が等しい
点$${\text{P}(x, y)}$$の軌跡である。($${p\neq0}$$)
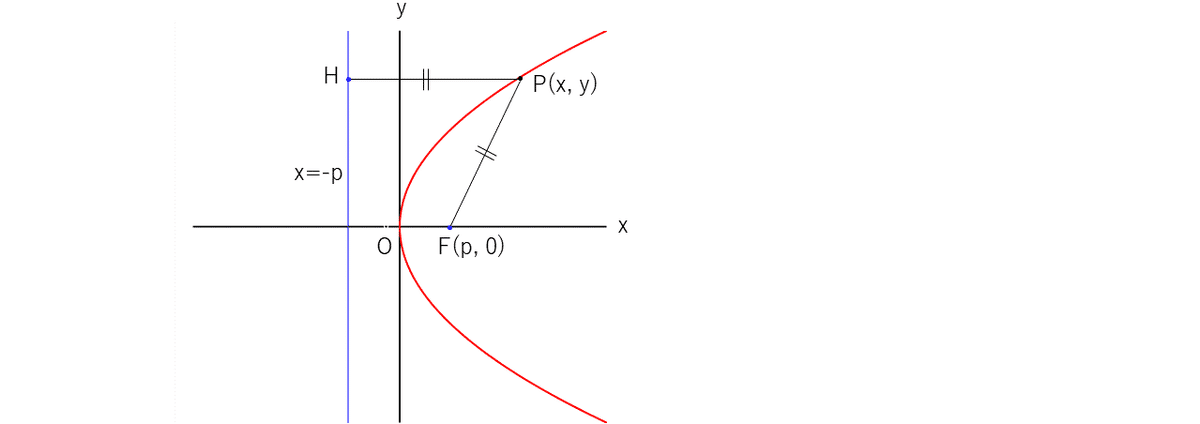
$${\overline{\text{PF}}=\overline{\text{PH}}}$$より $${\sqrt{(x-p)^2+y^2}=|x-(-p)|}$$
2乗して $${(x-p)^2+y^2=(x+p)^2}$$
$${x^2-2px+p^2+y^2=x^2+2px+p^2}$$
よって $${y^2=4px}$$ (2-1)(標準形)
または$${x}$$、$${y}$$を入れ替えて $${x^2=4py}$$ (2-2)(標準形2)
2-2 楕円
2定点(焦点$${\text{F}(c,0), \text{F'}(-c,0)}$$)からの距離の和($${2a}$$とする)が等しい
点$${\text{P}(x, y)}$$の軌跡である。($${c\neq0, a>c>0}$$)
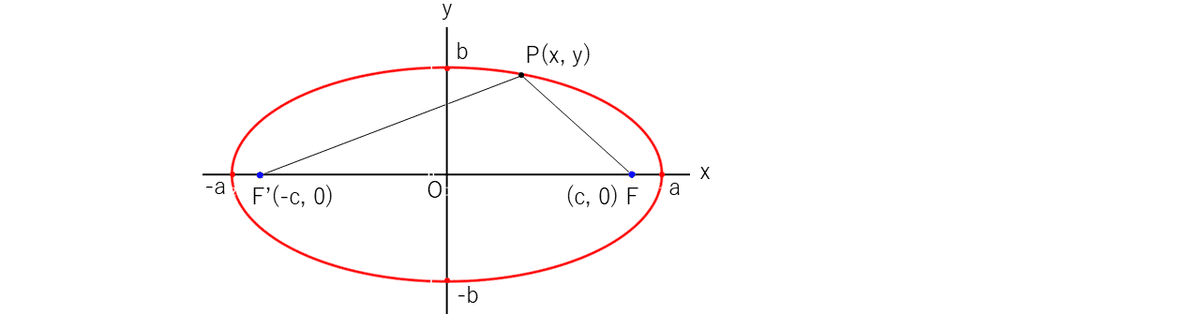
$${\overline{\text{PF}}+\overline{\text{PF'}}=2a}$$より $${\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a}$$
$${\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}}$$
2乗して
$${(x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2}$$
$${x^2-2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2}$$
$${-2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx}$$
$${4a\sqrt{(x+c)^2+y^2}=4a^2+4cx}$$
$${a\sqrt{(x+c)^2+y^2}=a^2+cx}$$
2乗して
$${a^2x^2+2a^2cx+a^2c^2+a^2y^2=a^4+2a^2cx+c^2x^2}$$
$${a^2x^2+a^2c^2+a^2y^2=a^4+c^2x^2}$$ $${(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)}$$
$${\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1}$$
$${a^2-c^2=b^2}$$とおくと $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$(2-3)(標準形)
2-3 双曲線
2定点(焦点$${\text{F}(c,0), \text{F'}(-c,0)}$$)からの距離の差($${2a}$$とする)が等しい
点$${\text{P}(x, y)}$$の軌跡である。($${c\neq0, a>c>0}$$)
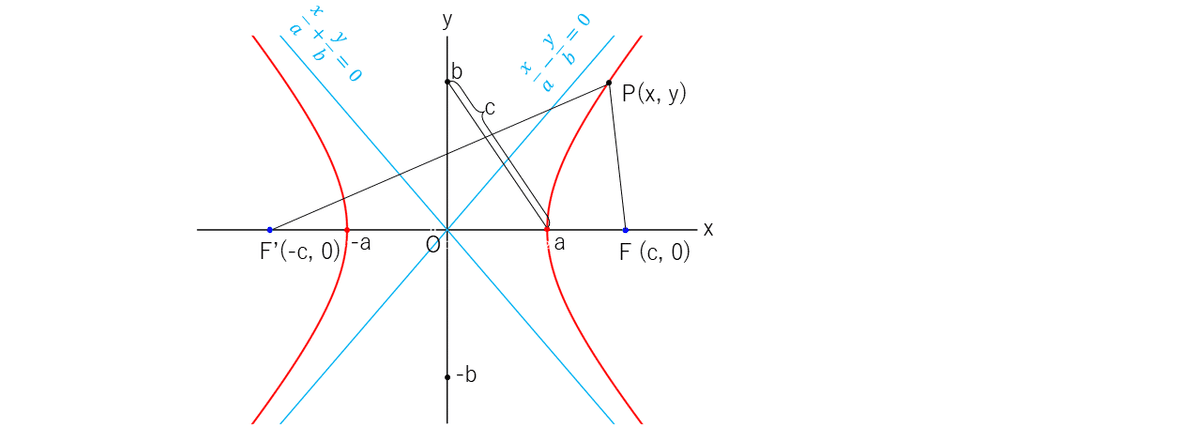
$${\overline{\text{PF}}-\overline{\text{PF'}}=\pm2a}$$より $${\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm2a}$$
$${\sqrt{(x-c)^2+y^2}=\pm2a+\sqrt{(x+c)^2+y^2}}$$
2乗して
$${(x-c)^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2}$$
$${x^2-2cx+c^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2}$$
$${\mp4a\sqrt{(x+c)^2+y^2}=4a^2+4cx}$$ $${\mp a\sqrt{(x+c)^2+y^2}=a^2+cx}$$
2乗して
$${a^2x^2+2a^2cx^2+a^2c^2+a^2y^2=a^4+2a^2cx+c^2x^2}$$
$${(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)}$$
$${\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1}$$ $${\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1}$$
$${c^2-a^2=b^2}$$とおくと $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$(2-4)(標準形)
これを$${y}$$について解くと $${\dfrac{y^2}{b^2}=\dfrac{x^2}{a^2}-1, y^2=\dfrac{b^2}{a^2}x^2\Big(1-\dfrac{a^2}{x^2}\Big)}$$
すなわち $${y=\pm\dfrac{b}{a}x\sqrt{1-\dfrac{a^2}{x^2}}}$$
$${|x|}$$が限りなく大きくなると$${y}$$は限りなく$${\pm\dfrac{b}{a}x}$$に近づく。
$${y=\dfrac{b}{a}x}$$と$${y=-\dfrac{b}{a}x}$$の2直線を漸近線という。
(または $${\Big(\dfrac{x}{a}-\dfrac{y}{b}\Big)\Big(\dfrac{x}{a}+\dfrac{y}{b}\Big)=0}$$)
漸近線は $${\dfrac{x}{a}\pm\dfrac{y}{b}=0}$$である。
以上をまとめる。 標準形
焦点F(p,0)と準線x=-pの距離が等しい点の軌跡
放物線 $${y^2=4px}$$
焦点F(c,0)、F'(-c,0)との距離の和が一定の点の軌跡
楕円 $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 (a^2-b^2=c^2)}$$
焦点F(c,0)、F'(-c,0) との距離の差が一定の点の軌跡
双曲線 $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 (a^2+b^2=c^2)}$$ 漸近線 $${y=\pm\dfrac{b}{a}x}$$
である。
3 離心率
定点$${F(p,0)}$$との距離と定直線$${l(x=-p)}$$との距離の比が一定の点Pの軌跡を考える。$${l}$$(準線という)にPから垂直に下した点をHとし、離心率$${\dfrac{FP}{PH}=e (e>0)}$$(3-1)を定義する。
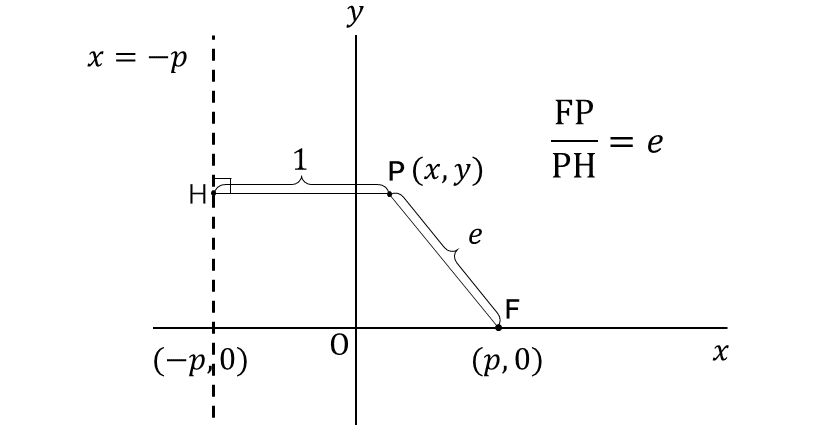
Pの座標を$${(x,y)}$$とすると
$${\overline{\text{FP}}=\sqrt{(x-p)^2+y^2}, \overline{\text{PH}}=\sqrt{(x+p)^2}}$$
(3-1)に代入する。
$${\dfrac{\sqrt{(x-p)^2+y^2}}{\sqrt{(x+p)^2}}=e, (x-p)^2+y^2=e^2(x+p)^2}$$
$${x^2-2px+p^2+y^2=e^2x^2+2e^2px+e^2p^2}$$
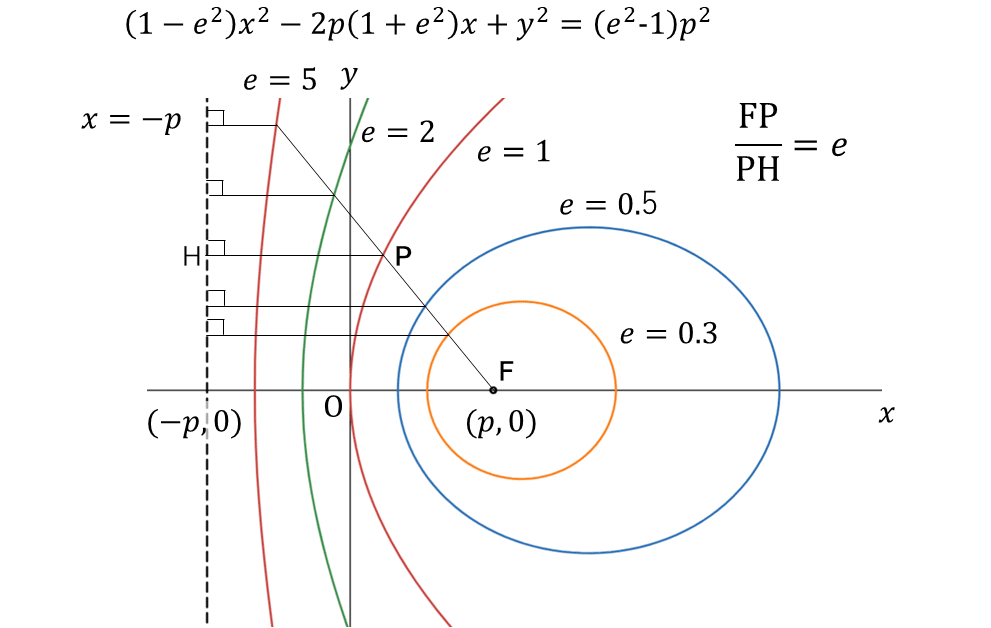
$${(1-e^2)x^2-2p(1+e^2)x+y^2=(e^2-1)p^2}$$ (3-2)
i) $${1-e^2=0}$$のとき すなわち$${e=1}$$のとき
(3-2)は$${-2p(1+1)x+y^2=0, y^2=4px}$$ 放物線である。
ii) $${1-e^2\neq0}$$のとき
(3-2)を変形する
$${(1-e^2)\Big\{x^2-\dfrac{2p(1+e^2)}{1-e^2}x\Big\}+y^2=(e^2-1)p^2}$$
$${(1-e^2)\Big[\Big\{x-\dfrac{p(1+e^2)}{1-e^2}\Big\}^2-\dfrac{p^2(1+e^2)^2}{(1-e^2)^2}\Big]+y^2=(e^2-1)p^2}$$
$${(1-e^2)\Big\{x-\dfrac{p(1+e^2)}{1-e^2}\Big\}^2-\dfrac{p^2(1+e^2)^2}{(1-e^2)}+y^2=(e^2-1)p^2}$$
$${(1-e^2)\Big\{x-\dfrac{(1+e^2)p}{1-e^2}\Big\}^2+y^2=\dfrac{p^2(1+e^2)^2}{(1-e^2)}+(e^2-1)p^2}$$
$${=\dfrac{p^2\{(1+e^2)^2-(1-e^2)^2\}}{(1-e^2)}=\dfrac{4e^2p^2}{(1-e^2)}}$$
$${\dfrac{\Big\{x-\dfrac{(1+e^2)p}{1-e^2}\Big\}^2}{\dfrac{4e^2p^2}{(1-e^2)^2}}+\dfrac{y^2}{ \dfrac{4e^2p^2}{1-e^2} }=1}$$
ii-1) $${e < 1}$$のとき
$${y^2}$$の項>0なので $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$ の形 よって楕円
ii-2) $${e > 1}$$のとき
$${y^2}$$の項<0なので $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$ の形 よって双曲線
以上をまとめる。
$${e=1}$$のとき 放物線
$${e < 1}$$のとき 楕円($${}$$)
$${e > 1}$$のとき 双曲線 である。
4 極座標による表示
焦点(直交座標で$${(p,0)}$$)のひとつを極座標$${(r.\theta)}$$の原点とする。
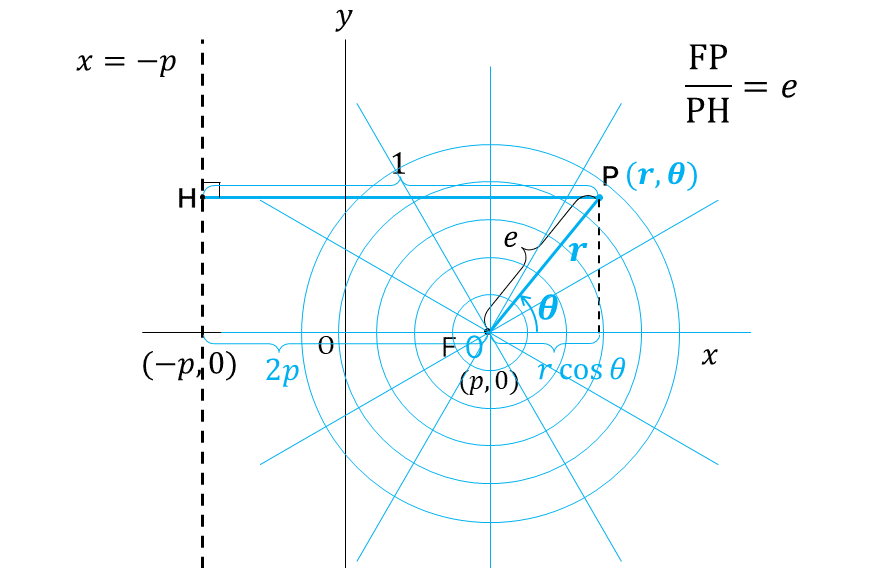
$${\overline{\text{FP}}=r, \overline{\text{PH}}=2p+r\cos\theta, \dfrac{\overline{\text{FP}}}{\overline{\text{PH}}}=\dfrac{r}{2p+r\cos\theta}=e}$$
$${r=e(2p+r\cos\theta)=2ep+er\cos\theta, (1-e\cos\theta)r=2ep}$$
$${r=\dfrac{2ep}{1-e\cos\theta}}$$ $${l=2ep}$$として
(焦点ー準線の距離に離心率をかけたもの。半直弦 or 半通径と呼ばれる)
$${r=\dfrac{l}{1-e\cos\theta}}$$ (4) $${e=1}$$のとき 放物線
$${e < 1}$$のとき 楕円
$${e > 1}$$のとき 双曲線
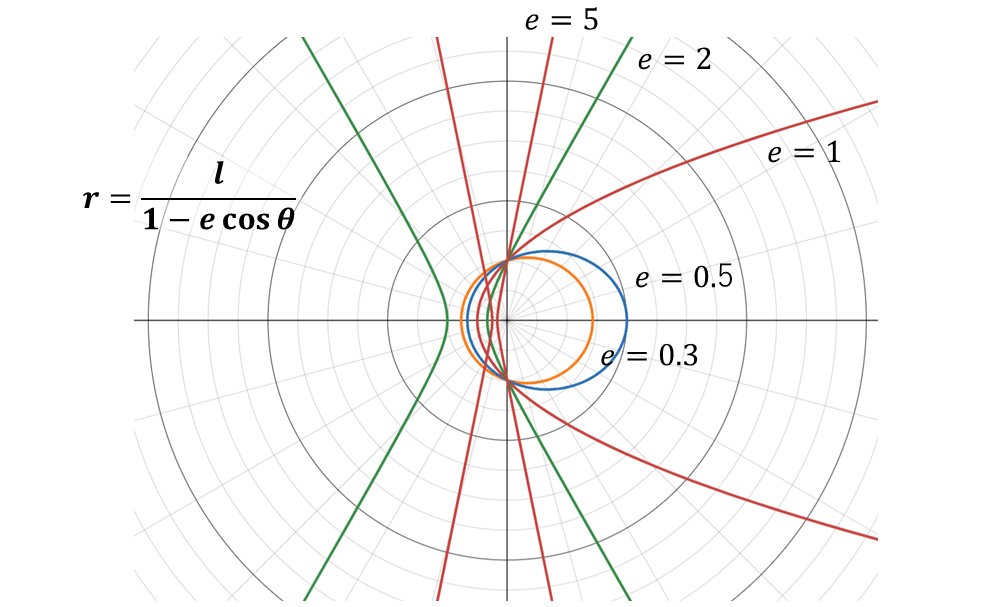
5 a,b ⇔ e,l
5-1 楕円の場合
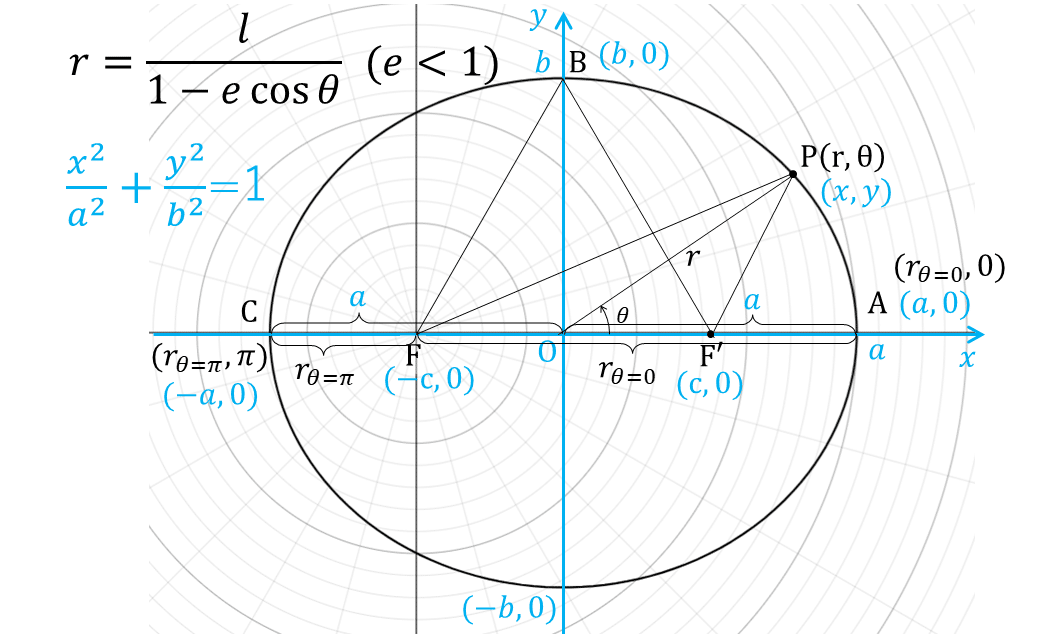
$${a=\dfrac{\overline{\text{AC}}}{2}=\dfrac{\overline{\text{FA}}+\overline{\text{FC}}}{2}=\dfrac{r_{\theta=0}+r_{\theta=\pi}}{2}=\dfrac{1}{2}\Big(\dfrac{l}{1-e\cos0}+\dfrac{l}{1-e\cos\pi}\Big)}$$
$${=\dfrac{1}{2}\Big(\dfrac{l}{1-e}+\dfrac{l}{1+e}\Big)=\dfrac{l(1+e+1-e))}{2(1-e^2)}=\dfrac{l}{1-e^2}}$$
$${b=\overline{\text{OB}}=\sqrt{\overline{\text{F'B}}^2-\overline{\text{OF'}}^2}=\sqrt{\overline{\text{F'B}}^2-\Big(\dfrac{\overline{\text{FA}}-\overline{\text{F'A}}}{2}\Big)^2}}$$
$${=\sqrt{\overline{\text{F'B}}^2-\Big(\dfrac{\overline{\text{FA}}-\overline{\text{FB}}}{2}\Big)^2}=\sqrt{\overline{\text{F'B}}^2-\Big(\dfrac{r_{\theta=0}-r_{\theta=\pi}}{2}\Big)^2}}$$
← $${\overline{\text{F'B}}=\dfrac{\overline{\text{FB}}+\overline{\text{F'B}}}{2}=\dfrac{\overline{\text{FA}}+\overline{\text{F'A}}}{2}}$$(楕円の定義)
$${=\dfrac{\overline{\text{FA}}+\overline{\text{FB}}}{2}}$$ ← $${\overline{\text{FA}}=\overline{\text{FB}}}$$
$${=\dfrac{r_{\theta=0}+r_{\theta=\phi}}{2}}$$
$${=\sqrt{\Big(\dfrac{r_{\theta=0}+r_{\theta=\phi}}{2}\Big)^2-\Big(\dfrac{r_{\theta=0}-r_{\theta=\pi}}{2}\Big)^2}=\sqrt{\dfrac{4 r_{\theta=0} r_{\theta=\pi}}{4}}}$$
$${=\sqrt{r_{\theta=0} r_{\theta=\pi}}=\sqrt{\dfrac{l}{1-e}\dfrac{l}{1+e}}=\dfrac{l}{\sqrt{1-e^2}}=\sqrt{\dfrac{l}{1-e^2}\times l}(=\sqrt{al})}$$
$${c=\sqrt{a^2-b^2}=\sqrt{\Big(\dfrac{l}{1-e^2}\Big)^2-\Big(\dfrac{l}{\sqrt{1-e^2}}\Big)^2}=\sqrt{\dfrac{l^2(1-1+e^2)}{(1-e^2)^2}}}$$
$${=\dfrac{el}{1-e^2}(=ae)}$$
$${e=\dfrac{c}{a}=\dfrac{\sqrt{a^2-b^2}}{a}}$$
まとめる。
$${a=\dfrac{l}{1-e^2}}$$、 $${b=\dfrac{l}{\sqrt{1-e^2}} (=\sqrt{al})}$$、 $${c=\dfrac{el}{1-e^2} (=ae)}$$
$${e=\dfrac{\sqrt{a^2-b^2}}{a}}$$
5-2 双曲線の場合
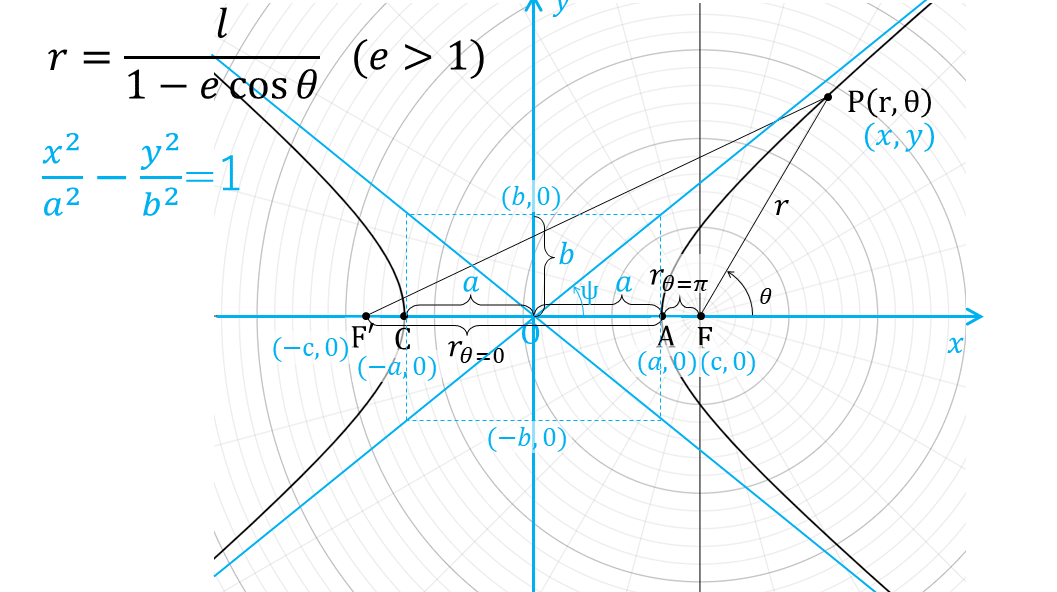
$${a=\dfrac{\overline{\text{AC}}}{2}=\dfrac{\overline{\text{AF'}}-\overline{\text{F'C}}}{2}=\dfrac{\overline{\text{AF'}}-\overline{\text{FA}}}{2}}$$
$${=\dfrac{|r_{\theta=0}|-r_{\theta=\pi}}{2}=\dfrac{1}{2}\Big(\Big|\dfrac{l}{1-e\cos0}\Big|-\dfrac{l}{1-e\cos\pi}\Big)}$$
$${=\dfrac{1}{2}\Big(\Big|\dfrac{l}{1-e}\Big|-\dfrac{l}{1+e}\Big)}$$ ← $${e>1}$$なので$${\dfrac{l}{1-e}<0}$$
$${=\dfrac{1}{2}\Big(-\dfrac{l}{1-e}-\dfrac{l}{1+e}\Big)=\dfrac{-l(1+e+1-e)}{2(1-e^2)}=\dfrac{l}{e^2-1}}$$
$${c=\overline{\text{OF}}=\overline{\text{OA}}+\overline{\text{AF}}=a+r_{\theta=\pi}=\dfrac{l}{e^2-1}+\dfrac{l}{1+e}=\dfrac{l(1+e-1)}{e^2-1}}$$
$${=\dfrac{el}{e^2-1} (=ae)}$$
$${b=\sqrt{c^2-a^2}=\sqrt{\Big(\dfrac{el}{e^2-1}\Big)^2-\Big(\dfrac{l}{e^2-1}\Big)^2}=\dfrac{l\sqrt{e^2-1}}{e^2-1}}$$
$${=\dfrac{l}{\sqrt{e^2-1}} ( =a\sqrt{e^2-1})}$$
上式より
$${b^2=a^2(e^2-1), e^2=\dfrac{b^2}{a^2}+1=\dfrac{a^2+b^2}{a^2}, e=\dfrac{\sqrt{a^2+b^2}}{a}}$$
まとめる。
$${a=\dfrac{l}{e^2-1}}$$、 $${b=\dfrac{l}{\sqrt{e^2-1}} ( =a\sqrt{e^2-1})}$$、 $${c=\dfrac{el}{e^2-1} (=ae)}$$
$${e=\dfrac{\sqrt{a^2+b^2}}{a}}$$
また漸近線の傾き
$${\tan\psi=\pm\dfrac{b}{a}, \psi=\pm\tan^{-1}\dfrac{b}{a}}$$
6 媒介変数による表示
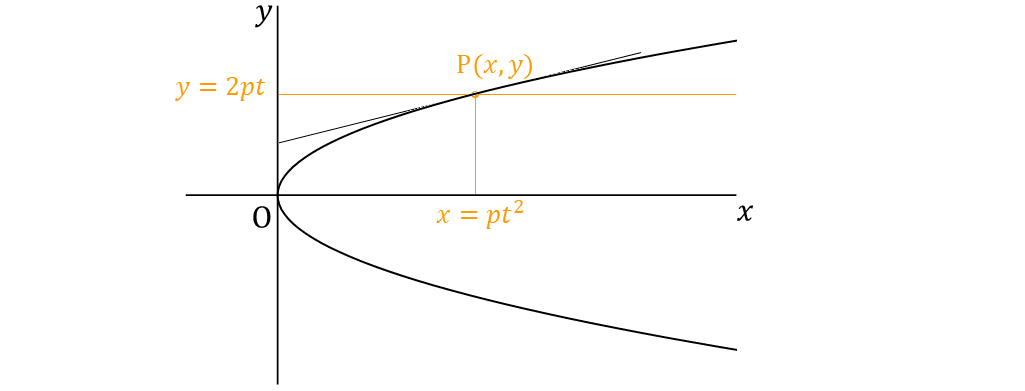
放物線 $${y=4px}$$ ← $${x=pt^2, y=2pt}$$ (5-1)
楕円 $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$ ← $${x=a\cos\theta, y=b\sin\theta}$$ (5-2)
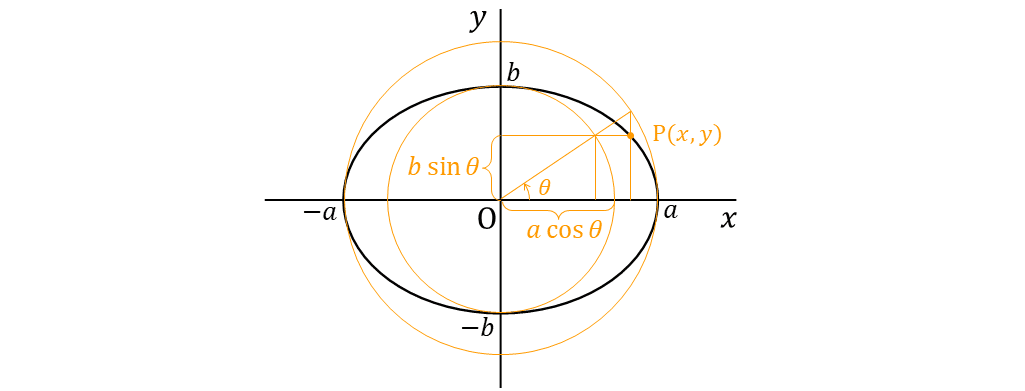
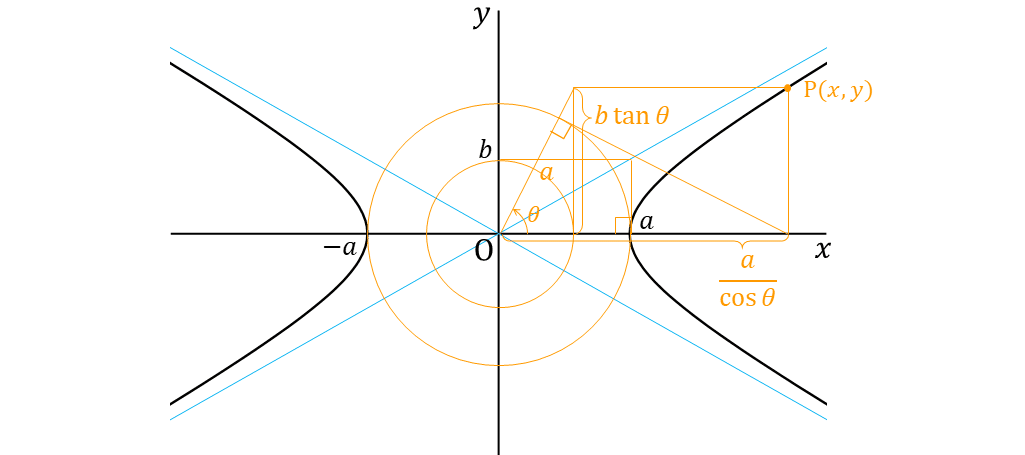
双曲線 $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$ ← $${x=\dfrac{a}{\cos\theta}, y=b\tan\theta}$$ (5-3)
放物線 $${y=4px}$$ ← $${x=pt^2, y=2pt}$$ (5-1)
楕円 $${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$ ← $${x=a\cos\theta, y=b\sin\theta}$$ (5-2)
双曲線 $${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$ ← $${x=\dfrac{a}{\cos\theta}, y=b\tan\theta}$$ (5-3)
この他にも
楕円 $${x=\dfrac{a(1-t^2)}{1+t^2}, y=\dfrac{2bt}{1+t^2}}$$ (5-4)
双曲線 $${x=\dfrac{a(1+t^2)}{1-t^2}, y=\dfrac{2bt}{1-t^2}}$$ (5-5)
$${\sin\theta=2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}=2\dfrac{\sin(\theta/2)}{\cos(\theta/2)}\cos^2\dfrac{\theta}{2}}$$
$${=\footnotesize{2\dfrac{\sin\dfrac{\theta}{2}}{\cos\dfrac{\theta}{2}}\dfrac{1}{\dfrac{\cos^2(\theta/2)+\sin^2(\theta/2)}{\cos^2(\theta/2)}}=2\tan\dfrac{\theta}{2}\dfrac{1}{ 1+\tan^2\dfrac{\theta}{2} }}}$$ ← $${\tan\dfrac{\theta}{2}=t}$$
$${=\dfrac{2t}{1+t^2}}$$
$${\cos\theta=\cos^2\dfrac{\theta}{2}-\sin^2\dfrac{\theta}{2}=2\cos^2\dfrac{\theta}{2}-1=\footnotesize{\dfrac{2}{\dfrac{\cos^2(\theta/2)+\sin^2(\theta/2)}{\cos^2(\theta/2)}}-1}}$$
$${=\dfrac{2}{1+\tan^2(\theta/2)}-1}$$ ← $${\tan\dfrac{\theta}{2}=t}$$
$${=\dfrac{2}{1+t^2}-1=\dfrac{2-1-t^2}{1+t^2}=\dfrac{1-t^2}{1+t^2}}$$
$${\tan\theta=\dfrac{\sin\theta}{\cos\theta}=\dfrac{2t/(1+t^2)}{(1-t^2)/(1+t^2)}=\dfrac{2t}{1-t^2}}$$
これらを(5-2)(5-3)に代入すると(5-4)(5-5)が得られる。
この他にも双曲線関数を用いたものなどがあるが、こんなもんにしとく。
→ 力学、物理数学の目次へ
