拡張版アンビグラムの冒険
「アンビグラム Advent Calendar 2023」の19日目を担当します、ぺんぺん草と申します。よろしくお願いします。
書く時間がとれなくて一日遅刻しましたごめんなさい…。
18日目の担当はえんぷてぃさんでした。素敵な作品の振り返り記事です。ぜひぜひ。
1 はじめに
アンビグラムには内包型と呼ばれるタイプがあります。
こんなの。

内包型は、本来は厳密なアンビグラムの定義を満たさないのですが、伝統的にアンビグラムとされてきたため、例外的にアンビグラムということになっているそうです。かなり肩身の狭い存在ですね。
この記事では、アンビグラムの定義を内包型のレベルにまで拡張して、あれこれ空想してみたいと思います。
2 拡張定義
まずそもそものアンビグラムの定義ですが、Discordの「アンビグラム情報局」>「アンビグラム基本情報」にいがときしんさんによる定義が紹介されていますので、そちらでご確認ください(勧誘)。
アンビグラムの基準として、文字図形同士が「同じ形をしている」という同形性がひとつポイントになってくるかと思います。内包型は同形性を満たさないので、いがときしんさんの定義では「その他」として例外的な形でアンビグラムに取り込まれています。
ここでは内包型も含むようにアンビグラムの定義を拡張したいので、同形性をもう一歩進めて、次のように拡張定義してみます。
拡張定義:「合同変換を施したときに、文字図形同士が同じ形を共有する」
※合同変換=回転・鏡映・並進(平行移動)とそれらの組み合わせ。
もしフラクタル型も取り込むのであれば、縮小・拡大を追加して相似変換に変更してください。
3 交差分類法
3-1 基本形
拡張定義に沿って拡張版アンビグラムを考えていきます。
まずは2つの文字図形A,Bが「同じ形を共有する」方法に着目してみましょう。円の交わりで表現すると、次のような4つの基本形が考えられます。
①「非交差」

②「交差」
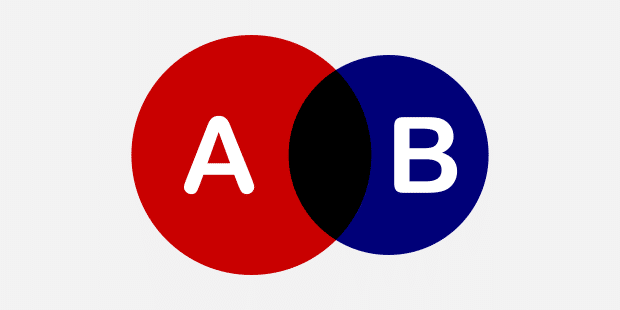
③「内包」

④「一致」

ちなみに「非交差」以外の基本形は包含関係にあります。つまり、「交差」の中の特殊な形が「内包」であり、更にその「内包」の中の特殊な形が「一致」となります。

3-2 交差分類
上記の基本形をもとにすると、次のような分類表を作成することができます。

ここでいうnは、文字図形の個数です。上図の場合、文字図形はAとBの2個だけなので、n=2となります。
「一致型」は普段よく見る通常のアンビグラムのことですね。
「内包型」も普段よく見る内包型のことです。
「交差型」は例えば次のような型のことです。

「カロリー」と「OFF」が同じ形(紫色)を部分的に共有している
文字図形数がn=3になると場合の数が跳ね上がり複雑になりますが、それでも下図のようにやはり3つの型に分類することができます。

n=3までであれば、円の交わりによる表現はすっきりしていて視覚的にも分かりやすいのですが、nが大きくなると複雑になり視覚化も困難になってきます。そこで、次のような対応表で文字図形同士の関係を表現してみます。

更に考えを進めると、対応表は多分そのまま行列やベクトルに転化できるので、それをもとになんやかんややればいろいろと分析できそうな気がします。よくわからないですけど。
ちなみに一般のnに対して、大雑把に数えると組み合わせのパターンは多分5^(nC2)通りあります(ただし、すべての関係が「非交差」のようなパターンもいくつか含むので注意)。なので、nが大きくなると場合の数は指数関数的に増加していきます。
※文系なのでこの辺はあまり自信がないです…。もし数学の得意な方がいらっしゃったら、ぜひちゃんとした一般項を教えてください。
4 図地反転型の解釈
交差分類を考えるときに、図地反転型の解釈が問題になってきます。
例えば下の『コーヒー』のようなタイプは、180°回転すると図と地が同じ形になるので、恐らく「一致型」として解釈できると思うのですが…

では次の『蛍雪』のようなタイプは何型になるのでしょうか…?

「蛍」と「雪」は、同じ形であるどころか、そもそも同じ形を共有すらしていません。そうすると、「一致型」「内包型」「交差型」のどれにもあてはまらないように思われます。
どう解釈したらよいのでしょうか。
4-1 仮説①非交差性仮説
1つ目の解釈。
3-1で説明した交差分類の基本形に、「非交差」というものがありました。

拡張定義では「同じ形を共有する」が大前提だったので、交差分類表では「非交差型」というのは考えていなかったのですが、『蛍雪』タイプは「非交差型」にあたるのではないでしょうか。

もしこの仮説が正しい場合、図地反転型というのは同形性を必要としないかなり特異なアンビグラムということになります。
4-2 仮説②総体性仮説
2つ目の解釈。
図地反転を、図と地でそれぞれ分離してとらえるのではなく、図地が一体となった「総体」としてとらえてみます。

「総体」の状態では図地が未分化ですが、認識を切り替えて図と地それぞれに着目したときに、「蛍」と「雪」それぞれに分化します。
(認識の切り替えについてはオルドビス紀さんのアドカレがとても参考になります)
そして「総体」の状態で比較したとき、『蛍雪』の「蛍」と「雪」は180°回転して同じ形になるので、図地反転型は「一致型」となります。
この総体性仮説にはメリットがいくつかあります。
・非交差性仮説と異なり、図地反転型を例外扱いしないこと
・例えば普通の90°回転型などに適用しても特に害がないこと
・kawahar box(局所的な図地反転)の解釈に有効であること などなど
ただ、図地反転型の拡張版(Dissection Ambigram?)について「総体」を考えたとき、各部分に余分な対応が増えてしまうので少し微妙な気もします。
5 拡張定義の死角
ところで今まで拡張定義として当たり前のように「同じ形を共有する」という表現を使っていましたが、その基準って何でしょう?
例えば次のような場合は、同じ形を共有していると言えるでしょうか?


確かに同じ形を共有しているのですが、アンビ性は一切感じられません。
ではどの程度以上の共有であればアンビ性が生じるのでしょうか?
恐らくこの問題は、「砂山のパラドックス」や「ハゲ頭のパラドックス」と同じように、明確な基準を設定できない事柄だと思います。
このことは内包型・交差型が根源的に抱える大きな欠点になります。
6 おまけ:縮小版内包型
この記事ではアンビグラムの定義を内包型レベルまで拡張するということを考えてきましたが、逆に内包型をアンビグラムの定義に組み込む考え方を紹介します。
アンビグラムの創始者の一人であるスコット・キムは、著作『Inversion』でアンビグラムを次のように分類しています。

内包型は「知覚的機構」(認識の切り替え)に分類されていますね。
スコット・キムの説明によると、内包型は、色を使うことで「全体 / 部分」という2種類の解釈を与えることができるそうです。

これは振動型や図地反転型にかなり近い考え方だと思います。
考えてみると、振動型作品に余分な線や点がついていることはよくあるので、内包型を余分な部分のついた振動型と解釈することはそれ程無茶な話ではないと思います。あるいは総体性仮説を導入すれば、図地反転と同様、内包型にも同形性を認められるような気がします。
ひとつだけ、次のように分解して展示すると「全体 / 部分」の認識の切り替えが起きないことには注意してください。

7 おわりに
これからそう遠くない未来に、日本語アンビグラムを自動生成するAIが出現するでしょう。そして人間の手では作成困難なアンビグラム――例えば文字図形数n=666のような悪魔的対応――が一瞬で生成される時代が到来します。ネットにあふれかえるAI産の複雑怪奇なアンビグラム群。なす術なく崩れ落ちる我々人類。そんなアンビグラム的末法の世にこそ、分析法として交差分類法は活躍するのではないかとひそかに妄想していたりします。
最後に。勢いで書いたので説明不足や思慮不足、誤りなど多々あるかと思います。ぜひこの記事をたたき台にして、X(故Twitter)やDiscordのアンビグラム情報局などで議論していただければ嬉しいです。
長文にもかかわらず最後までお付き合いいただきありがとうございました。
明日20日目は同じ草仲間の(と勝手にお慕いしている)晴草さんが担当です。お楽しみに!
