【ごまかんぱちの挑戦】エクセルでAutoCADの自動作図（その12）

こんにちは。ごまかんぱちです。🐟

AutoCADの自動作図を目指して奮闘しています。
第12回を迎えました。今回の題材は らせん階段です。

12-1. らせん階段

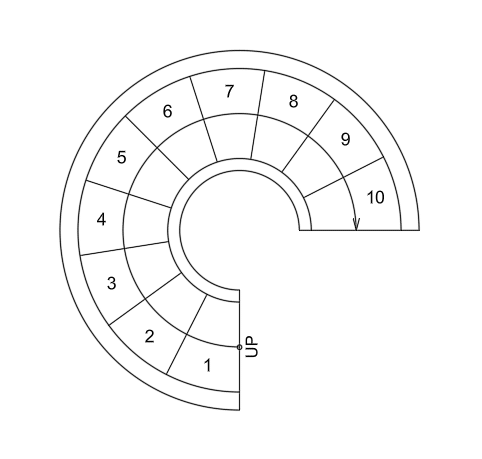
こんな感じの らせん階段を描いてみます。ありがちですね。

エクセルは こうなります。

通路の幅（セルI7）には、緑四角の式を入力することで、自動で計算します。
そのほかの 黄色のセルは すべて手動で入力しましょう。

青い文字は I列の数字から持って来ています。
なくてもいいですが、あると視覚的にわかりやすくなりますね。😊

まずは 円弧を1つ描いてみましょう。
セルI4の値を使います。

    Print #1, "arc c " & 0 & "," & 0 & " " & Range("I4") / 2 & "," & 0 & " " & 0 & "," & -Range("I4") / 2       '外側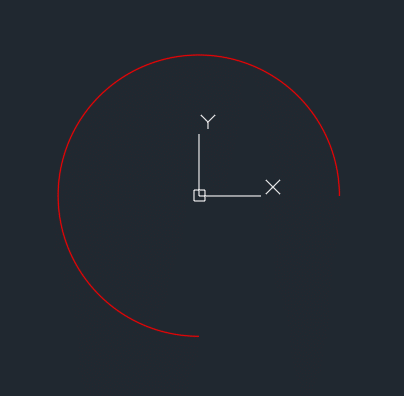

できました。😊
円弧の解説は （その10）をご覧ください。

続いて 内側の円弧。
それと 線を2本描きます。

'◆外形
Print #1, "clayer Layer1"       '画層の指定

Print #1, "arc c " & 0 & "," & 0 & " " & Range("I4") / 2 & "," & 0 & " " & 0 & "," & -Range("I4") / 2       '外側
Print #1, "arc c " & 0 & "," & 0 & " " & Range("I3") / 2 & "," & 0 & " " & 0 & "," & -Range("I3") / 2       '内側

Print #1, "line " & Range("I3") / 2 & "," & 0 & " " & Range("I4") / 2 & "," & 0 & " "       '端部（終点）
Print #1, "line " & 0 & "," & -Range("I3") / 2 & " " & 0 & "," & -Range("I4") / 2 & " "     '端部（始点）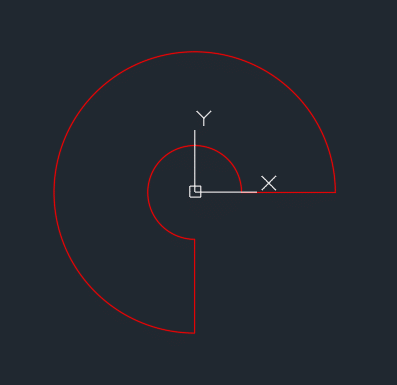

外形が完成しました。😊

続いて 手すりです。

Print #1, "arc c " & 0 & "," & 0 & " " & Range("I4") / 2 - Range("I6") & "," & 0 & " " & 0 & "," & -Range("I4") / 2 - Range("I6")    '外側
Print #1, "arc c " & 0 & "," & 0 & " " & Range("I3") / 2 + Range("I5") & "," & 0 & " " & 0 & "," & -Range("I3") / 2 + Range("I5")    '内側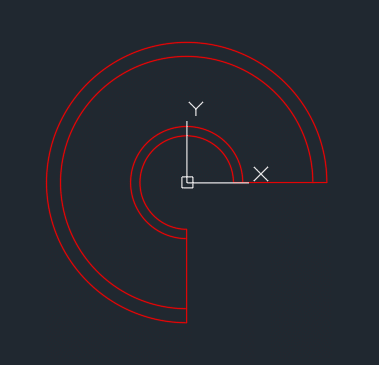

できました。順調です。😊

続いて 階段です。
まずは 1段目　　・・・その前に 練習です。

Angle1 = 270 * 4 * Atn(1) / 180                     '270°をラジアンに変換
Angle2 = 270 * 4 * Atn(1) / 180 / Range("I9")       '階段1段分の角度「270°÷セルI9の値」をラジアンに変換

'練習
Print #1, "clayer Layer2"       '画層の指定
Print #1, "line " & 0 & "," & 0 & " " & 1000 * Cos(Angle1 - Angle2) & "," & 1000 * Sin(Angle1 - Angle2) & " "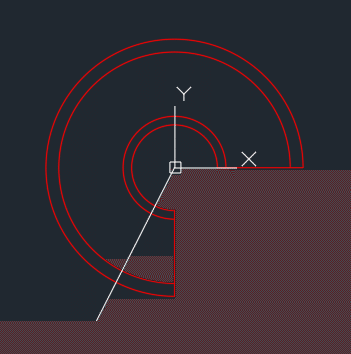

できました。
階段の1段目が来る角度に 仮の線を引きました。
画層を変えて 目立つようにしています。

解説です。
まずは 角度のお話。

よくわからないので わかりやすく書くと、1行目は 次のような意味です。
　Angle1＝270°×π/180°

この式の右辺では、角度270°に π/180°を掛けています。
VBAの世界では、角度を扱うときの単位はラジアンです。
なので、角度270°をラジアンに変換している ということです。

πについての 詳しい解説は （その10）にあります。

2行目も同様です。
　Angle2＝270° ÷（セルI9の値）×π/180°

セルI9の値は、分割数（階段の段数）なので、階段1段あたりの角度をラジアンに変換したものです。

続いて 最後の行について。

座標1から座標2に線を引く ということです。
座標2について もう少し詳しく説明します。

Angle1は270°、Angle2はθのことです。（ラジアン表記）
つまり、最後の行の Angle1-Angle2は、
3時の方向を0°としたときの 階段1段目の位置までの角度を表しています。

X軸方向と Y軸方向に分解して
　Cos(Angle1-Angle2)
　Sin(Angle1-Angle2)
となるわけです。

それぞれに 長さ1000を掛けると 座標2は上記の式になります。
（練習なので 長さは何でもいいです。適当に1000にしました。）

ここまで 練習です。
長かったですね。😥

では 本番です。

Print #1, "line " & (Range("I3") / 2 + Range("I5")) * Cos(Angle1 - Angle2) & "," & (Range("I3") / 2 + Range("I5")) * Sin(Angle1 - Angle2) & " " & (Range("I4") / 2 - Range("I6")) * Cos(Angle1 - Angle2) & "," & (Range("I4") / 2 - Range("I6")) * Sin(Angle1 - Angle2) & " "

長いですが、大まかには 練習と同じなので 理解しやすいはずです。

結果はこう。

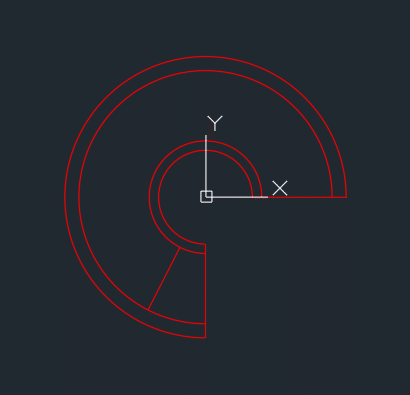
思い通りの線が描けました。😊
あとは この線を繰り返すだけです。

For i = 1 To Range("I9") - 1
    Print #1, "line " & (Range("I3") / 2 + Range("I5")) * Cos(Angle1 - Angle2 * i) & "," & (Range("I3") / 2 + Range("I5")) * Sin(Angle1 - Angle2 * i) & " " & (Range("I4") / 2 - Range("I6")) * Cos(Angle1 - Angle2 * i) & "," & (Range("I4") / 2 - Range("I6")) * Sin(Angle1 - Angle2 * i) & " "
Next

Angle2 を Angle2 * i に変えるだけです。意外とカンタンでした。😊
1段目をシッカリ作ることが大切ですね。😊😊

結果はこうなりました。

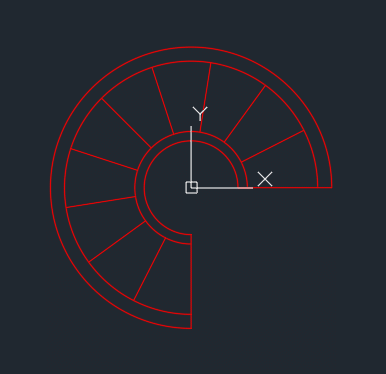
完璧です！
思い通りの図が 描けました！！😊

さあ あとはウイニングランです。
ちょっとした機能を追加していきましょう。

・UPの矢印を描く
・段数の数字を表記
・階段の範囲の角度を指定（現状の270°を可変に）

ぜひ 続きも読んでください。

12-2. アドバンス

さあ、どんどん階段を上りましょう。

・UPの矢印を描く

通路の真ん中に 円弧を描き、上り方向を示す矢印にします。