プログラミング初心者が株価予測してみた
目次
初めに
概要
実行環境
株価データの取得
株価予測の実践
終わりに
1.初めに
仕事でもデータの分析を行いたかったのと、株式投資に興味を持っていたので、データ分析の講座を受講しました。
2.概要
・Yahoo Financeから株価を取得
・SARIMAモデルを用いた時系列分析を行い、株価予測をします。
今回はTKCの株価データのうち終値のデータを用いて予測を行いました。
3.実行環境
・Python 3.9.12
・Jupyter Lab 3.3.2
・Windows-10-10.0.19045-SP0
実行環境は下記コードで確認しました。
!python -V
!jupyter-lab --version
import platform
platform.platform()4.株価データの取得
1.使用するライブラリをインポート
!pip install yfinance
#Yahoo Financeがインストールされていなかったため、インストールを行いました
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import itertools
import statsmodels.api as sm2.株価データの取得
Yahoo FinanceからTKC(銘柄コード9746)の2018年1月~2024年11月の株価データを取得し中身を確認します。
#ティッカーにTKC("9746.T")を指定。
#変数dfに株価データを代入。start,endで期間を指定。
ticker = "9746.T"
df = yf.download(ticker, start="2018-01-01", end="2024-11-30", interval="1d")
df
次に欠損値の確認を行います。
#欠損値の確認
df.isnull().sum()
欠損値がないことを確認できましたので、このデータを使用します。
次に、終値(Close)を月平均にリサンプルし、グラフで可視化します。
#終値の月平均にデータを変更する
df = df.resample(rule = "M").mean()
#グラフにして可視化
plt.plot(df["Close"])
plt.show()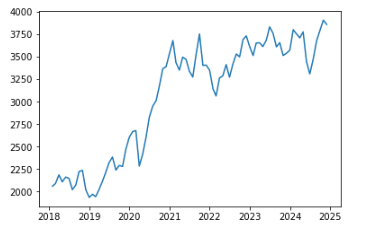
5.株価予測の実践
1.自己相関関数・偏自己相関
自己相関係数とは過去の値とどれだけ似ているかを表した値です。
偏自己相関とはある時点のデータが前のデータと相関がある場合にその影響を取り除いて相関を求めたものです。
自己相関関数と偏自己相関を可視化していきます。
#自己相関・偏自己相関の可視化
fig=plt.figure(figsize=(9, 7)) #matplotlibのグラフのサイズを指定
#自己相関係数のグラフを出力
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df["Close"], lags=30, ax=ax1)
#偏自己相関係数のグラフを出力
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df["Close"], lags=30, ax=ax2)
plt.show()

コレログラムから、周期性はないと言えます。
2.データパターンの確認
時系列分析において重要な概念が「定常性」です。定常性とは、時間に依らず時系列データの確率分布が変化しないという確率過程の性質を表し、そのような確率過程を定常過程と呼びます。
言い換えると、時間の経過によらず一定の値を軸に同程度の幅で振れて変化すると言えます。
時系列データにおいて、定常性のないデータを分析した結果全く意味のない相関(Aが上がればBも上がる、もしくは下がるという関係)を検出してしまう可能性があります。
時系列データとは時間の経過に沿って変化するデータなので、「時間の経過」という共通項目が無意味な関係を生んでしまいます。このような無意味な相関の事を疑似相関といいます。
このような時系列データの疑似相関を検出しないために、定常性のない時系列は定常性のある時系列にしてから分析を進める必要があります。
時系列データを変換する方法の一つに、季節調整があります。
StatsModelsのtsa.sesonal_decompose()を使用することで、トレンド・季節変動・残差(=原系列-トレンド-季節変動)に分けることが可能です。残差は定常性のある時系列データになります。
sm.tsa.seasonal_decompose(df["Close"], period=12).plot()
plt.show()
1番上が原系列、2番目がトレンド、3番目が季節性、4番目が残差です。
グラフより、トレンドと季節性があることが分かります。
3.株価予測の実践
①モデル・パラメータの決定
取得した株価データを整理しパターンの確認をしたところ、トレンド・季節性があることが分かりました。
よって、SARIMAモデルを使って分析を行いたいと思います。
pythonにはSARIMAモデルのパラメータ(p,d,q) (sp,sd,sq,s)を自動で最も適切にしてくれる機能はありません。
そのため、情報量基準(今回はBIC(ベイズ情報量基準))によってどの値が最も適切か調べるプログラムを書きます。
BICの場合はこの値が低ければ低いほどパラメータの値は適切であると理解してください。
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return parameters[np.argmin(BICs)]
selectparameter(df["Close"],12)

②モデルの構築
最適なパラメータ(p,d,q),(sp,sd,sq,s)が分かったので、モデルを構築していきます。
#モデルの構築
SARIMA_MSFT = sm.tsa.statespace.SARIMAX(df["Close"],order=(0, 1, 0),seasonal_order=(0, 1, 1, 12)).fit()
print(SARIMA_MSFT.bic)
③モデルの予測データの取得・可視化
モデルの予測データを得ます。
モデル名.predict("予測開始時","予測終了時")とすると予測データが得ることができます。
また、得られたデータを可視化します。
#predに予測データを代入
pred = SARIMA_MSFT.predict('2023-1', '2025-12')
#predと元の時系列データを可視化
#予測データは赤色で表示
plt.plot(df["Close"])
plt.plot(pred, "r")
plt.show()
元のデータと比較すると、予測データに若干の差異がありますが概ね合致しています。
また、2025年以降の株価は、上昇していくと予測しています。
会計システム等はインボイス制度や電子帳簿保存法等、税制改正により利用料は上がっていく印象がありますので、それらを反映して上昇していくのでしょうか。
6.終わりに
今回はSARIMAモデルを用いた時系列分析で株価予測を行いましたが、株価は時系列以外のファンダメンタル等の要素にも影響を受けているので、時系列分析だけで高精度の予測を行うことは難しいと感じました。
今後も学習を続けて他のモデルを試しさらなる分析にチャレンジしたいと思います。
