アンケート調査データにおけるバイアスを補正する取り組みについて

2023年1月20日 17:22

はじめに

こんにちは！株式会社グロービスのデジタル・プラットフォーム部門、データサイエンスチーム、データサイエンスユニットでデータサイエンティストとしてお仕事をさせていただいております伊藤です。
ビジネススキルを動画で学べる GLOBIS 学び放題というサービスについて、学習行動履歴データ（学習行動ログ）やアンケート調査データなどのデータ分析を担当しています。
今回は、アンケート調査データにおけるバイアスの補正に関する取り組み事例についてご紹介できればと思います。

GLOBIS学び放題におけるアンケート調査の取り組み

データサイエンスユニットでは、ユーザーのより良い学習体験を実現するためなどの目的で Web上やアプリケーション上でアンケート調査を定期的に実施しています。
アンケート調査を実施することで、学習ログからは把握できないサービスに対するユーザーの意見やニーズを集めることができます。
調査データを集計・分析し、分析結果に関する議論をステークホルダーと実施することで意思決定のための支援を行っています。

アンケート調査データにおける課題

アンケート調査で得られたデータについて分析を行う際に注意すべき課題は、調査で得ることができなかった欠測データ（調査非協力者のデータ）の存在です。
あるサービスを利用するユーザーに対して、アプリケーション上でサービス満足度に関するアンケート調査を一定期間実施する場合を例として考えます。
このとき、調査期間中にアプリケーションにログインしていない非アクティブユーザーはそもそも調査の回答者になることはありません。
また、サービスの内容に好意的で協力的なユーザーでないと調査の回答者にならない可能性が高いと考えられます。
上記の例のように、母集団から無作為抽出されていない集団において、回答者と非回答者間で集団としての性質が異なっていると考えられる場合、回答者から得られたデータの性質には偏りが生じます。
意図せず誤った分析結果をもたらさないためにも、上述した偏りに対して適切に対処した上でデータを扱うことが望ましいと考えられます。

傾向スコアを用いた選択バイアスの補正

選択バイアスを補正する基本的戦略

「本来対象とする集団」から一部の対象者が選択されている（あるいは脱落している）状況で、単純の解析を行うことで生じる結果のゆがみのことを選択バイアス[1]と呼びます。
選択バイアスの問題を欠測データの問題として位置づけた上で枠組みを拡張することで、調査データの偏りを議論できることが知られています。
例えば、ユーザーに対してアンケート調査を実施することを想定する場合、以下の図1の枠組みを検討することができると考えられます。

図1 : 欠測データにおける選択バイアスの考え方をアンケート調査データに拡張した枠組み
（星野(2009)をもとに筆者作成）

因果推論の手法の多くは、手持ちのデータに何かしらの重みを付けて妥当な比較を行います。[2]
したがって、既存の観測データに重みづけすることで関心のある目的変数についての正しい情報を手に入れようとすることが選択バイアスを補正する基本的戦略であるということができます。

傾向スコアの概要

傾向スコアとは、各ユーザーに対して介入が行われる確率を算出した0から1の値を取りうるスコアのことです。
アンケート調査の場合、介入ありの調査協力者のグループに所属する確率のことになります。
傾向スコアの値が1に近いほど調査協力者のグループに該当する確率が高まります。

調査データに傾向スコアを用いる意義

傾向スコアは調査回答者であるか否かを目的変数とし、共変量を説明変数として投入したモデル（例：ロジスティック回帰）の結果として求めることができます。
複数の共変量の情報をもとにした一次元の集約された指標ということができ、因果効果を推定することができるのが傾向スコアを用いる意義です。
調査データに対しても傾向スコアを用いた補正に関する研究事例が複数存在します。
前提や検討すべき諸条件はあるもののバイアスを補正する方法として検討される手法であるといえます。

傾向スコアを用いた選択バイアス補正手法の例

前述した表1の枠組みでデータ取得可能であることを前提として、今回は目的変数 Y（4件法によるアンケート結果）、共変量 X1~X3、介入変数 Z のデータについてバイアスを補正する例を簡単な実装とともに紹介します。
ここで4件法とは、調査における程度及び頻度の評定法に関する選択法におけるリッカート尺度で、回答者の意見や態度、実態の回答を4段階で求める方法のことです。
以下に4件法の具体例を示します。

4件法の具体例
- あなたは現在利用しているサービスにどの程度満足していますか。この中から1つだけお答えください。
  1. 満足である
  2. どちらかといえば満足である
  3. どちらかといえば不満である
  4. 不満である

今回のゴールは4件法によるアンケート結果について、バイアス補正前とバイアス補正後のデータ（図2）を得ることとします。

1. 補正先となる目標母集団を決定する
調査によって特徴を明らかにしたいバイアスの補正先となる目標母集団を決定します。
例えば、「有料化しているユーザー」や「1週間以内にログインしたユーザー」などが一例といえます。
補正先の母集団はビジネス的な観点も踏まえて妥当性を判断した上で目標母集団を決める必要があると考えています。

2. 調査の実施において目的変数、共変量の候補、介入変数を観測データから作成する
目的変数 Y における選択バイアスを補正する分析を行うために必要なデータを作成します。

目的変数 Y：ビジネスサイドやデータサイエンティスト側が興味・関心のある補正対象となる変数。
- 例：サービスに対する満足度の4件法によるアンケート結果など
共変量 X：目的変数 Y 及び介入変数 Z の両方と関連が強いと考えられる変数のうち、介入や目的変数よりも時間的に先行している変数。
- 例：性別・年齢などのデモグラフィックデータ、会員登録後からアンケートに答えるまでのサービス利用時間なとビジネスドメインをもとに作成された変数。
介入変数 Z：調査協力者 / 調査非協力者を区分する変数。どちらの群に割り当てられるかは観測された共変量のみに依存し、目的変数には依存しないという仮定を置く。
- 例：アンケート調査協力者 / アンケート調査非協力者

作成されるデータのイメージは以下の通りです。（pandas.DataFrame で目的変数 Y（4件法によるアンケート結果）、共変量 X1~X3、介入変数 Z (Z=1/0) のデータが以下の図3のようにそれぞれ存在することを前提とします。

3. 共変量の候補の中から共変量の選択を行い、共変量 Xi で介入変数 Z を予測するモデルを作成する
用意した共変量 X1～X3 を投入して介入変数 Z を予測します。
ここでは、ロジスティック回帰による予測モデルを構築します。
ロジスティック回帰の数式は以下のように表現できます。

$$
Z_i = σ(β\textbf{x}_i + u_i)\\
σ(\textbf{x}) = \frac{1}{1 + \exp^{-x}}\\
\hat{p}(\textbf{x}_i) = \hat{z_i} = σ(\hat{β}\textbf{x}_i)
\\
\\ Z_i:被験者iの介入変数
\\ β:推定されるパラメータ
\\ u_i:被験者iの誤差項
\\ σ:シグモイド関数
\\ \textbf{x}_i:被験者iの共変量の値
$$

今回は scikit-learn を用いてロジスティック回帰を実装します。[4]
実装例は以下となります。

# 必要なライブラリの読み込み
import pandas as pd
from sklearn.linear_model import LogisticRegression

# データの読み込み
df = pd.read_csv('sample_data.csv')

# 共変量をもとに回答者 / 非回答者を予測するロジスティック回帰モデルを構築する
# 共変量のリスト
covariate_list = ['covariate1', 'covariate2', 'covariate3']

# 説明変数の定義
X = df[covariate_list]

# 目的変数の定義
Z = df['answer_flg']

# ロジスティック回帰モデルの作成
model = LogisticRegression().fit(X, Z)

# ロジスティック回帰モデルにおける指標確認
for column, coef in zip(covariate_list, model.coef_[0]):
    display(f'{column}: {coef}')

display('intercept: ', model.intercept_[0])
display('accuracy: ', sum(model.predict(X)==Z)/len(Z))

# 出力結果例
# covariate1: 0.0339 # covariate1 の係数 B1
# covariate2: -0.0002 # covariate2 の係数 B2
# covariate3: 0.0001 # covariate3 の係数 B3
# intercept: -5.2768 # 係数α
# accuracy: 0.971 # モデルの精度

4. 予測モデルをもとに各サンプルにおける傾向スコアを求める
次にロジスティック回帰の結果をもとに各サンプルにおける傾向スコアを求めます。
傾向スコアの定義は Xi = (X1, X2, ,…, Xi) で条件付けた Zi＝1 の処置される確率です。
数式は以下のように表現できます。

$$
e_i ={P}(z=1|\textbf{x}_i) \\

\\ e_i:被験者iの傾向スコア\\ z:割り当て変数(処置群は1,対照群は0)\\ \textbf{x}_i:被験者iの共変量の値
$$

作成したロジスティック回帰モデルをもとに傾向スコアを算出することができ、model.predict_proba(X)[:,1] で取得することができます。
実装例は以下となります。

# df の propensity_score カラムに傾向スコアを格納
df['propensity_score'] = model.predict_proba(X)[:,1]

# 5件のデータにおける傾向スコアの確認
display(df['propensity_score'].head())

# 出力結果例
# 0.03 # 1人目の傾向スコア
# 0.04 # 2人目の傾向スコア
# 0.03 # 3人目の傾向スコア
# 0.02 # 4人目の傾向スコア
# 0.03 # 5人目の傾向スコア

5. 算出された傾向スコアを用いた逆確率による重み付けを行い、補正前と補正後の値を目的変数の割合を比較する
最後に算出された傾向スコアを用いた逆確率（逆数）による各調査回答者の重みづけを行います。
数式は以下のように表現できます。

$$
\hat{E}(y^{(1)})= \sum_{i=1}^{N} \frac{z_iy_i}{e_i}/ \sum_{i=1}^{N} \frac{z_i}{e_i}
\\

\\
e_i:被験者iの傾向スコア\\ z :被験者iの割り当て変数(処置群は1,対照群は0)\\ y_i:被験者iの観測できる結果変数
$$

重みづけのイメージは以下の図4のようになります。

図4 : 逆数によって重みをつけて本来の期待値に近づけるイメージ
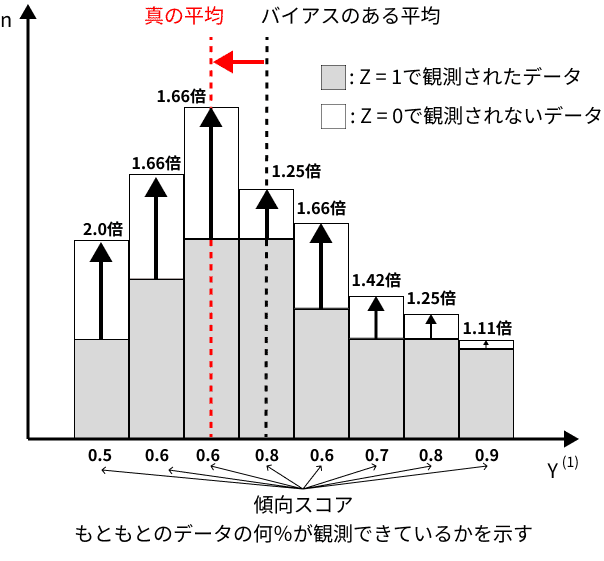
（安井(2020)をもとに筆者作成）

今回の目的変数 Y は4件法で取得されたデータであるため、回答の結果ごとにそれぞれ補正を実施をおこないます。
したがって回答の結果ごとに繰り返し処理を行う必要があります。
実装例は以下となります。

# 必要なライブラリの読み込み
import numpy as np
import functools as ft

# 4件法におけるアンケート結果の補正
index_list = [] # 4, 3, 2, 1 の値を格納するための空のリスト
score_list = [] # 重み付けされた回答結果の値を格納するための空のリスト

for i in np.sort(df['answer'].unique()): # 4件法における回答結果ごとに算出。4, 3, 2, 1
    if np.isnan(i): # 4件法における回答結果が not a number のものは除外
      continue
  
    # 変数iと同じ回答結果をおこなったユーザーの情報のみ抽出する
    df_target = df[df['answer'] == i]

    # 傾向スコアを用いた逆確率（逆数）による各アンケート回答者の重みづけされた合計値。各アンケート回答結果ごとに補正された回答人数を算出。
    weighted_num = sum(df_target['answer_flg'] / df_target['propensity_score'])

    # 回答結果iと重みづけされた合計値をリストに追加
    index_list.append(i)
    score_list.append(weighted_num)

# 補正前のデータフレーム
df_uncorrected_num = pd.DataFrame(df['answer'].value_counts().reset_index()).rename(columns={'index':'answer', 'answer':'uncorrected_num'}) # 補正前の回答人数
df_uncorrected_ratio = pd.DataFrame(df['answer'].value_counts(normalize=True)).reset_index().rename(columns={'index':'answer', 'answer':'uncorrected_ratio'}) # 補正前の回答人数の割合

# 補正後のデータフレーム
df_corrected = pd.DataFrame([index_list, score_list]).T.rename(columns={0:'answer', 1:'corrected_num'})
df_corrected['corrected_ratio'] = df_corrected['corrected_num'] / sum(df_corrected['corrected_num']) # 補正後の回答人数の割合

# 補正前と補正後のデータフレームを回答結果（answer）をキーに横ジョイン
df_result = ft.reduce(lambda left, right: pd.merge(left, right, on='answer'), [df_uncorrected_num, df_uncorrected_ratio, df_corrected]).sort_values('answer', ascending=False)

# 結果出力
display(df_result)

# 出力結果例
# answer uncorrected_num uncorrected_ratio corrected_num corrected_ratio
# 4.00 　14	　　    　　　0.48	　　　　　　457.51        0.45
# 3.00 　11	　    　　　　0.38	　　　　　　368.57        0.37
# 2.00 　2	　    　　　　0.07	　　　　　　97.54         0.10
# 1.00 　2	　    　　　　0.07	　　　　　　84.08         0.08

表2における補正後の出力結果（corrected_ratio）を取得することができました。
補正前と補正後で比較すると、補正された値は4, 3と回答した割合がそれぞれ3％, 1％減少し、2, 1と回答した割合がそれぞれ3％, 1％増加しています。
以上が傾向スコアを用いた選択バイアスの補正手法の一例となります。

バイアスを補正する難しさ

バイアスの補正に取り組んでみて感じた難しさは、補正がうまくいったのかどうかを確認する方法についてです。
従来調査 v.s. インダーネット調査の比較の枠組み【1】などある種の正解がある場合、誤差を算出する等で補正がうまくいったかどうかの答え合わせを行うことができますが、今回のように一時点でのアンケート調査ではそのような答え合わせはできません。
上記に関連してある調査では、補正方法における趣旨として、計測不可能な「正解」に近付くかどうかではなく、補正によってそれぞれの調査の分布・平均値がどのように変化するかである。[3]とされています。
バイアスが取り除かれた真値に近づくかだけではなく、調査設計と分析における手続きの妥当性を検証しながらデータ取得および分析手続きによる補正結果の知見を蓄積していくことが重要であると考えています。
調査データから得られる結果を過大・過少評価しないためにも、継続的にバイアス補正に取り組んでいきたいと思います。

今後の検討事項

よりよい補正結果を取得するために、以下のような内容を今後の検討事項として考えています。

補正先の目標母集団をどのように決定するかについての検討
共変量をどのように選ぶかに関する検討
- 強く無視できる割り当ての前提を成り立たせるための十分な共変量が用意されているかの検証（未観測の共変量について）
- 目的変数と相関がありそうな変数をどのようにして見つけるかに関する調査（共変量の選択について）
モデルをどのように選ぶかに関する検討
- 共変量選択の方法
- モデルの種類の変更
- パラメータチューニングの実施
その他
- 傾向スコアを用いた逆確率による重み付け以外のバイアス補正方法の検討

終わりに

今回はアンケート調査データの補正に関する事例を紹介しました。
バイアス補正結果については絶対的な正解があるわけではありませんが、調査結果を鵜吞みにせず統計的因果推論の手法に基づいてバイアスと向き合うことが重要であると感じています。
今後もバイアス補正にとどまらない統計的因果推論の手法の検討と実装を実施していきたいと考えています。
今回ご紹介したような傾向スコアや IPW を用いたバイアス補正の方法は、様々なデータに応用できます。
調査データをエビデンスとしてビジネス上の意思決定に貢献したい方は、是非バイアス補正にトライしてみてください!

参考文献

【1】星野崇宏(2009). 『調査観察データの統計科学　因果推論・選択バイアス・データ融合』. 岩波書店.
【2】安井翔太(2020). 効果検証入門　正しい比較のための因果推論／計量経済学の基礎』株式会社ホクソエム監修, 技術評論社.
【3】谷口翔紀・大森翔子(2022). 『インターネット調査におけるバイアス：国勢調査・面接調査を利用した比較検討』公益財団法人 NIRA 総合研究開発機構.
【4】scikit-learn developers(n.d.).『1.1. Linear Models』. https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression.predict_proba , (2023年1月23日アクセス)
【5】Pedregosa et al. (2011). 『Scikit-learn: Machine Learning in Python』JMLR 12, pp. 2825-2830.

グロービスで一緒に働くデータサイエンティストを募集しています！

グロービスのデータサイエンスチームでは、一緒に働けるデータサイエンティストを探しています！まずは、カジュアル面談を通して、あなたに合う組織かどうか確かめてみませんか？
https://recruiting-tech-globis.wraptas.site/