16 Visualizing uncertainty in Japanese あいまいなデータの可視化
原文はこちら
Introduction
データというのは実はあいまいだ。そのデータポイントははたして正しいデータだろうか。可視化をする前に、データの検証は決してかかせない。
あいまいさを解消する一般的なアプローチはエラーバーと信頼区間(error bar and confidence band)だ。
(訳注)Uncertainty は直訳すると「あいまい」だが、統計的には「不安定」とされ、具体的には分散(その平方根である標準偏差)が大きいことをさす。
16.1 Framing probabilities as frequencies 確率を頻度としてフレーミングする
不確実性とはなにか
未来の事象:コインを投げたとして、その結果が表か裏か
ちなみに過去についても、例えば朝には駐車場にあったある自動車が昼にはなかったとしたら、出発していたことになるが、いつ出発したかは不確実
数学的には確率(probability)という概念を用いる
確率という概念はそうとうに難しいが、実際のところ頻度(frequency)について考えればじゅうぶん
あるランダムな試行(trial)、たとえばコインをなげるとかサイコロをふるとかして、特定の結果、表がでる・6の目がでる、を成功とよび、これ以外を失敗とする。成功の確率はこの試行を繰り返した結果、成功の頻度/試行数 で表現できる。
Fig 16.1 はこの頻度を可視化したもの
不連続な結果の可視化(discrete outcome visualization)とよばれる
目をつむって、このうちどれかのマスをタッチしたときに、黒いマスにあたる確率ととらえるとわかりやすい

結果が連続型の変数(Continuous Variable / Numeric Variable)の場合もある
例えば選挙。政党が青色政党と黄色政党があり、青色政党が1ポイント(1%)支持率が高く、その誤差が1.76ポイントあるとする。
黄色政党が逆転する場合もあれば、青色政党がさらに差をつけることもあるだろう。
こうした起こりうる結果の範囲とその尤度を表したものを確率分布(probality distribution, Fig 16.2)とよぶ。Chap 7も参考。

Fig. 16.2を見ると黄色が勝つ確率は12.9%ある。Fig 16.1の10%を見るとより分かりやすいかもしれない。
あなたが青色の支持者だとしたら、完全には安心できないと思うだろう。
我々は確率を理解するのは難しく、離散型の表現のほうがわかりやすい。(訳注:こちらの本がおすすめ!)
Fig 16.1 と、Fig 16.2 を組み合わせることもできる。
これを quantile dotplot とよぶ(Kay et al. 2016)

このプロットはドットの数が多すぎないほうがよい。
Fig 16.3 a はドットの数は50個。より正確に青や黄色の勝つ確率を表している。
bは10個のドット。こちらのほうが、それぞれの確率をより視覚的に判別しやすい
批判があるとしたら、正確ではないこと。
数学的に正確であっても、適切に認識されない(わかりづらい)可視化は実用的ではない。
16.2 Visualizing the uncertainty of point estimates
統計学、標本推定の基本
統計学の目標: ちいさな標本から世界全体について知ること
少数のサンプルから、それぞれの選挙区の青・黄の投票割合を知る
全数調査はできないので、ランダムにサンプリングした結果から、全数調査の結果を推定する。
全数のことを母集団(population)とよび、調査のための小さな集団のことを標本(sample)とよぶ。
以下、用語の整理
母集団の平均値や割合など:母数(parameter)
一般に、知ることはできない
標本の平均値や割合:推定値(estimate)
調査や実験について知ることができる
平均値などのように特定の値の推定値は点推定値(point estimate)とよぶ
Fig 16.4
関心のある変数(投票結果など)の母集団の分布と標準偏差
サンプル(標本)は特定の観測値の集合であり、その観測値の数はサンプルサイズとよばれる
サンプルでも分布、平均、標準偏差を計算できるが、その数値は母数とは一般的に異なる。
標本分布の幅は標準誤差と言われ、サンプルサイズが大きくなるほど小さくなる。

標準偏差と標準誤差を混同しないことが重要。
標準偏差は個々の観測値のばらつきを示し、母集団の特性です。
標準誤差は、母推定の精度
統計学者はサンプルを使用してパラメータの推定とその不確実性を計算しますが、そのアプローチにはベイジアンと頻度主義者の二つ
ベイジアンは事前知識を持ち、サンプルでその知識を更新
頻度主義者は事前知識なしに世界について正確に記述
不確実性を視覚化する際には、両者は一般的に同じ戦略を使用
頻度主義者は主にエラーバーを使って不確実性を視覚化します。
エラーバーは有用ですが、何を表しているのか読者に誤解を招きやすい。
Fig 16.5: あるデータセットに対する誤差棒の異なる5つの使用例

Whenever you visualize uncertainty with error bars, you must specify what quantity and/or confidence level the error bars represent.
不確かさをエラー・バーで可視化する場合は常に、そのエラー・バーがどのような量や信頼レベルを表すかを指定する必要がある。
標準誤差は、サンプルの標準偏差をサンプルサイズの平方根で割ることで求められる。
信頼区間は、標準誤差に小さな定数値を乗じることで計算されます。
例えば、95%の信頼区間は平均から標準誤差の約2倍の範囲に拡がる
サンプルサイズが大きいほど、同じ標準偏差でも標準誤差と信頼区間が狭くる
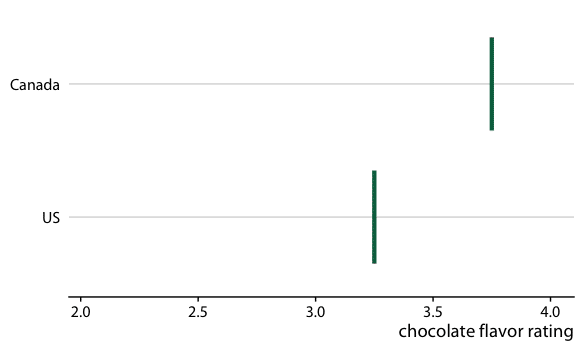
カナダとスイスのチョコレートバーの評価を比較するとこの効果が見られます。
カナダのバー125個、スイスのバー38個の評価があり、カナダとスイスのチョコレートバーの平均評価とサンプル標準偏差は似ていますが、信頼区間はスイスのバーの方がはるかに広い。

Fig 16.6では、信頼度の低い区間を表すために、より濃い色と太い線を使用して、同時に3つの異なる信頼区間を示す。
これらの視覚化を「graded error bar」と呼ぶ。グレーディングは、異なる可能性の範囲を読者に認識させるのに有用。
もしグレーディングされていない単純なエラーバー(グレーディングなし)を群衆に見せた場合、少なくとも何人かはエラーバーを誤解する。
たとえば、データの最小値と最大値を表していると考えるかも。
また、エラーバーが可能なパラメータ推定の範囲を示しており、推定が誤差棒の外に出ることはないと考えるかも。
これらの誤解は「deterministic construal errors」と呼ばれる。
deterministic construal errorsのリスクを最小限に抑えるようにすると、不確実性の視覚化が向上する。
エラーバーは、多くの推定値とそれらの不確実性を一度に示すことができる。そのため、専門家向けの大量の情報を伝えることが主目的である科学出版物で一般的に使用されている。
このタイプの応用の例として、Fig 16.7 は6つの異なる国で製造されたチョコレートバーの平均評価と関連する信頼区間を示している。

図16.7を見ると、平均評価の違い
カナダ、スイス、オーストリアのバーの平均評価はアメリカのバーの平均評価より高い
これらの平均評価の不確実性を考慮すると、平均の違いは有意なのか。
「有意」という言葉は統計学者が使用する技術的な用語です。ある信頼水準で、観測された違いがランダムなサンプリングによるものだという仮定を棄却できる場合、その違いを有意と呼ぶ。
平均評価に違いがあるかどうかを正しく評価する方法は、差の信頼区間を計算すること。
これらの信頼区間がゼロを除外している場合、その信頼水準で差が有意である。
(訳注:一般に帰無仮説有意性検定は図からは行わない)
チョコレート評価データセットでは、カナダのバーだけがアメリカのバーと比べて有意に高い評価(図16.8)。
スイスは95%信頼区間にふくまれるので有意ではない。オーストラリアも同様。

Fig 16.9 様々なエラーバー
a, c(キャップ付き)と図16.9b, d(キャップなし)
graded error bar は、異なる信頼水準に対応する異なる範囲の存在を強調しますが、追加情報の反面として視覚的なノイズが増加。
図の複雑さや情報密度によっては、シンプルなエラーバーの方が好まれる。
エラーバーにキャップを付けるかどうかは主に個人の好みの問題です。
キャップが付いている場合(図16.9a, c)、どこで終わるがを明確。
キャップがない場合(図16.9b, d)、信頼区間の全体範囲を強調。

Confidence Band (e, f) はわかりづらいのでやめよう。
シンプルな2D図では、エラーバーは多くの他のプロットタイプと組み合わせやすいため、科学出版物で一般的に使用る。
例えば、エラーバー付きの棒グラフや散布図(図16.10、16.11)で不確実性を示すことができる。


頻度主義者とベイジアンのアプローチの違いについて考えよう。
ベイジアンは真の値(母数)がどこにあるかを探す
頻度主義者は真の値がどこにないかを探す
ベイジアン:データと事前知識をつかって、母数がどのように分布するかを計算
頻度主義者:帰無仮説をたて、データがランダムではない場合いほど帰無仮説から離れている、確率を計算する。
Fig 16.2?

ベイジアンの信頼区間は真のパラメータ値についてのもの、、頻度主義者の信頼区間は帰無仮説についてのもの。
実際には、ベイジアンと頻度主義者の推定値はしばしば似ている(Fig 16.13)。
ベイジアンアプローチの概念的な利点は、効果の大きさについて考えることを強調する点。
一方、頻度主義者の考え方は効果が存在するか否かの二元的な視点。

A Bayesian credible interval answers the question: “Where do we expect the true parameter value to lie?” A frequentist confidence interval answers the question: “How certain are we that the true parameter value is not zero?”
ベイジアン推定の中心的な目標は事後分布を得ること。
そのため、ベイジアンは信頼区間に単純化するのではなく、分布全体を視覚化することが一般的。
データの視覚化において、第7章、第8章、第9章で議論された分布の視覚化のすべてのアプローチが適用可能。
具体的には、ヒストグラム、密度プロット、ボックスプロット、バイオリンプロット、リッジラインプロットがベイジアンの事後分布の視覚化に一般的に使用される。
これらのアプローチは特定の章で詳しく議論されているため、ここではリッジラインプロットを使った一つの例を示す。
この例では、チョコレートの平均評価に関するベイジアンの事後分布を示しており、カーブの下にシェーディングを追加して、定義された事後確率の領域を示す。
シェーディングの代わりに、量子ドットプロットを描くこともできたし、各分布の下にグレーデッド誤差棒を追加することもできたでしょう。リッジラインプロットに誤差棒が下にあるものは「ハーフアイ」と呼ばれ、バイオリンプロットに誤差棒が付いているものは「アイプロット」と呼ばれます(第5.6章)。

16.3 Visualizing the uncertainty of curve fits 不確実性を曲線にフィットさせる
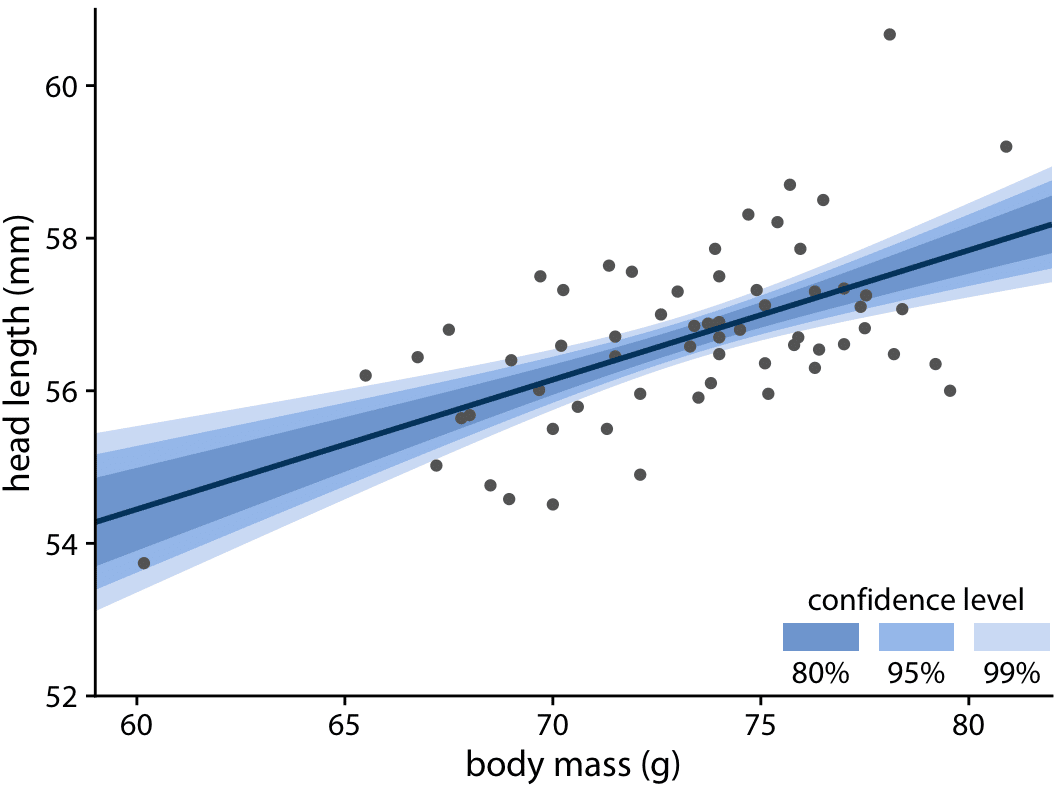
第14章では、データに直線や曲線をフィットさせることでデータセットのトレンドを示す方法について議論。これらのトレンド推定にも不確実性があり、トレンドラインの不確実性を信頼バンドで示すのが一般的(Fig 16.15)。
信頼バンドは、データと互換性のあるさまざまなフィットラインの範囲を示す。
信頼区間が湾曲している理由は理由は、直線フィットが二つの異なる方向に動くことができるため:上下に移動する(つまり、異なる切片を持つ)ことと、回転する(つまり、異なる傾きを持つ)こと。
信頼バンドがどのように生じるかを視覚的に示したものがFig 16.16


信頼帯を描くためには、信頼水準を指定する必要がある。
Fig 16.17 :Graded Confidence Level。
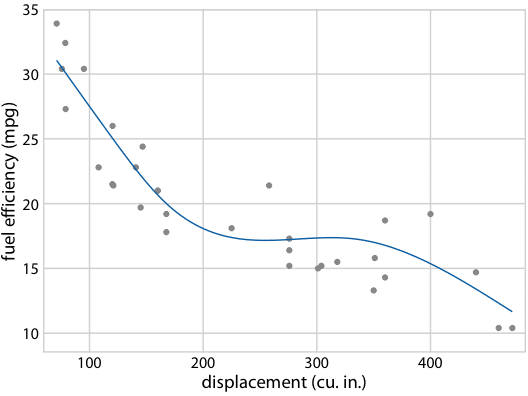
非線形カーブフィットに対しても信頼バンドが描ける(Fig 16.18)。
bが明らかにするように、信頼バンドはかなりウィグリー(ねじれたり曲がったりする)特性を持つカーブの一軍。

16.4 Hypothetical outcome plots (HPO, 仮説出力プロット)
静的な不確実性の視覚化は、視聴者がデータの確定的な特徴と誤解するリスクがあります(決定論的構想エラー)。
?All static visualizations of uncertainty suffer from the problem that viewers may interpret some aspect of the uncertainty visualization as a deterministic feature of the data (deterministic construal error)
この問題を避けるには、異なるが等しく可能性のあるプロットを順番に表示するアニメーションによる視覚化が有効。
この方法を仮説的結果プロット(HOP)と呼びます。
オンライン環境やプレゼン場面でのアニメーションとして効果的に使用できる。
チョコレートバーの評価に関する例。
カナダ製とアメリカ製のチョコレートバーをランダムに選んで比較し、その結果を繰り返し記録。
このプロセスを可視化し、各抽出での2つのバーの相対的なランキングを示します。

原文参照
https://clauswilke.com/dataviz/visualizing-uncertainty.html
第二の例として、Figure 16.18bにおける同等に可能性のあるトレンドラインの形状の変動を。全てのトレンドラインが重ねてプロットされているため、主にトレンドラインによって覆われる全体的な領域が認識されますが、個々のトレンドラインを識別するのは困難です。
この図をHOPに変換することで、一度に一つのトレンドラインを強調表示することが可能になり、各トレンドラインの個別の特徴を明確に示すことができます。

HOP(仮説的結果プロット)のポイント:
アウトカム間の切り替え方:
結果を瞬間的にに切り替えるか、滑らかにアニメーション化するかを選ぶ必要がある。
滑らかな遷移は確率の判断を難しくすることがあるため、アニメーションは速やかに行うか、フェードイン・アウトのスタイルを選択するのが良い。
結果の代表性:
示される結果が可能なアウトカムの真の分布を代表していることを確認する必要がある。
そうでないと、HOPは誤解を招く可能性がある。
例えば、チョコレートの評価で米国製バーがカナダ製バーを上回る結果が多い場合、誤って米国バーの方が評価が高いという印象を与えてしまうかも。
この問題を防ぐためには、非常に多くのアウトカムを選択するか、示されるアウトカムが適切であることを何らかの形で検証しておく。
