13 Visualizing time series and other functions of an independent variable

Tacchan

原文はこちら


前章が２つの量的データの関係性を見るものだったが、そのうち一つが時間に関するものだったらどうだろう。時系列データは特殊な構造をもつ。

13.1 1つの時系列 Individual time series

  • Y軸：生物学でのオンラインで投稿された査読前論文の数

  • X軸：年月

  • 散布図と折れ線グラフの比較

    • 一般的な散布図との違い、時系列の散布図はX軸が等間隔かつ決められた順序（時間経過）ごとにならんでいること


  • 折れ線グラフには批判もある。それは実際の観測値ではない。

    • 観測してみたら右肩上がりではなく、V字だったということもあるかも

    • 線はあくまで「見やすくするためのもの」

  • 時系列の観測値が多い場合、ドットをなくすことも多い。視覚的にビジーではなく見やすくなるからだ*1

  • 全体的な傾向を示すにはラインの下を塗りつぶすのも有効

    • 面積が広がっているのを見やすいから

    • Y軸が0で固定されていて面積の高さが大きくなっているのが見やすいといい

13.2 複数のデータがあるとき Multiple time series and dose–response curves

  • 時系列にしたがう複数のデータがあるとき、プロットの仕方を考えよう

  • 散布図は見づらい


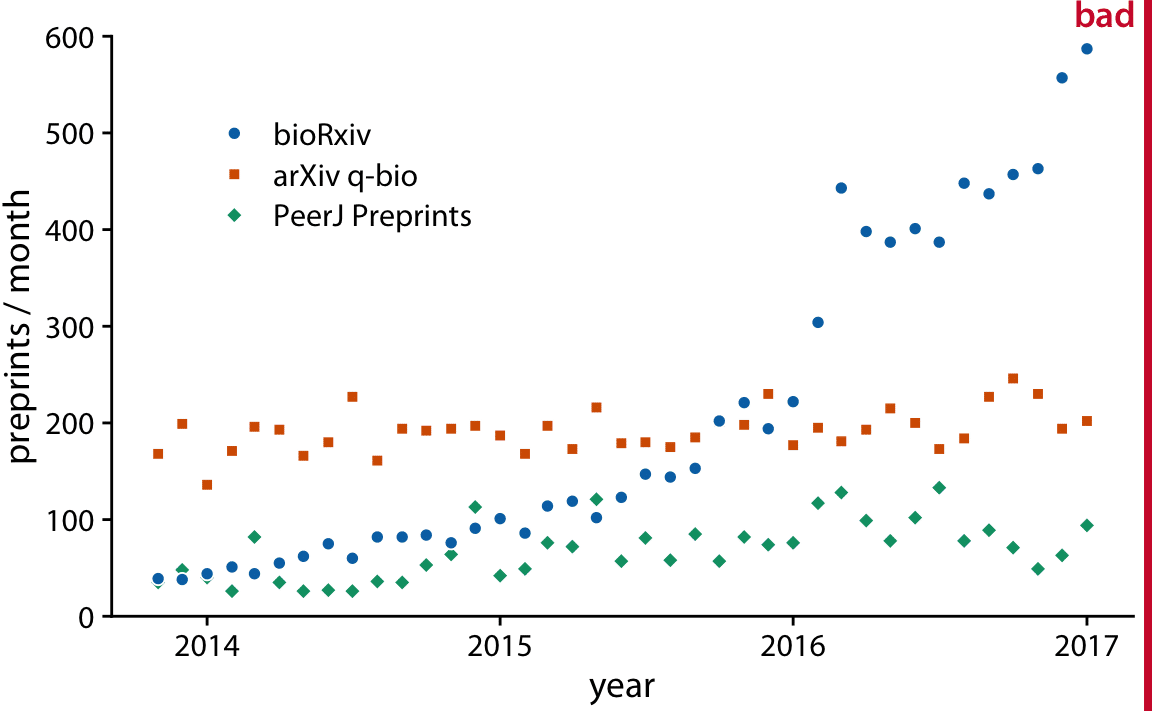
Fig 13.6はまあいいが、凡例やドットは認知負荷をたかめる。消してみるとみやすくなる



  • 折れ線グラフは時系列データではなくとも使える。

  • X軸のデータポイントが規則的であればいい

  • たとえば、用量-反応曲線

    • Fig 13.8 は1エーカーあたりの肥料量（X軸）ごとの、1エーカーあたりのオーツ麦の収穫量をしめす。

    • オーツ麦の種類にかかわらず、肥料の使用が収穫を増やしていることがわかる。


13.3 2つ以上の応答変数があるとき Time series of two or more response variables

  • これまでは1つの応答変数のみ扱ってきたが、こうしたケースはまれで、2つ以上の応答変数があるほうが一般的

  • たとえば、過去12か月の住宅価格の変化と失業率について考えてみよう。

  • 一般に住宅価格が高い場合失業率は低く、またその逆も同様だ。

  • これをグラフにした場合、Fig. 13.9 のように、2つのラインチャートを並べることができる。

    • ただし、これは特定の時期に2つのデータが同じように（あるいは逆方向に）変化しているか、といった比較が難しい。

  • 別の方法

    • ２つの変数の散布図をつくり、となりあうドットをつなげたもの

    • 物理学者やエンジニアはこれを Phase Portrait (位相レポート) とよぶ

      • 位相空間の動きを可視化するのにつかわれるため

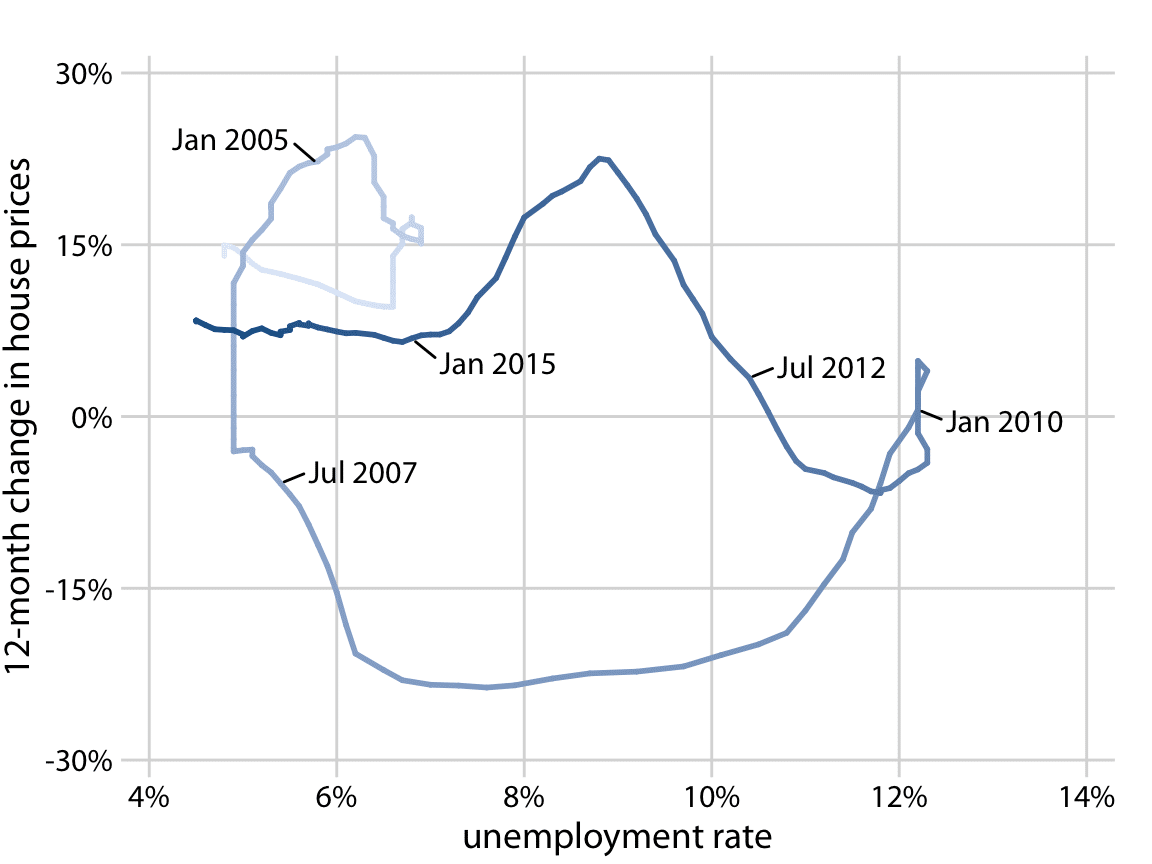
Figure 13.10 12か月間の住宅価格の変動と失業率を、2001年1月から2017年12月までプロットしたもの。線の色が濃いほど年次が新しいことを示す。住宅価格の変動と失業率が負の相関の場合、このチャート反時計回りに動く。

  • 位相レポートにおいて、線が左下から右上に描かれている場合、２つの変数が正の相関をたどったことをしめす（一方が上がれば、もう一方もあがる）

  • 対して、線が左上から右下に描かれている場合、負の相関（一方が上がれば、一方が下がる）を示す。

  • 散布図を結合したプロットの場合、（相関の）方向性と時系列の双方を示していることが重要。

    • それがない場合、たんなる落書き（Figure 13.11）になる。

    • Figure 13.10 では線にグラデーションをつけた色で方向性を示している。

  • Connected Scatter Plot は不規則なパターンが発見しやすい。

    • 事実、Figure 13.10 での反時計回り（住宅価格は上がっているが、失業率は下がっている）のプロットがこれを示している

  • これは最初は読み取り方にとまどうが、慣れると効果的なツールだ。


  • 次元削減を行えば、多数の変数をもつものの関係も可視化できる。

  • 以下の図は100以上の指標があるデータにたいして主成分分析（Principal Component Analysis, PCA）を行いプロットした。


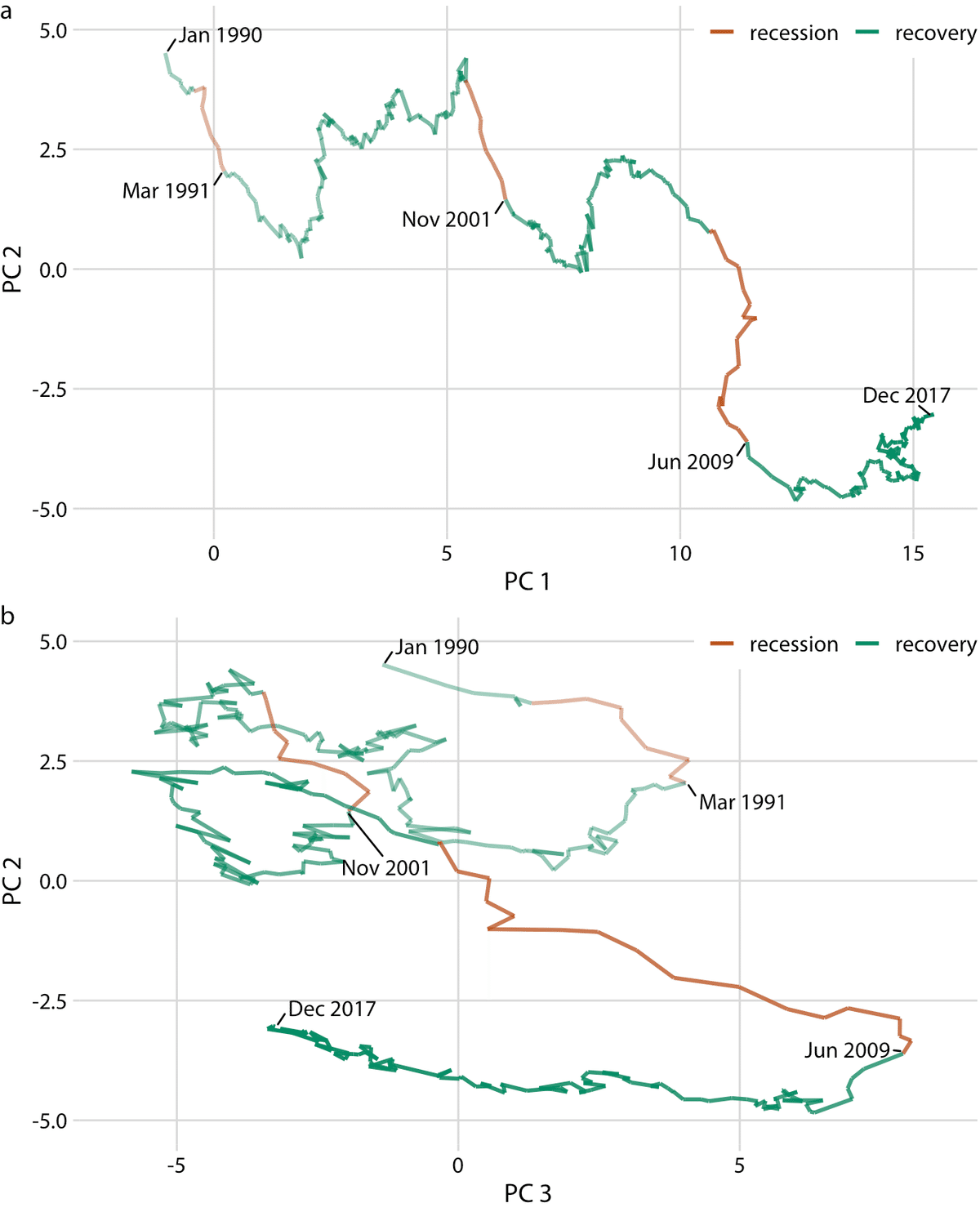
Figure 13.12：主成分空間におけるConnected Scatter Plotとして高次元の時系列を可視化したもの。パスは、1990年1月から2017年12月までの100以上のマクロ経済指標の共同の動きを示している。景気後退と回復の時期は色で示され、3つの景気後退（1991年3月、2001年11月、2009年6月）の終点もラベル付けされている。(a) PC 2 対 PC 1 (b) PC 2 対 PC 3。

  • Figure 13.12 a （上）：PC1（第一主成分）は経済規模を示す。これは一般的に年次ごとに拡大する。景気後退と回復で色分けしてみると、後退はとくに第2主成分と関連していそうだ。

  • Figure 13.12 b（下）：全体的に時計回りの変化をしている。これは景気の後退の後に回復があり、そしてまた後退があることがわかる。



訳注

*1 Tableauのデフォルトもこれ

メモ・気づき

  • object は動詞で「反対する」「意義をとなえる」

  • この文の意味がまったくとれない。倒置法の仮定法過去完了をつかっている、くらいしかわからない

    • In particular, if there are only a few observations spaced far apart, had observations been made at intermediate times they would probably not have fallen exactly onto the lines shown.

  • Overarching trend: 全体的な傾向

  • エリアチャート: Y軸が0でなくとも、固定されていればいいのでは？

  • Multiple time series: 時系列データが複数ある（問い合わせ日時と解決日時）のではなく、時系列データは１つで、それに呼応するデータが複数ある時

  • Dose-Responsive Curve: 容量反応曲線。

  • cwt: ヤードポンド法の質量単位。アメリカでは100ポンド（45.359237 kg）で 1cwt

  • vice versa: その逆もまた同様

  • cumbersome: 面倒

  • Phase Report: 位相レポート。正直、さっぱりわからない

  • perpendicular: 垂直

  • scribble: 落書き


いいなと思ったら応援しよう！