
これでマスター数学的考察編〜AtCoderを戦うために典型問題を徹底マスターしよう![競プロ解説]〜
数学的考察とは
数学的考察とは、「二分探索」「bit全探索」「累積和」などのような具体的なアルゴリズムではありません。数学的考察とは、競技プログラミングで出題されるような数学的感覚を必要とする問題を解く際のコツ、重要な視点をまとめた総称のようなものと言えるでしょう。
しかし、「数学的感覚を必要とする問題」と言われると、とても抽象的で、天才しか手の付けられない代物のような気がしてなりませんね。僕もそう思います。ですが、そのような典型問題として落とし込みにくいような問題たちでさえも、これから紹介する、体系的にまとめられた幾つかのコツを用いることで解法への糸口をつかむことができます。どう手を付けたら良いか全く分からない状態よりかは、遥かに問題を解く上で有利となるでしょう。
ですが、大前提として、まず初めに全探索で処理する方法を考えてみて下さい。全探索でも十分処理時間が間に合う場合(10の7乗程度)は、問題を解くという観点から見れば、数学的考察を行う必要がないかもしれないからです。
それぞれの数学的考察についての詳しい説明
数学的考察を行う上で有効な視点として、以下のようなことが挙げられます。
パリティ(偶奇)に着目する
とりあえず手を動かして法則性(規則性・周期性)を見つける
上界を考える
不変量に注目する
変数が減らせるか考える
剰余(mod)を考える
では、上で挙げたそれぞれの項目について、これから詳しく説明をしていきたいと思います。
パリティ(偶奇)に着目する
以下の記事の説明がとても分かりやすいです。
とりあえず手を動かして法則性(規則性・周期性)を見つける
とりあえず手を動かしてみると、ある一定の周期性を見つけることができる場合があります。以下の記事が参考になります。
上界を考える
最大値を求める問題では、「≤」のように上界を考えてみることで解ける場合があります。以下の記事が参考になります。
不変量に注目する
ある操作を「K回以内行う」とか「好きなだけ行う」とか指定されている問題は、操作ごとに不変なものを考えてみると特徴を捉えられる場合があります。
変数が減らせるか考える
例えばA、B、Cという値が入力として与えられる場合、A、Bのみについて考えれば良かったり、CをAもしくはBによって表せたりする問題などもあります。
剰余(mod)を考える
あまりに着目すると、ある周期性を見つけられるような問題があります。また、modの性質を知っていれば解くことのできる問題などもあります。
ここで、E869120さんが以下の記事で紹介していたとても分かりやすい図を掲載させていただきたいと思います。
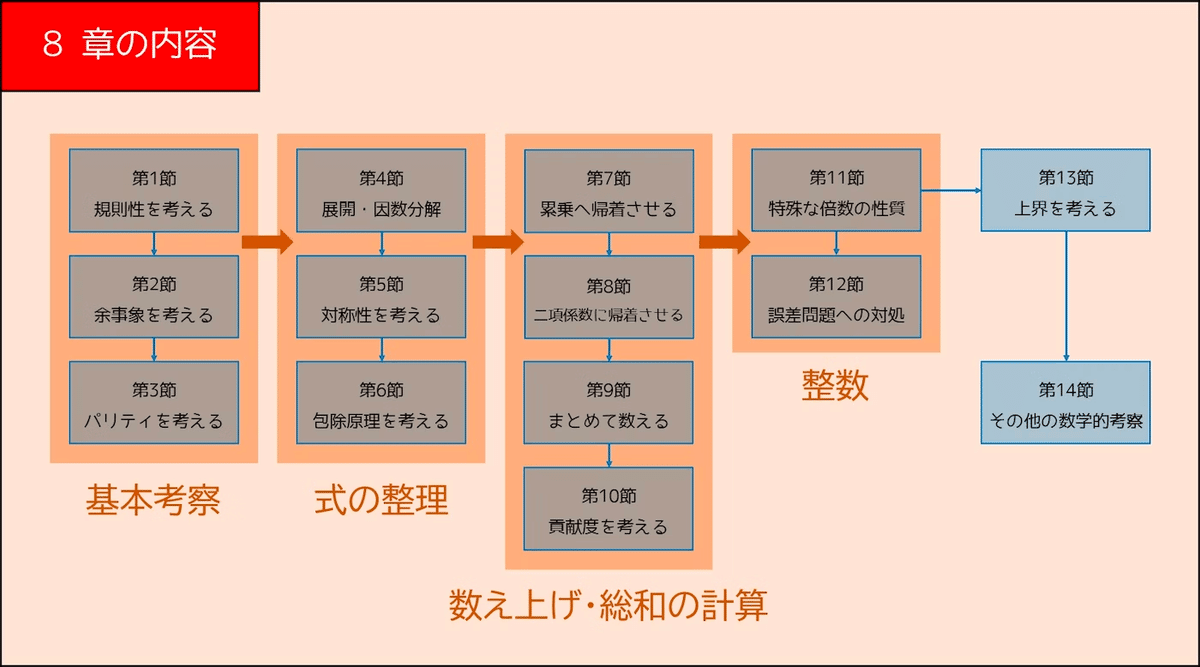
その他コラム
正直に言うと、数学的考察についてまとめることはかなり難易度が高いと私は思います。まず初めに、どのような項目に絞って紹介すべきかが悩みどころとなります。あまりに多くの数学的考察を紹介したところで、それら全部について理解し、それらを使いこなすにはとても労力が必要となります。あまりに多くのことについて紹介してしまったことで、結局頭の中が混乱し、どれも使いこなせなかった、と言うことにはしたくありません。そこで私は、ある程度は切り捨てて、より重要と思われる6つに絞って紹介してみました。今回紹介した記事の中には、他にもたくさんの項目について紹介し、とても分かりやすく解説している記事があります。そういった他の記事も読むことで、学びを深めていくことはとても面白いことだと思います。
練習問題
パリティ(偶奇)に着目する
とりあえず手を動かして法則性(規則性・周期性)を見つける
上界を考える
不変量に注目する
変数が減らせるか考える
剰余(mod)を考える
他にも、「アルゴリズムと数学 演習問題集」と言う問題集があり、多くの問題が紹介されているので、興味があったらぜひ解いてみてください。
参考文献
(スペシャルサンクス)
(その他)
いいなと思ったら応援しよう!

