
#07 Rational Function はこれで完璧!
皆さんこんにちは!
突然ですが、今回は IB Math AA のシラバスに含まれている Rational Function(有利関数)についてまとめます。
一次関数や三角関数などに比べて rational function はグラフの概形をイメージしづらく、あまり馴染みがない人もいると思いますが、実は IB Final で出題されるパターンは限られているのでマスターしやすい分野となっています。そのうえ、大きな得点源となる可能性があるので、ぜひ迷わずに素早く解けるようになってほしいと思い、記事を書くことにしました。
今回紹介する内容は主に Math AA に焦点を当てていますが、Math AI にも共通して言える部分もあると思うので、もしよかったら参考にしてみてください。特に Math AA HL を選択している人は、November 2021 の Paper 2 で 11 marks(全体の10%)を占める問題が出たこともあるので必見です!
今後も機会があれば、このように IB の各教科で扱う内容についての記事も書いていこうと考えているので、取り上げてほしい分野があればぜひリクエストフォームを送信してください!また、もしも誤植を発見した場合はご報告くださると助かります。
今回の進め方
IB Math AA のシラバスに含まれている rational function は、実はHLでもたったの3種類しかありません。その3種類とは、
Linear/Linear(一次式分の一次式)
Linear/Quadratic(二次式分の一次式)
Quadratic/Linear(一次式分の二次式)
です。SLで扱われるのは Linear/Linear のみで、後の2種類はHL範囲となっています。基本的にそれぞれの関数の概形がしっかり描けるようになれば問題ないので、今回はあくまでこれをメインに説明します。これから先、それぞれのパターンについて具体例の確認から始め、次に一般(ルーティン)化を行い、少し応用的な内容も含めて補足する、という流れで進めていきます。
Linear/Linear の形の攻略法は?【SL】
Linear/Linear の具体例

Linear/Linear のグラフは、vertical asymptote と horizontal asymptote がそれぞれ1本ずつあるので、まずはそれらを求めていきましょう。
Vertical asymptote は f(x) が ±∞ に発散してしまう、つまり定義されないところで発生します。Rational function の場合は、分母=0 となるような x の値を求めることで簡単に出せます。今回の場合だと、2x-1 = 0 より x = 1/2 が vertical asymptote となります。
よく見ると、既に x ≠ 1/2 という式が与えられているので、わざわざ自分で計算しなくても vertical asymptote は一瞬で求められます。多くの場合、vertical asymptote を問う問題は "state" や "write down" といった command term で配点が 1 mark となっているので、単に "x = 1/2" と回答するだけで点がもらえます(時間短縮)。ただし、vertical asymptote を問われているときは "x = __" の形で回答する必要があるので、間違っても "1/2" や "x ≠ 1/2" と書かないように!
次に horizontal asymptote ですが、これは x が ±∞ に近づいたときに f(x) が収束する値なので、次のような計算によって求められます:

今回の関数の場合は、このように horizontal asymptote が導けます:

Asymptotes がすべて求まったら、intercepts を求めていきましょう。
y-intercept のほうが求めるのは簡単で、単に f(0) の値を計算すれば良いだけです。この関数なら x=0 を代入すると f(0) = -2 となります。
x-intercept は f(x) = 0 という x についての方程式を解けば求まります:
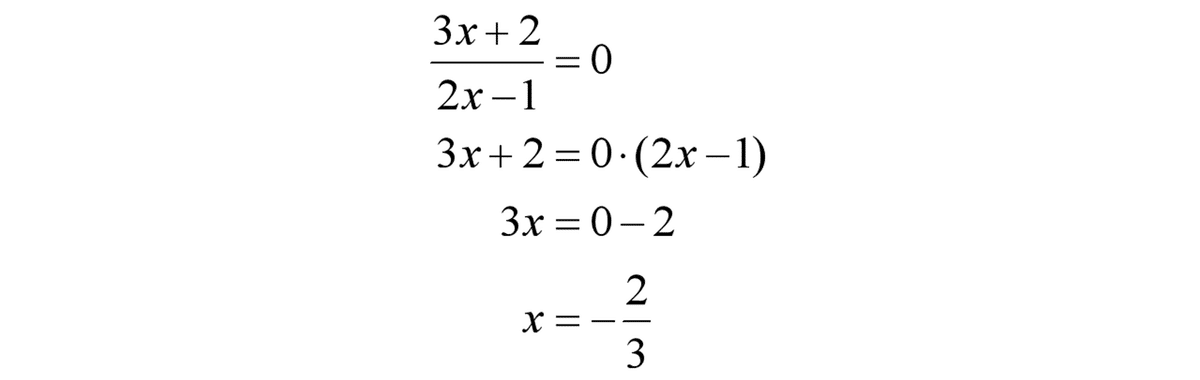
これらの情報をx-y座標上に表記すると、こうなります:

あとは、intercepts を通り、asymptotes と交わらずに近づく曲線を描けば完成です。Linear/Linear の場合は双曲線となる点に注意しましょう。

Linear/Linear の一般化
Linear/Linear の rational function は一般的に

という形で表すことができます。この時、上の例と同様に考えると

と求めることができます。特に順番が決まっているわけではないので、出題順に求めていけば問題ありませんが、もし特に誘導なしでグラフを描く必要が出てきた場合はルーティンに沿って進めるのが安全です!
Linear/Linear の補足
Rational function には、このような形の関数も含まれます:

この場合、通分して一つの分数に変形すると

と書き換えられるので、一旦見慣れた形に直すのが無難です。また、先ほどの手順通りに描けば気づくと思いますが、この場合のグラフは vertical asymptote と horizontal asymptote の交点の左上と右下に来ます。
Linear/Quadratic の形の攻略法は?【HL】
Linear/Quadratic の具体例

Linear/Quadratic でも基本的な流れは Linear/Linear と同じなので、サクサク進めていきましょう。
まずは、分母=0 を解いて vertical asymptote(s) を求めます:

この場合、x=-3/2 と x=7/2 の2つが vertical asymptotes となります。Linear/Quadratic の場合は、基本的に vertical asymptotes は2本あります。
次に horizontal asymptote について、x を ±∞ に飛ばすと

となるため、y=0 が horizontal asymptote となります。
y-intercept に関しては、f(0) = 1/3 となり、x-intercept は分母を払うと -4x+7 = 0 を解けばよいだけになるので、7/4 とこちらも簡単に求まります。
これらの情報をx-y座標上に表すと、

こんな感じになります。あとは、それぞれの区間で f(x) が positive か negative か、ということに注意しながらグラフを完成させるだけです。
今回の場合、例えば f(-2) を求めると -15/11 となり、左の vertical asymptote より左側では曲線が x-axis より下になることが分かります。また、例えば x=10 を代入すると分母・分子ともに negative になるため、f(x) は positive となり、右の vertical asymptote より右側では曲線が x-axis より上になることが分かります。このようにして完成したグラフはこちらです:
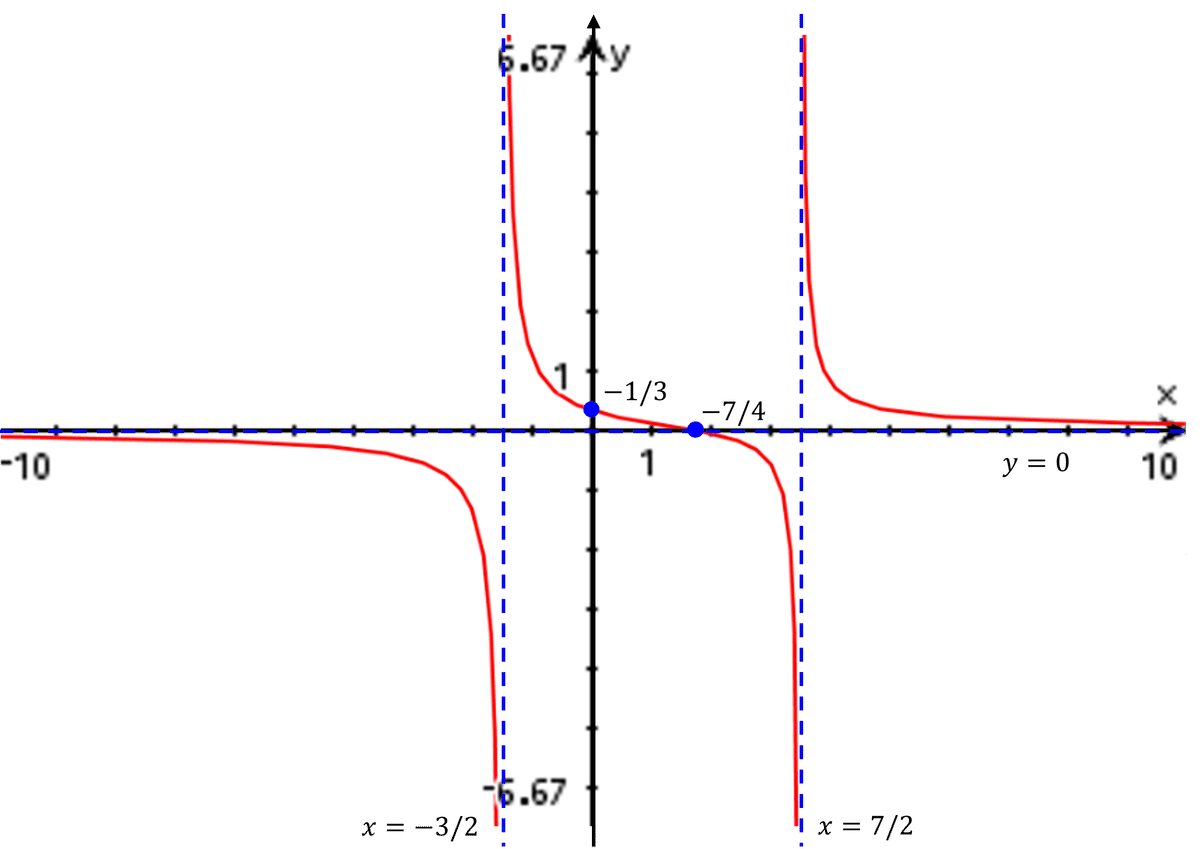
毎回 asymptotes と x-intercepts があった場合、その左右で f(x) の符号が変わらないか要チェックです。その方法としては、確認したい区間内の適当な計算しやすい数値(0 や 1 など)を代入して f(x) の値(符号が分かればOK)を求めるのが効率的です。
ちなみに、asymptotes は絶対に曲線が触れてはいけない線だと思いがちですが、今回の例のように horizontal asymptote を曲線が縦断する場合もあり得ます。あくまで、x が ∞ に近づくときに曲線が horizontal asymptote に近づくが触れない、ということを認識しておいてください。
Linear/Quadratic のルーティン
Linear/Linear に比べてやや式が複雑になってしまうため、もう一つ具体例を通してルーティンを確認しましょう。

Vertical asymptotes は 分母=0 を解いて x=0 と x=-3 だと求まります。Horizontal asymptote に関しては、実は Linear/Quadratic の場合、分母の二次式のほうが分子の一次式より増加スピードが速いため、必ず y=0 に収束します。y-intercept は f(0) の値ですが、今回の場合は分母が 0 となってしまい undefined なのでありません。x-intercept は分母が 0 とならない限り 分子=0 を解けばよいので、-4 となります。
これらの情報をx-y座標に落とし込むと、

今回の場合は x=-4 と -3 と 0 の前後での符号の変化を確認します。すると、

このようになることが分かります。あとはこれに従って曲線を描くと、

無事にグラフの出来上がりです。x=-3 と x=0 の間では f(x) は常に negative なので下から上へ向かい、再び下へ向かう曲線となることや、x=-4で一度 x-axis を縦断するものの、その後 x=-∞ にかけて y=0 に近づくことには要注意です(一瞬戸惑うかもしれませんが、言われてみれば納得ですよね)。
つまり、ルーティンとしてまとめると、Linear/Quadratic の場合は
Vertical asymptote(s), y-intercept, x-intercept を求める(horizontal asymptote は y=0)
Vertical asymptote(s) と x-intercept(s) の前後で f(x) の符号をチェック
x-y座標上に情報を書き込み、求めた条件を満たすように曲線を描く
という流れで解けばよいことになります。
Linear/Quadratic の補足
少し前に「Linear/Quadratic の場合は、基本的に vertical asymptotes は2本」と書いてあったのは覚えていますか?実際、vertical asymptote が1本しかない場合もあり、それは 分母=0 が重解となる時です(当然と言われればそうですよね)。

この例でも、vertical asymptote から左に向かっていくと、曲線が x-axis を縦断し、さらに y-intercept を通ってから、y=0 に近づいていく様子がよく分かります。
Quadratic/Linear の形の攻略法は?【HL】
Quadratic/Linear の具体例

まずは今まで同様に 分母=0 を解いて vertical asymptote が x=1 であることが分かります。ここからが他の2種類と大きく異なる点なのですが、この関数で x を無限大に飛ばすと、分子の二次式のほうが分母の一次式より速く増加するので、y も無限大に近づいて行ってしまいます。しかし、Quadratic/Linear の曲線はある直線に近づくことが知られていて、それを oblique asymptote と呼びます。
Oblique asymptote を求めるためには、式の割り算を行って 一次式 + 分数 の形にします。今回の例だと、分子/分母 = (3x+4) remainder 2 となるので、
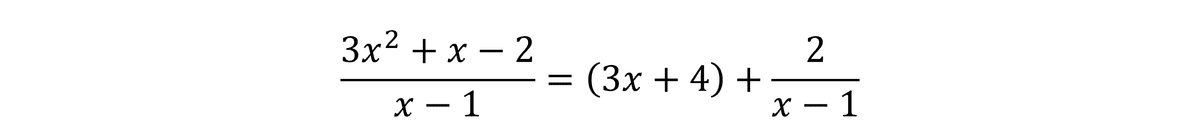
と表せます。この時、分数から取り出した一次式が oblique asymptote の直線の式となるので、この関数の oblique asymptote は y=3x+4 です。
x-intercept(s) と y-intercept の求め方は変わらないので省きますが、分子が quadratic なので x-intercept(s) が2つ出ることもあります。今までと同じようにx-y座標上に求めた情報を落とし込むと、

というようになり、これに合う曲線を描くと、

と、見事グラフの完成です。Linear/Quadratic に比べて、符号を細かく検証しなくても intercepts と asymptotes に従えばグラフが描けるので(形のパターンが基本的にこれと次に紹介するものの2種類のみ)、案外楽かもしれません。
Quadratic/Linear のルーティン
先ほどとは少し形の違う、Quadratic/Linear のグラフを描きながらルーティンの説明を行います。基本的には今までの2種類と同じ方針で進めればよいので、
Vertical asymptote, oblique asymptote(割り算), y-intercept, x-intercept(s) を求める
x-y座標上に情報を書き込み、求めた条件を満たすように曲線を描く
という流れで解けばよいことになります(符号のチェックはわざわざしなくても基本的には描けます)。例えば、

この場合は情報をx-y座標上にプロットすると

このようになり、今回は2本の asymptotes が acute angle(鋭角)を作っているほうではなく、obtuse angle(鈍角)のほうに曲線が来ることが分かります。つまり、

このようなグラフになるということです。大きく分けてこの2種類が Quadratic/Linear のグラフの形となります。どちらの場合にも、対角に曲線が2本描かれることになります。
Quadratic/Linear の補足
分子が quadratic であるがゆえに、場合によっては x-intercepts が2つあることもありますが、逆に 分子=0 が no real solution となり、x-intercept が1つもないこともあり得ます。この関数がその例です:

実際にグラフを書いてみると、

やはり曲線と x-axis が交わらないことが分かります。
ここで、少し本題からは外れて応用的な話になりますが、このグラフの local minimum/maximum を微分によって求めることができる、ということを紹介したいと思います。f'(x) = 0 となる x を求めると

したがって、x = 1 + √6 で local minimumと、x = 1 - √6 で local maximum となることが分かります。
全体のまとめ
以上で IB Math AA のシラバスに含まれる rational function は網羅しました!各種類ごとに細かい違いはあるものの、基本的な流れとしては
4点セット(vertical asymptote(s), horizontal/oblique asymptote, x-intercept(s), y-intercept)を求める
x-y座標上に情報を書き込み、必要に応じて vertical asymptote(s) と x-intercept(s) の前後で f(x) の符号をチェック
求めた条件を満たすように曲線を描く
というルーティンを踏むこと、そして
Vertical asymptotes: 分母 = 0 を解き "x=__" の形で書く
Horizontal asymptote: x を ±∞ に飛ばした時に y が収束する値(lim)
Oblique asymptote: 分子÷分母で一次式を導く
y-intercept: f(0) の値
x-intercept: f(x) = 0 となる x を求める
といった解き方を用いることは全てに共通しています。必死に解法を暗記しようとするのではなく、繰り返し練習を重ねる中で体に染み込ませていくのが効果的だと思います。
なお、asymptotes や intercepts は必ずしっかり label するようにしてください。せっかくの得点源なのに減点されてしまうと非常にもったいないです。ただし、label があったうえで最低限の概形が伝われば点数はもらえるはずなので、曲線の美しさを追求することに時間を割かずに、あくまで滑らかな線を手際よく描くことを目指してください。ちなみに、グラフは Final でも鉛筆書き可なので、いきなりペンで書き始めずに、軽く下書きをしておくことをお勧めします。
Rational function の練習には、自分で適当な関数を作り、その概形を描いたうえでGDCに入力し、答え合わせをするという方法があります。何も考えずに関数を作ってしまうと計算が悲惨なことになるかもしれませんが、基礎的な数学力やGDCを扱う力など、様々な力が伸ばせるうえ、特に textbook などが無くても取り組めるため便利です。元の関数の逆数(Quadratic/Linear が Linear/Quadratic になる、など)や inverse function(逆関数)も同じ座標にプロットしてみると、面白い発見があったりするかもしれません。ぜひ色々試してみて、rational function をマスターしてください!
リクエストを送るには?
ここまで読んでくれてありがとうございます、お疲れさまでした!
皆さんのコメントはとても励みになるので、ぜひ積極的に残していってください!
毎度のことですが、何か聞きたいことがある方はこちらの Google Form から匿名で送信いただけます。質問内容は受験やTOK/CAS/EE、IA/IO、定期テスト/Mock/Final についてでも、今回紹介したような教科の内容(「微積難しい!」など)でもOKです。皆さんが知りたい内容は積極的に記事にしていきたいと思うので、遠慮なくバンバン送っちゃってください!
