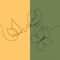フォトギャラリー用グラフ#13

13回目という事で、素数に関した不吉な画像を挙げます。極座標で、原点からの距離と偏角が共に素数になるような点をプロットすると、ヘッダ画像のような「渦」が生じるという話です。

---

この企画の目的

• 毎日投稿のバッジ獲得(365日)のため少ない労力で記事を書く

• 「みんなのフォトギャラリー」で使える数学の画像を増やす

• 理屈は抜きで、目で見て数学を楽しんで頂く

画像の説明

変数$${p}$$を1以上1万以下の素数の上を動かして、点$${(p\cos p, p\sin p)}$$をプロットしました。 

図からは奇妙な渦が見て取れますが、少なくとも渦には数学的に深い意味はありません。この点が不吉です。ただ、点がある種の均一性を持ってらせん状を散らばっていることは、ディリクレの算術級数定理と関係するらしいです。数論には詳しくないので、私が知っていることはこれだけです。

以下は、参考にしたYouTubeの動画です。

ソースコード

以下は、グラフの描画に用いたPythonのコードです。Google Collaboratory で実行しました。

import matplotlib.pyplot as plt
import numpy as np
from sympy import sieve
N = 10**5
p = np.array([i for i in sieve.primerange(2, N)])

# 極座標
x = p * np.cos(p)
y = p * np.sin(p)

r = 5.0
fig, ax = plt.subplots(figsize=(1.91*r,r))
ax.axis("off")
W = np.max(p) # x軸の表示範囲
ax.set_xlim(-W,W)
ax.set_ylim(-W/1.91, W/1.91)

ax.scatter(x,y, s = 1)
plt.show()

おまけ：1万以下の素数を使ってプロットした図