フォトギャラリー用画像#26
パスカルの三角形の二項係数を偶奇で塗り分けると現れる模様が、所謂”シェルピンスキーの ギャスケット”でした。
今回はパスカルの三角形を「2の倍数とそれ以外」、「4の倍数とそれ以外」、「8の倍数とそれ以外」、「16の倍数とそれ以外」といった規則で塗り分けた図です。



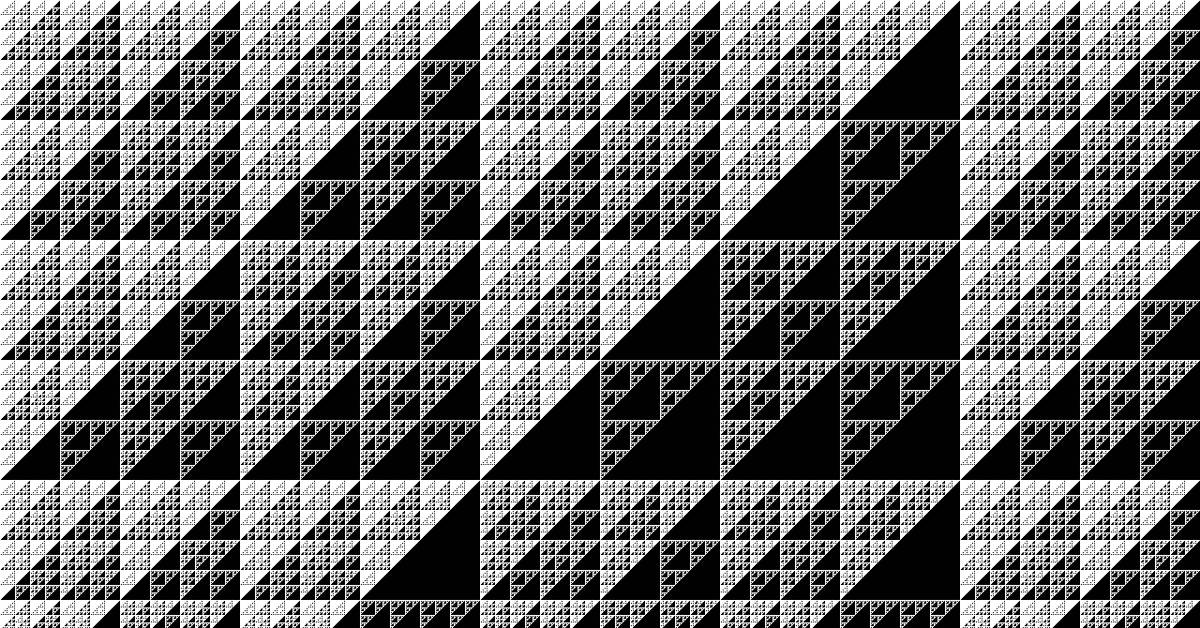


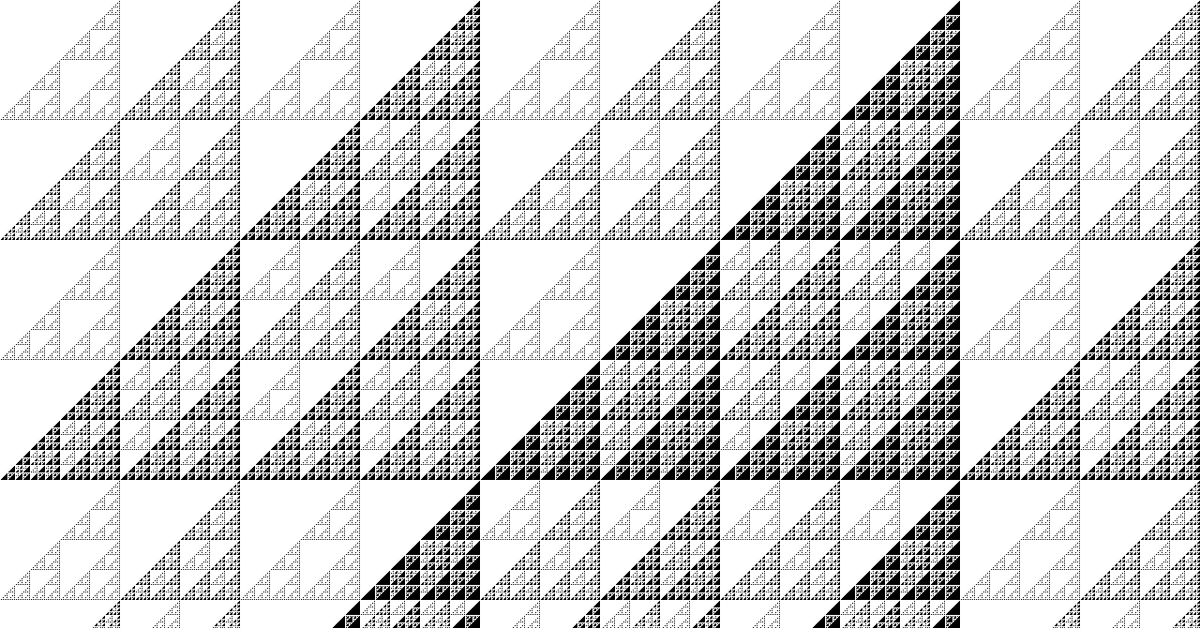

ソースコード
Google Collaboratoryの共有リンク
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
width = 1280; height = 670 # みんなのフォトギャラリー用にサイズを指定
im = np.ones((height, width))
# 二項係数をpで割った余りを計算
p = 4
h = 10 ; w = 10
mat = np.zeros((h,w))
mat[0][0]=1
for i in range (1,h):
mat[0][i] = 1
for j in range (1,i+1):
mat[j][i-j] = (mat[j-1][i-j]+mat[j][i-j-1] )%p
print(mat)
for k0 in range(8):
k = k0+1
# 二項係数をpで割った余りを計算
p = 2 ** k
n = height + width
mat = np.zeros((n,n))
mat[0][0]=1
for i in range (1,n-1):
mat[0][i] = 1
for j in range (1,i+1):
mat[j][i-j] = (mat[j-1][i-j]+mat[j][i-j-1])%p
# 余りが 0 の所は黒、それ以外は白を格納
for i in range (height):
for j in range (width):
im[i][j]= 0 if mat[i][j] == 0 else 255
#画像の表示と保存
plt.imshow(im, cmap='gray')
plt.axis('off')
plt.show()
plt.imsave('no+e_photo_gallery_026_'+str(k)+'.png', im, cmap='gray',dpi=1000 )