ラビットチャレンジレポート:ステージ3 深層学習 day2
1. 勾配消失問題
1-1 要点
■勾配消失問題
ニューラルネットワークが深くなっていくと、誤差逆伝播法が下位層に進んでいくに連れ微分値が掛け合わされていき、勾配が0に近づいていく。こうなるとパラメータはほとんど更新されず、訓練が最適値に収束しなくなってしまう。
活性化関数にシグモイド関数を用いた場合を考えると、$${f'(u)=f(u)(1-f(u))}$$であり、最大値は0.25である。このような小さな値が掛けられていくと、上記の勾配消失問題を引き起こすことが予想できる。
■勾配消失問題の解決方法
◆活性化関数の選択
ReLU関数を用いる。
ReLU関数の微分値は、$${u\leqq0}$$では$${0}$$、$${u>0}$$では$${1}$$のため、勾配消失問題を回避することができる。
◆重み初期値の設定方法
・Xavierの初期化
活性化関数としてシグモイド関数、ReLU、双曲線正接関数を用いている場合に使用する。
重みの要素を、前の層のノード数の平方根で除算した値とする。
重みを標準正規分布で初期化した場合、シグモイド関数を通った各レイヤーの出力は0または1に偏る。また、標準偏差を小さくした分布から重みを生成した場合(0付近に偏った値が出力される)各レイヤーの出力は0.5付近に偏る。
Xavierの初期化を行った場合、各レイヤーの出力は0.5を頂点とした釣鐘状の形状になる。これにより、表現力のあるモデルを得ることができるようになる。
・Heの初期化
活性化関数としてReLU関数を用いている場合に使用する。
重みの要素を、の層のノード数の平方根で除算した値に$${\sqrt2}$$を掛けた値とする
重みを標準正規分布で初期化した場合、ReLU関数を通った各レイヤーの出力は0に偏る。また、標準偏差を小さくした分布から重みを生成した場合も各レイヤーの出力は0付近に偏る。
Heの初期化を行った場合、各レイヤーの出力は0付近を頂点とした釣鐘状の形状になる。これにより、表現力のあるモデルを得ることができるようになる。
◆バッチ正規化
ミニバッチ単位で入力値のデータの偏りを抑制する手法。
学習データを正規化することで極端なばらつきを抑えることができる。
(下式)


1-2 実装演習
ministデータ分類の学習を、活性化関数にシグモイド関数を使った場合と、ReLU関数を使った場合で比較した。
import numpy as np
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 重み初期値補正係数
wieght_init = 0.01
# 入力層サイズ
input_layer_size = 784
# 中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
# 出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval = 10
# 初期設定
def init_network():
network = {}
network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_f = functions.sigmoid
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_d_f = functions.d_sigmoid
last_d_f = functions.d_softmax_with_loss
# 出力層でのデルタ
delta3 = last_d_f(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1: d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i + 1) % plot_interval == 0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()結果、2000エポック分学習を行ったが、正答率は全く向上しなかった。

Generation: 2000. 正答率(トレーニング) = 0.06
: 2000. 正答率(テスト) = 0.1028次に、活性化関数をReLUに変えた。
import numpy as np
from data.mnist import load_mnist
from common import functions
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 重み初期値補正係数
wieght_init = 0.01
# 入力層サイズ
input_layer_size = 784
# 中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
# 出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval = 10
# 初期設定
def init_network():
network = {}
network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ##############
hidden_f = functions.relu
#################################
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ##############
hidden_d_f = functions.d_relu
#################################
# 出力層でのデルタ
delta3 = functions.d_softmax_with_loss(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1: d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i + 1) % plot_interval == 0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()学習が進むにつれ、訓練データ、テストデータともに正答率の向上が見られた。

Generation: 2000. 正答率(トレーニング) = 0.89
: 2000. 正答率(テスト) = 0.9159次に、活性化関数をシグモイド関数、重みの初期化にXavierの初期値を使用した場合を見る。
import numpy as np
from data.mnist import load_mnist
from common import functions
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 入力層サイズ
input_layer_size = 784
# 中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
# 出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval = 10
# 初期設定
def init_network():
network = {}
########### 変更箇所 ##############
# Xavierの初期値
network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / (np.sqrt(input_layer_size))
network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / (np.sqrt(hidden_layer_1_size))
network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / (np.sqrt(hidden_layer_2_size))
#################################
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_f = functions.sigmoid
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_d_f = functions.d_sigmoid
# 出力層でのデルタ
delta3 = functions.d_softmax_with_loss(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1: d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i + 1) % plot_interval == 0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()正しく学習が進み、正答率が改善されていることが分かる。

Generation: 2000. 正答率(トレーニング) = 0.83
: 2000. 正答率(テスト) = 0.82451-3 確認テスト
◆確認テスト①

回答①

◆確認テスト②

回答②

◆確認テスト③

回答③
すべての重みの値が均一に更新されるため、多数の重みを持つ意味がなくなり、正しい学習が行えなくなってしまう。
◆確認テスト④

回答④
・中間層の学習が安定する。
・過学習を抑えることができる。
◆確認テスト⑤

回答⑤
(1) data_x[i:i_end], data_t[i:i_end]
2. 学習率最適化手法
2-1 要点
■学習率
重み更新の際に、誤差を重みで微分した値に掛けられる係数。
学習率が大きすぎる場合、誤差がいつまでも最小値にたどり着かず発散してしまう。
学習率が小さすぎる場合、収束するまでに時間がかかってしまう。
従って、学習率設定方法の指針が必要になる。
・初期の学習率を大きく設定し、徐々に学習率を小さくしていく。
・パラメータごとに学習率を可変させる。
この指針に従い、以下のような様々な学習率最適化手法が考案されている。
■Momentum
誤差をパラメータで微分した元学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算するして重みを更新する。
$${V}$$は前回の重み。$${\mu}$$は慣性(ハイパーパラメータ)

メリット
・局所最適解にはならず、大域的最適解となる。
・谷間についてから最も低い位置に行くまでの時間が短い。
■AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算して重みを更新する。$${h}$$にはそれまでの学習の過程が蓄積されており、学習率決定に利用する。

メリット
・勾配の緩やかな斜面に対して、最適地に近づける。
課題
・学習率が徐々に小さくなるので鞍点問題を引き起こすことがある。
■RMSProp
誤差をパラメータで微分したものと再定義した学習率の積を減算して重みを更新する。

メリット
・局所最適解にはならず、大域的最適解となる。
・ハイパーパラメータの調整が必要な場合が少ない。
■Adam
Momentumの過去の勾配の指数関数的減衰平均と、RMSPropの過去の勾配の二乗の指数関数的減衰平均、それぞれを孕んだ最適化アルゴリズムであり、両者のメリットを持った最適化手法である。
2-2 実装演習
最適化手法を、SGD、Momentum、Adamに変更し、結果の比較を行った。
①SGD
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid',
weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()全く学習が上手くいっていない。

②Momentum
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid',
weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.3
# 慣性
momentum = 0.9
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
v = {}
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
v[key] = np.zeros_like(network.params[key])
v[key] = momentum * v[key] - learning_rate * grad[key]
network.params[key] += v[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()SGDよりもかなり改善している。

Generation: 1000. 正答率(トレーニング) = 0.92
: 1000. 正答率(テスト) = 0.9315③Adam
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid',
weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
m = {}
v = {}
learning_rate_t = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()Momentumよりもさらに正答率が改善し、収束も早かった。

Generation: 1000. 正答率(トレーニング) = 0.98
: 1000. 正答率(テスト) = 0.94912-3 確認テスト
◆確認テスト①

回答①
・Momentum
局所最適解にはならず、大域的最適解となる。
谷間についてから最も低い位置に行くまでの時間が短い。
・AdaGrad
勾配の緩やかな斜面に対して、最適地に近づける。
学習率が徐々に小さくなるので鞍点問題を引き起こすことがある。
・RMSProp
局所最適解にはならず、大域的最適解となる。
ハイパーパラメータの調整が必要な場合が少ない。
3. 過学習
3-1 要点
■過学習とは
訓練データに過剰に適合しすぎてモデルの汎化性能が低下した状態。訓練データとの誤差は小さくなるが、テストデータとの誤差は大きくなる。

■原因
・パラメータの数が多い
・パラメータの値が適切でない
・ノードが多い etc…
まとめて言うと、ネットワークの自由度が高い(高すぎる)状態。
■対策
・L1正則化(ラッソ回帰)
・L2正則化(リッジ回帰)
・ドロップアウト
■L1正則化、L2正則化
過学習の原因として、重みが大きい値を取ることで過学習が発生することがある。
よって、解決策としては、誤差に対して正則化項を加算することで重みが大きくなりすぎるのを抑制することができる。
・正則化の計算
誤差関数にpノルムを加える。

pノルムは以下。

p = 1の場合をL1正則化、p = 2の場合をL2正則化と呼ぶ。
pノルムの具体的な計算は以下のようになる。
$$(\lambda)$$は正則化率と呼ばれるハイパーパラメータ。

■ドロップアウト
ランダムにノードを削除して学習させることで、自由度を抑えたモデルを作る手法。データ量を変化させることなく、異なるモデルを学習させている(アンサンブル学習)と解釈できる。
3-2 実装演習
正則化、ドロップアウトの効果を以下のコードで確かめた。
まず、過学習対策なしの場合。
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:200]
d_train = d_train[:200]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
訓練データは精度1.0となったが、テストデータは最終的に0.7程度であった。
次に、L2正則化。
正則化係数$${\lambda}$$の値を0.001~1まで変更して比較した。
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:200]
d_train = d_train[:200]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.0001
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num + 1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params[
'W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title(f"accuracy(λ = {weight_decay_lambda})")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

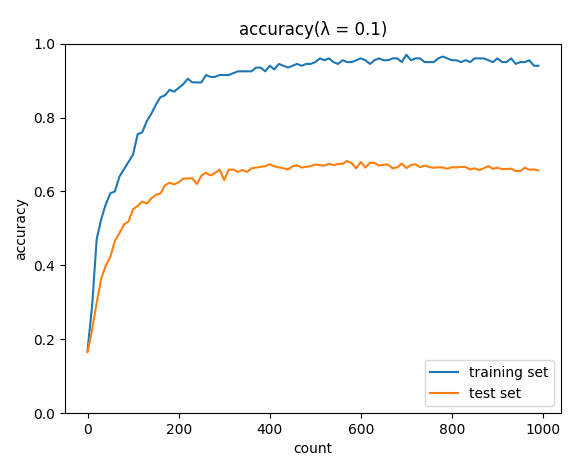

正則化係数0.001では正則化なしの時と変わらず、0.01でテストデータの正解率0.73とわずかに改善が見られた。0.1、1.0ではかえって学習が上手くいかなかった。正則化係数が小さすぎる場合、重みの最適解は対策なしの時とほとんど変わらず、正則化係数が大きすぎる時はほとんどの重みが0に近い値になっているのではないかと思われる。
見てみると以下のようになっていた。
print(f"λ={weight_decay_lambda}")
print(network.params)λ=1.0
{'W1': array([[-2.40223786e-07, 1.02989594e-06, 1.05564354e-06, ...,
-2.57750346e-06, 1.47779211e-07, 4.30858473e-08],
[-2.33172114e-06, 8.66593922e-07, -3.87402461e-07, ...,
-2.58511685e-06, 5.94247939e-07, 3.45138584e-06],
[ 6.94723746e-07, 2.74259918e-06, 3.09758756e-06, ...,
λ=0.01
{'W1': array([[ 0.04264706, -0.01284167, 0.00805445, ..., -0.00175541,
-0.05484134, -0.04428674],
[-0.00791543, -0.01378973, 0.0663816 , ..., -0.03987108,
0.08252611, 0.0017771 ],
[ 0.02661368, 0.02044808, -0.01868208, ..., -0.03150986,
-0.0131748 , -0.00317399],
...,次にL1正則化。
正則化係数を0.00005~0.05まで変化させて結果を比較した。
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.00005
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num + 1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(
network.params['W' + str(idx)])
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title(f"accuracy(λ = {weight_decay_lambda})")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
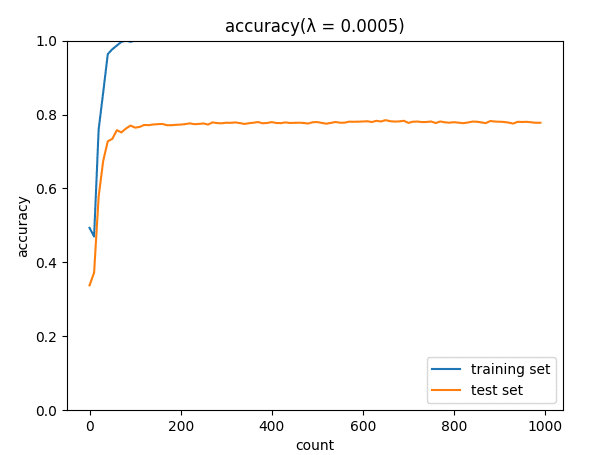


正則化係数0.00005でテストデータに対する正解率0.78と、この時に最も良い結果だった。
次にドロップアウトを試した。
ドロップアウト率を0.05、0.15、0.3と変化させた。
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:200]
d_train = d_train[:200]
# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.05
weight_decay_lambda = 0.00005
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda, use_dropout=use_dropout, dropout_ratio=dropout_ratio)
optimizer = optimizer.SGD(learning_rate=0.01)
# optimizer = optimizer.Momentum(learning_rate=0.01, momentum=0.9)
# optimizer = optimizer.AdaGrad(learning_rate=0.01)
# optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title(f"accuracy(ratio:{dropout_ratio})")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()


ドロップアウト率0.05でテストデータに対する正解率0.78と、この時が最も良い結果だった。
3-3 確認テスト
◆確認テスト①

回答①
右がL1正則化。
ベクトルで考えた場合、L1ノルムはマンハッタン距離、L2ノルムはユークリッド距離を意味するので図形的に右がL1正則化になると解釈した。
ただし、誤差関数は重み行列の関数になっていて、誤差関数に足されているのも行列のノルムなので、本当にこの例えの通りの解釈ができるかは現在理解できていない。追加で調べる必要があると感じている。
◆確認テスト②

回答②
(4)param
L2ノルムは||param||^2になるので、その勾配が誤差の勾配に加えられる。
計算上は微分になるので、2*paramとなるが、正則化項の1/2と相殺されparamが答えになる。
◆確認テスト③

回答③
(3)np.sign(param)
計算上は|param|の微分値が誤差の勾配に加えられる。
下図のようになるため、答えは符号関数を使用したnp.sign(param)になると考えられる。

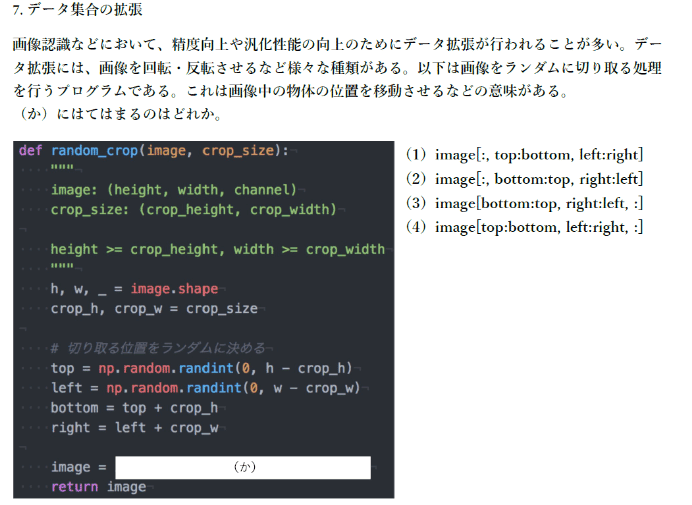
◆確認テスト④
回答④
(4)image[top:bottom, left:right]
リストのスライスと同じような表記で、縦の切り抜き開始index、縦の終了index、横の開始index、横の終了indexを使っている。
4. 畳み込みニューラルネットワークの概念
4-1 要点
■畳み込みニューラルネットワーク(CNN)とは
入力データに対して、「畳み込み層」と「プーリング層」による変換処理を行い、データの特徴を捉える手法。このような処理を行うことで、例えば画像データ等、あるデータ点と周囲のデータ点に関連性がある場合等、その関連性を保ったまま学習を行うことができる。
構造の一例と、CNNを使用した代表的なネットワークの一つ、LeNetの構造を以下に示す。

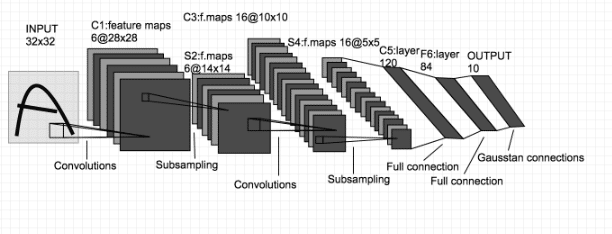
これらの例では、畳み込み層とプーリング層を通した後、全結合層によって画像の分類結果を出力している。
■畳み込み層
畳み込み層においては、入力データに対してフィルターによる処理を施し、新たなデータを得る。具体的な計算例は以下のようになる。4×4の入力画像の赤四角の部分に対して、3×3のフィルターによる処理が行われ、処理後の値が新たな出力データの赤四角の部分に入る場合を示している。
計算においては入力データとフィルターの重なった部分の数値を掛け合わせ、全てを足し合わせたもの(ここでは141)が最終の結果になる。

この処理を、フィルターの位置をずらしながら行い、出力データの値が得られる。

この時、出力データの解像度は入力データよりも低くなるが、これを抑えるために入力画像の周囲に値を入れる場合がある。これをパディングと言う。
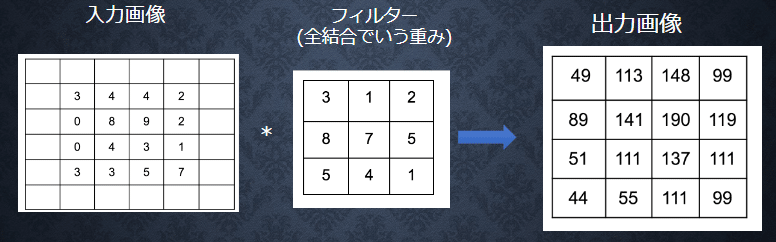
また、処理ごとのフィルター位置の移動量をストライドと言う。
(これまでの例はストライド1)
■プーリング層
入力データのある範囲内で最大値または平均値を取る操作を繰り返し行い、これらを新しい出力データとする。
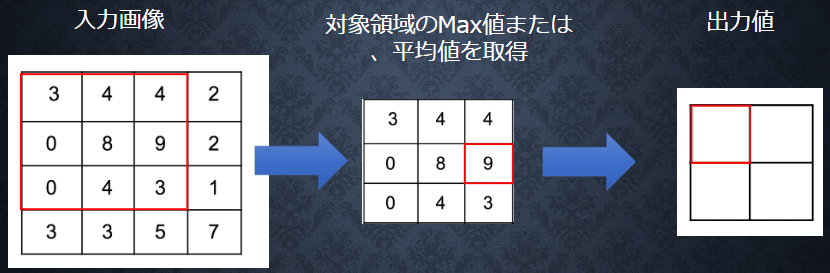
4-2 実装演習
画像データを2次元配列に変換する関数の動作を確認。
import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# 画像データを2次元配列に変換
'''
input_data: 入力値
filter_h: フィルターの高さ
filter_w: フィルターの横幅
stride: ストライド
pad: パディング
'''
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_data.shape
# 切り捨て除算
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3) # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)
col = col.reshape(N * out_h * out_w, -1)
return col
# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')#出力結果
========== input_data ===========
[[[[48. 51. 47. 67.]
[48. 98. 40. 7.]
[12. 80. 38. 86.]
[ 4. 98. 3. 1.]]]
[[[60. 46. 80. 74.]
[83. 66. 64. 33.]
[51. 45. 7. 60.]
[65. 86. 13. 48.]]]]
==============================
============= col ==============
[[48. 51. 47. 48. 98. 40. 12. 80. 38.]
[51. 47. 67. 98. 40. 7. 80. 38. 86.]
[48. 98. 40. 12. 80. 38. 4. 98. 3.]
[98. 40. 7. 80. 38. 86. 98. 3. 1.]
[60. 46. 80. 83. 66. 64. 51. 45. 7.]
[46. 80. 74. 66. 64. 33. 45. 7. 60.]
[83. 66. 64. 51. 45. 7. 65. 86. 13.]
[66. 64. 33. 45. 7. 60. 86. 13. 48.]]
==============================処理としては、まず画像データからフィルタの動く範囲の数(横×縦)の配列をフィルタの要素数分の個数作り、tranposeで同じ位置の数値(例えば、配列[0, 0]の数値)をフィルタの要素数分集めて再構成(軸の変更)し、最後にreshapeで2次元の配列に変換している。
次に、配列データを画像データに変換する関数の動作を確認した。
img = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print#結果
[[[[ 48. 102. 94. 67.]
[ 96. 392. 160. 14.]
[ 24. 320. 152. 172.]
[ 4. 196. 6. 1.]]]
[[[ 60. 92. 160. 74.]
[166. 264. 256. 66.]
[102. 180. 28. 120.]
[ 65. 172. 26. 48.]]]]4-3 確認テスト
◆確認テスト①

回答①
7×7
パディング1を入れるため、8×8の画像を2×2のフィルタで畳み込むことになる。ストライド1の場合、フィルタの左上のマスは8×8画像の座標(7, 7)まで動く(1始まりで考えている)。よって7×7の画像に畳み込まれる。
5. 最新のCNN
5-1 要点
AlexNetは、2012年のILSVRC 2012で優勝した画像認識モデルである。構造は以下のようになっている。

5層の畳み込み層、プーリング層を通った後、データはFlatten処理され全結合層に渡される。全結合層では過学習対策のためにドロップアウトが用いられている。
5-2 実装演習
comvolution class, pooling class, simplecomvolution network classと、これらを使ったCNNでの、mnistのデータの分類の動作を確認した。
import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# 画像データを2次元配列に変換
'''
input_data: 入力値
filter_h: フィルターの高さ
filter_w: フィルターの横幅
stride: ストライド
pad: パディング
'''
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_data.shape
# 切り捨て除算
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
print(col)
col = col.transpose(0, 4, 5, 1, 2, 3) # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)
col = col.reshape(N * out_h * out_w, -1)
return col
# 2次元配列を画像データに変換
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_shape
# 切り捨て除算
out_h = (H + 2 * pad - filter_h)//stride + 1
out_w = (W + 2 * pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2) # (N, filter_h, filter_w, out_h, out_w, C)
img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
class Convolution:
# W: フィルター, b: バイアス
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# フィルター・バイアスパラメータの勾配
self.dW = None
self.db = None
def forward(self, x):
# FN: filter_number, C: channel, FH: filter_height, FW: filter_width
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
# 出力値のheight, width
out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
# xを行列に変換
col = im2col(x, FH, FW, self.stride, self.pad)
# フィルターをxに合わせた行列に変換
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
# 計算のために変えた形式を戻す
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
# dcolを画像データに変換
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# xを行列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# プーリングのサイズに合わせてリサイズ
col = col.reshape(-1, self.pool_h * self.pool_w)
# maxプーリング
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
class SimpleConvNet:
# conv - relu - pool - affine - relu - affine - softmax
def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'],
conv_param['pad'])
self.layers['Relu1'] = layers.Relu()
self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = layers.Relu()
self.layers['Affine2'] = layers.Affine(self.params['W3'], self.params['b3'])
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x):
for key in self.layers.keys():
x = self.layers[key].forward(x)
return x
def loss(self, x, d):
y = self.predict(x)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1: d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i * batch_size:(i + 1) * batch_size]
td = d[i * batch_size:(i + 1) * batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grad = {}
grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grad['W2'], grad['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grad['W3'], grad['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grad
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
print("データ読み込み完了")
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[:5000], d_train[:5000]
x_test, d_test = x_test[:1000], d_test[:1000]
network = SimpleConvNet(input_dim=(1, 28, 28), conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval = 10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i + 1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i + 1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()結果

#結果
Generation: 1000. 正答率(トレーニング) = 0.992
: 1000. 正答率(テスト) = 0.9612-2で行ったAdamを使用した場合の、全結合型ニューラルネットワークの結果よりも良い正解率だった。
学習には自宅のパソコンで10分以上を要した。これまで実装演習で行ったどのネットワークよりも大幅に長い時間が必要な手法であると分かった。
5-3 確認テスト
◆確認テスト①

回答①
3×3
パディング1を入れるため、7×7の画像を3×3のフィルタで畳み込むことになる。ストライド2の場合、フィルタの左上のマスは7×7画像の座標(5, 5)まで、座標を1つ飛ばしで動く(1始まりで考えている)。よって3×3の画像に畳み込まれる。
