ラビットチャレンジレポート:ステージ3 深層学習 day1
ニューラルネットワークの全体像は下図のようになっており、それぞれの部分ごとにレポートをまとめていく。
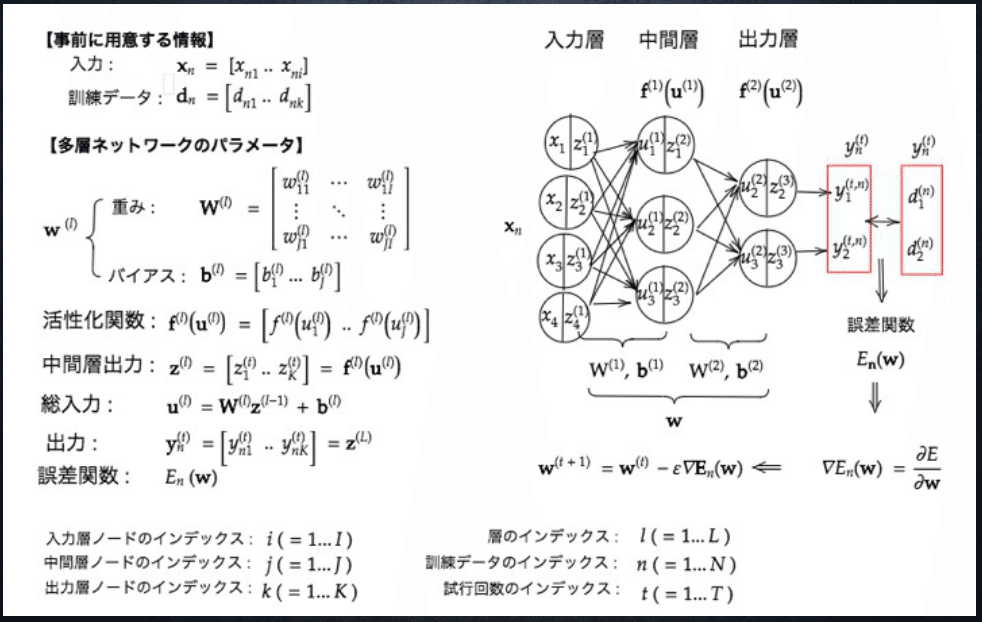
1. 入力層~中間層
1-1 要点
■入力層
処理するべきデータを数値として受け取る層。
受け取った値は重みを掛け合わされた後、バイアス項とともに足し合わされ、中間層の各ノードに渡される。
数式上は
$$
\begin{align*}
u&=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b\\
&=\bm{W}\bm{x}+b
\end{align*}
$$
のように表される。
■中間層
入力層から受け取った値を活性化関数に通し、次の層へ出力する働きを持つ。中間層が多層の場合、この値は次の層への入力として使用される。
数式上は
$$
z=f(u)
$$
のように表される。
1-2 実装演習
必要なライブラリをインポート。
このレポートではコードの実行のpycharm2021.2.2を使用し、配布のcommonファイルはライブラリフォルダに格納した。
順伝播(単層・単ユニット)
import numpy as np
from common import functions
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
#print("shape: " + str(x.shape))
print("")
x = [1,2,3]
print_vec("test",x) #実際に動くかテスト#出力結果
*** test ***
[1, 2, 3]重みの初期化
W = np.array([[0,1],[0,2]])
print_vec("重み",W)
#試してみよう配列の初期化
W = np.zeros(2)
print_vec("ゼロベクトル",W)
W = np.ones(2)
print_vec("要素全部1",W)
W = np.random.rand(2)
print_vec("ランダム(0~1)",W)
W = np.random.randint(5, size=(2))
print_vec("ランダム(1~4整数)",W)#出力結果
*** 重み ***
[[0 1]
[0 2]]
*** ゼロベクトル ***
[0. 0.]
*** 要素全部1 ***
[1. 1.]
*** ランダム(0~1) ***
[0.90495197 0.26646005]
*** ランダム(1~4整数) ***
[0 2]バイアスの初期化
# バイアス
b = 0.5
print_vec("バイアス", b)
# 試してみよう_数値の初期化
b = np.random.rand() # 0~1のランダム数値
print_vec("ランダム(0~1)", b)
b = np.random.rand() * 10 -5 # -5~5のランダム数値
print_vec("ランダム(-5~5)", b)*** バイアス ***
0.5
*** ランダム(0~1) ***
0.1434225120214645
*** ランダム(-5~5) ***
4.578974716405892入力、総出力、中間層出力
# 入力値
x = np.array([2, 3])
print_vec("入力", x)
# 総入力
u = np.dot(x, W) + b
print_vec("総入力", u)
# 中間層出力
z = functions.relu(u)
print_vec("中間層出力", z)#出力結果
*** 入力 ***
[2 3]
*** 総入力 ***
4.566407166972704
*** 中間層出力 ***
4.5664071669727041-3 確認テスト
◆確認テスト①

回答①
多数の中間層を持つニューラルネットワークを用いて、入力値から目的とする出力値に変換する数学モデルを構築することを目的としている。
・選択肢
③重み、④バイアス
◆確認テスト②

回答②

◆確認テスト③
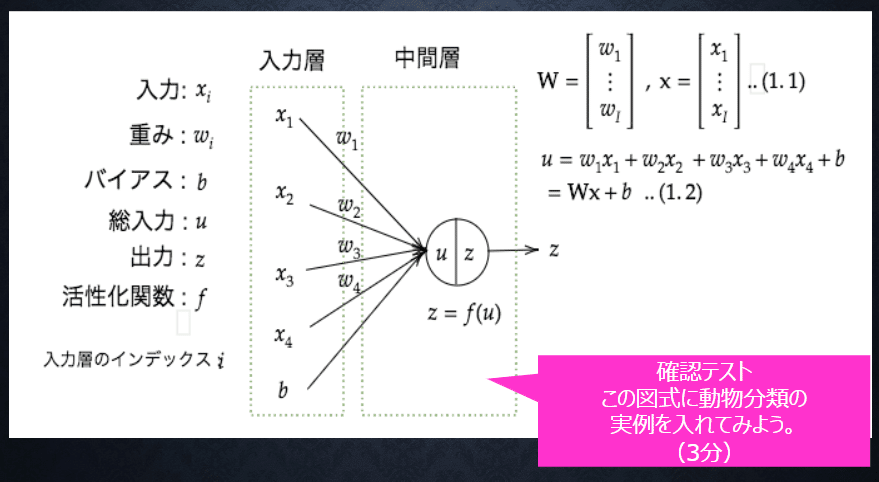
回答③

◆確認テスト④

回答④
u = W.dot(x)+b◆確認テスト⑤
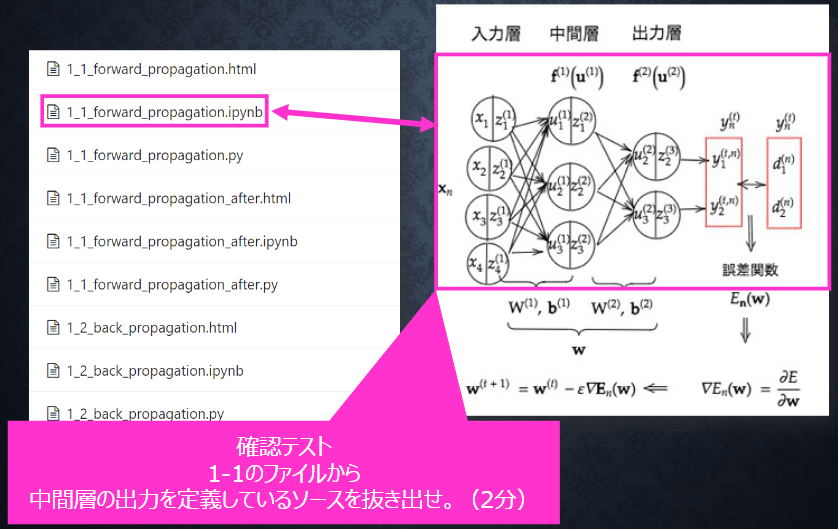
回答⑤
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)1-1のファイル内の順伝播(3層・複数ユニット)から抜き出した。
このコードでは入力が重みW1とバイアスb1で処理された後1つ目の中間層(1層目)に入り、活性化関数を通った後、次の層へ出力される。これが重みW2とバイアスb2で処理された後、2つ目の中間層(2層目)に入り、活性化関数を通った後、出力層に出力される。中間層は1、2層目にあたるので、1、2層の総出力部分を抜き出した。
2. 活性化関数
2-1 要点
ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数。入力値の値によって、次の層への信号のON・OFFや強弱を定める働きを持つ。
中間層と出力層では異なる活性化関数が用いられる。
代表的なものとしては以下。
■中間層用の活性化関数
・シグモイド関数
$$
f(u)=\frac 1 {1+e^{-u}}
$$

実数値を0~1の値に変換する関数。
入力信号の強弱を伝えることができ、ニューラルネットワーク普及のきっかけになった。
しかし、微分値の最大値が0.25と小さく、勾配消失問題を引き起こすことがある。
・ReLU関数
$$
f(u)=\begin{cases}x (x>0)\\ 0 (x\leqq 0)\end{cases}
$$

最も使われることの多い活性化関数。
勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
■中間層用の活性化関数
・恒等写像
$$
f(u)=u
$$
回帰問題において用いられる。
・シグモイド関数、ソフトマックス関数
$$
f(u)=\frac 1 {1+e^{-u}}\\
\\
f(i,u)=\frac {e^{u_i}} {\textstyle\sum_{k = 1}^K e^{u_k}}
$$
シグモイド関数は二値分類で、ソフトマックス関数は多クラス分類で用いられる。
2-2 実装演習
3層・複数ユニットでネットワークを作成する関数と、順伝播・出力までの処理を行う関数を定義。
# ネットワークを作成
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
network['W1'] = np.random.rand(2,3)
network['W2'] = np.random.rand(3,2)
network['W3'] = np.random.rand(2,2)
network['b1'] = np.random.rand(3)
network['b2'] = np.random.rand(2)
network['b3'] = np.random.rand(2)
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("重み3", network['W3'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
print_vec("バイアス3", network['b3'])
return network
# 順伝播
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
# 1層の総入力
u1 = np.dot(x, W1) + b1
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 2層の総出力
z2 = functions.relu(u2)
# 出力層の総入力
u3 = np.dot(z2, W3) + b3
# 出力層の総出力
y = u3
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力1", z1)
print("出力合計: " + str(np.sum(z1)))
return y, z1, z2
# 入力値
x = np.array([1., 2.])
print_vec("入力", x)
# ネットワークの初期化
network = init_network()
y, z1, z2 = forward(network, x)
print(y)
print(z1)
print(z2)#出力結果
*** 入力 ***
[1. 2.]
##### ネットワークの初期化 #####
*** 重み1 ***
[[0.50385228 0.13562592 0.47551037]
[0.85115872 0.29639814 0.70410728]]
*** 重み2 ***
[[0.51956432 0.69071879]
[0.57602655 0.60448675]
[0.02956807 0.88433468]]
*** 重み3 ***
[[0.75027774 0.90088777]
[0.69648042 0.03922487]]
*** バイアス1 ***
[0.84695848 0.80682443 0.26777591]
*** バイアス2 ***
[0.05405055 0.26614599]
*** バイアス3 ***
[0.25665376 0.55467933]
##### 順伝播開始 #####
*** 総入力1 ***
[3.0531282 1.53524662 2.15150083]
*** 中間層出力1 ***
[3.0531282 1.53524662 2.15150083]
*** 総入力2 ***
[2.58830557 5.20568204]
*** 出力1 ***
[3.0531282 1.53524662 2.15150083]
出力合計: 6.739875647515937
[5.82425743 3.09064435]
[3.0531282 1.53524662 2.15150083]
[2.58830557 5.20568204]2-3 確認テスト
◆確認テスト①

回答①

線型な関数は、加法性($${f(x+y)=f(x)+f(y)}$$)、斉次性($${f(kx)=kf(x)}$$)を満たすが、非線型関数はこれらを満たさない。
◆確認テスト②

回答
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)1-1のファイル内の順伝播(3層・複数ユニット)から抜き出した。
このコードでは、1つ目の中間層と2つ目の中間層で活性化関数としてReLU関数を使用している。
3. 出力層
3-1 要点
■出力層の役割
中間層までで計算された値を、我々が欲しい形に変換する。
回帰問題であれば、入力された説明変数から得られる目的変数の予測値。
分類問題であれば、各クラスと分類される確率。
■誤差関数
出力された予測値や確率の、訓練データからのずれの大きさを表す関数。
回帰問題では二乗誤差、分類問題では交差エントロピー誤差等が使用される。
$$
\begin{align*}
E_n(W)&=\frac1 2 \displaystyle\sum_{i=1}^I (y_n-d_n)^2 二乗誤差\\
E_n(W)&=-\displaystyle\sum_{i=1}^I d_i\log y_i 交差エントロピー
\end{align*}
$$
■活性化関数
回帰問題では恒等写像、分類問題ではシグモイド関数(二値分類)、ソフトマックス関数(多クラス分類)が用いられる。
3-2 実装演習
平均二乗誤差関数、クロスエントロピー関数を定義し、いくつかの値で動作を確かめた。
# 平均二乗誤差
def mean_squared_error(d, y):
return np.mean(np.square(d - y)) / 2
print("*******平均二乗誤差*******")
d = np.array([1,2,3,4,5])
y = np.array([1,2,3,4,5])
MSE1 = mean_squared_error(d,y)
print(MSE1)
y = np.array([0,0,0,0,0])
MSE2 = mean_squared_error(d,y)
print(MSE2)
y = np.array([-1,-2,4,4,3])
MSE3 = mean_squared_error(d,y)
print(MSE3)
# クロスエントロピー
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
print("*******クロスエントロピー誤差*******")
#正解ラベルや、yの予測値の組み合わせを変化
d = np.array([0])
y = np.array([0.2,0.8])
CE1 = cross_entropy_error(d,y)
print(CE1)
d = np.array([0])
y = np.array([0.02,0.98])
CE2 = cross_entropy_error(d,y)
print(CE2)
d = np.array([1])
y = np.array([0.02,0.98])
CE3 = cross_entropy_error(d,y)
print(CE3)
#バッチサイズ2
d = np.array([1,0])
y = np.array([[0.02,0.98],[0.9,0.1]])
CE4 = cross_entropy_error(d,y)
print(CE4)
d = np.array([1,1])
y = np.array([[0.02,0.98],[0.9,0.1]])
CE5 = cross_entropy_error(d,y)
print(CE5)
#dがone-hot-vector
d = np.array([[0,1],[0,1]])
y = np.array([[0.02,0.98],[0.9,0.1]])
CE6 = cross_entropy_error(d,y)
print(CE6)#出力結果
*******平均二乗誤差*******
0.0
5.5
2.5
*******クロスエントロピー誤差*******
1.6094374124342252
3.912018005440646
0.0202026052767084
0.0627815049117149
1.1613933491356272
1.16139334913562723-3 確認テスト
◆確認テスト①

回答①
・誤差の合計の大きさを評価に用いたいため、誤差を足し合わせた時に正負で打ち消し合わないように2乗している。
・この後、ネットワークの学習時に行う誤差逆伝播法の計算で誤差関数の微分を用いるが、微分後の式で係数2が出てくるので、これを打ち消すために1/2をかけてある。誤差関数は学習前と後での大小関係だけが問題になるため、計算を簡単にする目的があるだけで本質的な意味は無い。
◆確認テスト②

回答②
①softmax(x)のi番目の要素が$${f(i,u)}$$に該当する。
②np.exp(x)
③np.sum(np.exp(x))
一行ごとの処理は以下のコメントに記入した。
def softmax(x): #関数定義
if x.ndim == 2: #ミニバッチまたはバッチ学習の場合このif文が実行される
x = x.T #xを転置
x = x - np.max(x, axis=0) #オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) #入力データごと、要素ごとに確率値を求める
return y.T #yを転置してリターン
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x)) #要素ごとの確率値を求めてそのベクトルを返す・ミニバッチまたはバッチ学習の時、xはベクトルの集まり(行列)になるのでx.ndimは2になる。if文ではこれを判定している。
・オーバーフロー対策で要素の中の最大値を全要素から引いているが、$${\frac {e^{u_i-m}} {\textstyle\sum_{k=1}^Ke^{u_k-m}}=\frac {e^{-m}・e^{u_i}} {\textstyle\sum_{k=1}^Ke^{-m}・e^{u_k}}=\frac {e^{u_i}} {\textstyle\sum_{k=1}^Ke^{u_k}}}$$となるため計算結果は同じになる。この処理を行うと逆に0として扱われる要素も出てくると思われるが、オーバーフローを起こすほど大きな値が存在する状況では元々相対的に確率は0と変わらないので問題ないということだろう。
◆確認テスト③
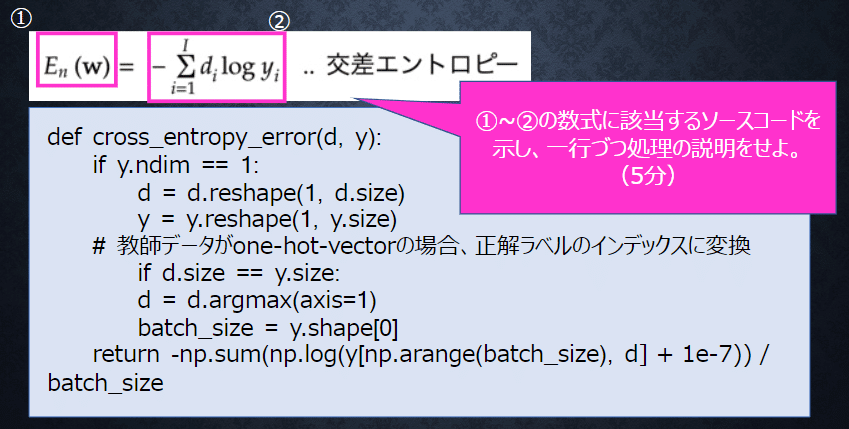
回答③
①cross_entropy_error(d, y)
②-np.sum(np.log(y[np.arange(batch_size), d] + 1e-7))
一行ごとの処理は以下のコメントに記入した。
def cross_entropy_error(d, y): #関数定義
if y.ndim == 1: #オンライン学習であるかどうかを判定
d = d.reshape(1, d.size) #オンライン学習であればreshape
y = y.reshape(1, y.size) ⇒ バッチサイズ1のミニバッチ学習をしているのと同じ配列形状になる
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size: #One-hotベクトルであればdとyの形状は同じになる(dはyのデータ数×各データの要素数の形状)
d = d.argmax(axis=1) #d = 1になっているindex(これが正解ラベル)を集めたベクトルに再構成
batch_size = y.shape[0] #バッチサイズを取得
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
#yの各データからindex = dの要素のみ対数を取って合計し、最後にマイナスをつける。
#1e-7を足すのはlogの中身が0になるのを防ぐため。
#最後にバッチサイズで割り、バッチ内での平均誤差を出している。4. 勾配降下法
4-1 要点
深層学習の学習とは、誤差関数$${E(w)}$$を最小にするパラメータ$${w}$$を発見すること。
勾配降下法とは、パラメータ$${w}$$を最適化する手法である。

上図のように、関数の値が最小になる点の付近において、その点での微分係数は$${x^{(l)} < x_{min}}$$であれば負に、$${x^{(l)} > x_{min}}$$であれば正になる。前者であれば$${x^{(l)}}$$に正の値を、後者であれば負の値を加えれば$${x_{min}}$$に近づくことになる。
よって、現在のパラメータ$${w}$$から$${\frac {\partial E} {\partial \bm{w}}}$$に、学習率$${\epsilon}$$を乗じたものを引いていき、$${w}$$を更新していく方法を勾配降下法と呼ぶ。(下式)
$$
\bm{w}^{(t+1)} = \bm{w}^{(t)} - \epsilon \nabla E\\
\nabla E = \frac {\partial E} {\partial \bm{w}} = \lbrack \frac {\partial E}{\partial \bm{w_1}} \dots \frac {\partial E}{\partial \bm{w_M}} \rbrack
$$
■学習率
学習率が大きすぎる場合、最小値にいつまでもたどり着かず発散してしまう。
学習率が小さすぎる場合、収束するまでに時間がかかってしまう。
学習率の決定、収束性向上のためのアルゴリズムとして、以下のような手法が考えられ、利用されている。
・Momentum
・AdaGrad
・Adadelta
・Adam
■確率的勾配降下法
入力データを一度の学習で全て使用すると、計算コストが非常にかかる場合がある。そのような場合、ランダムに抽出したサンプルを入力として学習を進めて行く方法がある。これを確率的勾配降下法(SGD)と言う。
メリット
・計算コストの軽減
・望まない局所極小解に収束するリスクの軽減
・オンライン学習ができる
■ミニバッチ学習
ランダムに分割したデータの集合(ミニバッチ)$${D_t}$$に属するサンプルの平均誤差を用いて学習を進めていく方法をミニバッチ学習と言う。
メリット
・確率的勾配降下法のメリットを損なわず、CPUを利用したスレッド並列化やGPUを利用したSIMD並列化により計算機の計算資源を有効利用できる。
4-2 実装演習
ネットワーク作成後、下記のコードで重みが更新されることを確認した。
grad = backward(x, d, z1, y)
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]ネットワーク作成と確認のコードは以下。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
#print("shape: " + str(x.shape))
print("")
# ウェイトとバイアスを設定
# ネートワークを作成
def init_network():
network = {}
network['W1'] = np.array([
[0.1, 0.3, 0.5],
[0.2, 0.4, 0.6]
])
network['W2'] = np.array([
[0.1, 0.4],
[0.2, 0.5],
[0.3, 0.6]
])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['b2'] = np.array([0.1, 0.2])
return network
# 順伝播
def forward(network, x):
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = functions.relu(u1)
u2 = np.dot(z1, W2) + b2
y = functions.softmax(u2)
return y, z1
# 誤差逆伝播
def backward(x, d, z1, y):
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_sigmoid_with_loss(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# 訓練データ
x = np.array([[1.0, 5.0]])
# 目標出力
d = np.array([[0, 1]])
# 学習率
learning_rate = 0.01
network = init_network()
y, z1 = forward(network, x)
# 誤差
loss = functions.cross_entropy_error(d, y)
grad = backward(x, d, z1, y)
print("****before****")
for key in network.keys():
print(key)
print(network[key])
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
print("****after****")
for key in network.keys():
print(key)
print(network[key])****before****
W1
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
W2
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
b1
[0.1 0.2 0.3]
b2
[0.1 0.2]
****after****
W1
[[0.1002612 0.3002612 0.5002612 ]
[0.20130599 0.40130599 0.60130599]]
W2
[[0.09895521 0.40104479]
[0.19782336 0.50217664]
[0.2966915 0.6033085 ]]
b1
[0.1002612 0.2002612 0.3002612]
b2
[0.09912934 0.20087066]確かに、重みが更新されることを確認した。
4-3 確認テスト
◆確認テスト①

回答①
#それぞれ以下のコードになる
network[key] -= learning_rate * grad[key]
grad = backward(x, d, z1, y)1-3のファイル内から抜き出した。
◆確認テスト②

回答②
学習データが入ってくるたびに都度パラメータを更新し、学習を進めて行く方法。
◆確認テスト③

回答③
下図のように、エポック$${t}$$の時点の重み$${w^t}$$から計算された誤差を$${w}$$で微分した値に学習率$${\epsilon}$$を掛けた値を$${w^t}$$から引き、この計算結果を次の重み${w^{t+1}}$$として使用することを表している。

5. 誤差逆伝播法
5-1 要点
勾配降下法によりパラメータを更新する際、誤差勾配を計算する必要がある。通常、以下のように微小値$${h}$$を用いて微分を計算する。
$$
\frac {\partial E}{\partial \bm{w_m}} \approx \frac {E(w_m+h)-E(w_m-h)} {2h}
$$
しかし、この方法では順伝播の計算を繰り返し行う必要があり計算負荷が大きい。
ここで、微分の連鎖率を利用して$${\frac {\partial E}{\partial \bm{w}}}$$や$${\frac {\partial E}{\partial b}}$$を変形し、解析的に求めた微分値を使用することで不要な再帰的計算を避けて微分を算出できる。これを誤差逆伝播法と言う。
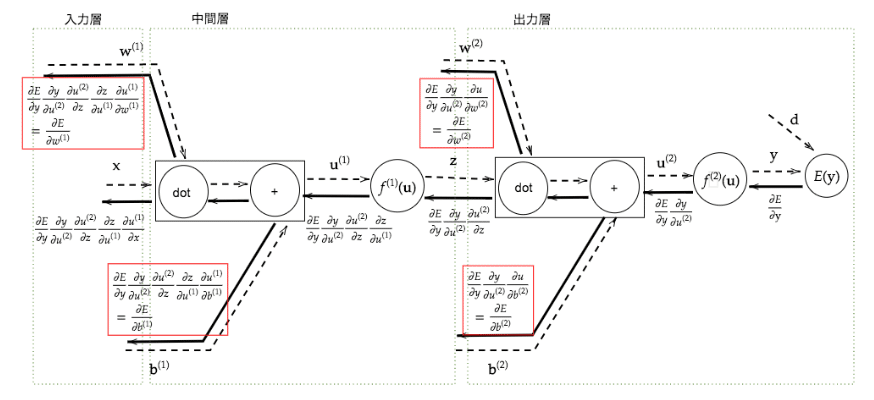
例として、以下のように計算できる。


5-2 実装演習
主要な活性化関数である、シグモイド関数、ReLU関数、平均二乗誤差関数の導関数のコードを確認した。
# シグモイド関数(ロジスティック関数)の導関数
def d_sigmoid(x):
dx = (1.0 - sigmoid(x)) * sigmoid(x)
return dx
# ReLU関数の導関数
def d_relu(x):
return np.where(x > 0, 1, 0)
# 平均二乗誤差の導関数
def d_mean_squared_error(d, y):
if type(d) == np.ndarray:
batch_size = d.shape[0]
dx = (y - d) / batch_size
else:
dx = y - d
return dx5-3 確認テスト
◆確認テスト①

回答①
以下のコードで(※)を付けた部分で過去に計算した結果を保持している。
def backward(x, d, z1, y):
# print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y) #(※)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1) #(※)
delta1 = delta1[np.newaxis, :] #(※)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad◆確認テスト②

回答②
それぞれ
delta2 = functions.d_mean_squared_error(d, y)grad['W2'] = np.dot(z1.T, delta2)