
ポラライズはなぜ強い?~ポラライズのGTO戦略とその優位性~
はじめに
!50いいね超えで新記事執筆いたします!
最近よく聞く「ポラライズ」
そのポラライズが何故強いのかについて、理論的な立場から紐解いていきます。
2022.2.24追記
無料公開にしました。
問題提起:相手の大きなベットにコールすべき?
想像してみてください。
こんなボード↓で、

こんなハンド↓を持っている時。
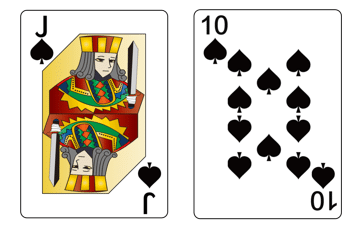
ストレート完成!めちゃくちゃ嬉しいですよね。
でも、相手から300%ポットのオールインがきてしまいました。
相手のハンドレンジにはAA,KK,AK等のナッツ級のハンドがありますが、それらはあなたのハンドレンジにはありません。
めちゃくちゃ嫌ですよね。あなたはコールすべきでしょうか?
いきなり答えを出すのは難しいので、順を追って考えてみましょう。
基礎編①:ポラライズドレンジの優位性を知る
まず、単純化して考えるためにAKQゲームを導入します。

【ルール】
A,K,Qそれぞれ1枚、合計3枚を使ったゲームです。あなたはには必ずKが配られ、相手にはAかQが等確率で配られます。ショーダウンでは、持っているカードが相手より強ければポットを獲得します。その他の設定は下記です。
・ベッティングラウンドは1回限り
・ベットサイズはオールイン限定
・ポット:100bb
・エフェクティブスタック:100bb
・カードの強さ:A>K>Q
相手にはAとQがそれぞれ50%の確率で配られます。
相手のそのハンドレンジに対して、あなたのKは50%のEQ(※1)を持っています。同様に相手のハンドレンジ全体のEQ(※1)も50%です。
※1「EQ」:エクイティ(Equity)。配られたカードをそのままショーダウンした時の勝率
このゲームにおける各プレイヤーの最適な戦略を理解するために、ここからは一問一答形式で進んでいきましょう。
ただし、本記事で言う「最適」とは「持っている情報のもとで自分の利益を最大化するような」という意味です。
-------------------------------------
【Q1】
あなた(K)はOOP(※2)です。自分からベットする最適な頻度はいくつでしょうか?
⑴0% ⑵50% ⑶100%
※2「OOP」:Out of Position。アウトオブポジション。相手より先にアクションするポジションのこと。
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A1】⑴0%
(解説)
あなたがベットをしても、相手はあなたがKを持っていることを知っているので、単純明快な下記戦略を実行するだけで利益を最大化できます。
・相手がAを持っている時 → あなたのKに勝っているのでコール
・相手がQを持っている時 → あなたのKに負けているのでフォールド
つまり、あなたのKでのベットは、あなたが負けている時にだけコールされ、あなたが勝っている時にはフォールドされるだけなので、ベットする誘因がありません。従って、最適なベット頻度は0%となります。
-------------------------------------
-------------------------------------
【Q2】
あなた(K)はIP(※3)です。相手(A,Q)はOOPでチェックしました。あなた(K)のベット戦略は【A1】の0%のまま変わらないでしょうか?それとも変わるでしょうか?
※3「IP」:in Position。インポジション。相手より後にアクションするポジションのこと。
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A2】変わらない
(解説)
ポジションに関係なく、相手はあなたがKを持っていることを知っているので、A1と同様に最適なベット頻度は0%となります。
このゲームにおいて、IPにいることによる優位性は発生しません。
-------------------------------------
-------------------------------------
【Q3】
相手(A,Q)がOOPでAを持っている時、チェックする最適な頻度はいくつでしょうか?
⑴0% ⑵50% ⑶100%
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A3】⑶0%
(解説)
相手がチェックをしても、【A1】と【A2】で見たように、あなたがKでベットすることはありません。従って、相手はAでチェックしてもそれ以上の利益を得ることがないので、チェックせず必ずベットすべきです。
-------------------------------------
-------------------------------------
【Q4】
相手(A,Q)はQを持っている時、ある程度の頻度でベットをするべきです。それはなぜでしょうか?
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A4】
相手(A,Q)はQでのブラフを全くしないと、Aでベットした時にあなた(K)にハンドがばれてフォールドされてしまうから。
(解説)
相手はAを持っている時には必ずベットし、あなたにコールしてもらえばもらうほど利益が増えます。しかし、仮に相手がQでベットしてこないことをあなたが知っていたら、相手のベットは必ずAだとわかるので、100%頻度でフォールドすることができてしまいます。
-------------------------------------
さて、ここまでで明らかになったことをまとめてみます。
【ここまでのまとめ】
・あなた(K)は自分からベットすることはない。
・相手(A,Q)はAでチェックすることはない。
・相手(A,Q)はQで少なからずベットすべき。
このまとめを見ると、あなた(K)の立場はとても不利に思えてきませんか?単純なEQは50%ずつで平等なはずなのに!!!
実際、あなたはKより弱いQにベットされてハンドは勝ってるのにフォールドさせられたり、Aのバリューベットに負けてるのにコールさせられたりすることになります。つまり、お互いに最適な戦略をとった時、相手のEV(※4)はあなたのEVより高いのです。
※4「EV」:イーブイ。Expected Value。期待値のこと。その状況で獲得する利益の平均値。
<EVの式>
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
EQに対するこのEVの偏りは、このAKQゲームがポラライズドレンジvsコンデンスドレンジ(※5)であることに起因しています。
※5【"ポラライズドレンジ"と"コンデンスドレンジ"の説明】
ポラライズドとは「両極化された」という意味で、コンデンスドとは「凝縮された」という意味です。
今回、相手はあなたのハンドレンジ(K)に対して、勝率100%のAと勝率0%のQの2通りを持っており、そのハンドレンジは"ポラライズされている"と言い、そんなハンドレンジのことを"ポラライズドレンジ"と言います。
逆に、あなたは相手のハンドレンジ(A,Q)に対して、勝っているか負けているかわからない勝率50%のKのみを持っており、そのハンドレンジは”コンデンスされている"と言い、そんなハンドレンジのことを"コンデンスドレンジ"と言います。
具体的な説明は後述するとして、この事実を覚えておいてください。
重要事項①:ポラライズドレンジvsコンデンスドレンジにおいて、前者はEV上優位に立つことができる。
基礎編②:ポラライズドレンジの優位性を活かす戦略を知る
さて、ここからはEVを具体的に計算していきます。最終目標は、ポラライズドレンジが利益を最大化する戦略について理解することです。
-------------------------------------
【Q5】
相手(A,Q)が「Aで必ずベットし、Qで全くベットしない」戦略をとった時、あなた(K)の最適な戦略は「相手のベットに必ずフォールドし、それ以外はチェックする」戦略です。その時のあなたのEVはいくらでしょうか?
⑴25bb ⑵50bb ⑶75bb
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A5】⑵50bb
(解説)
Kで勝つ確率(50%)でポット(100bb)を獲得し、Kで負ける確率(50%)で何も失わないので、あなたのEVは100bbの50%=50bbです。細かく計算を見たい人は下の【細かい計算】を読んでください。
ちなみに、あなたが負ける確率50%で相手がポット(100bb)を得るので、相手のEVは100bbの50%=50bbであり、あなたのEVと同等です。あなたのEV+相手のEV=ポット(100bb)が必ず成立します。
重要事項②:あなたのEV+相手のEV=ポット
相手がこの戦略をとった時、相手のEVはあなたのEVより高いわけではないので、少なくとも相手のこの戦略は最適ではなさそうです。
【細かい計算】
<EVの式>は下記です。
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
ここで、各項の値がいくつかを具体的に見てみましょう。
相手がQを持っている時、あなたは必ずショーダウンで勝ちます。この確率は相手にQが配られる確率50%です。よって、【勝つ確率】=50%です。またその時、【追加で得る額】=【ポット】=100bbです。
一方、相手にAが配られる確率50%であなたは負けるので、【負ける確率】=50%です。また、相手がAを持っている時、あなたはベットされたらフォールドし、チェックされたらショーダウンで負けます。いずれにしても【追加で失う額】=0bbです。
上式にこれらを代入して、EV=50bbと分かります。
EV=50% × 100bb - 50% × 0bb = 50bb
-------------------------------------
-------------------------------------
【Q6】
相手(A,Q)が「ハンドに関係なく必ずベットする」戦略をとった時、あなた(K)の最適な戦略は「必ずコールする」戦略です。
その時のあなたのEVはいくらでしょうか?
⑴25bb ⑵50bb ⑶75bb
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A6】⑵50bb
(解説)
相手はハンドに関わらず100%頻度でベットし、あなたは100%頻度でコールすることになります。Kで勝つ確率(50%)でポット(100bb)+相手のベット額(100bb)を獲得し、Kで負ける確率(50%)であなたのコール額(100bb)を追加で失うので、あなたのEVは50bbです。細かく計算を見たい人は下の【細かい計算】を読んでください。また、重要事項②の通り、あなたのEV+相手のEV=ポット(100bb)なので、相手のEVは50bbです。
相手がこの戦略をとった時も、相手のEVはあなたのEVより高いわけではないので、少なくともこの戦略は最適ではなさそうです。
【細かい計算】
<EVの式>は下記です。
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
ここで、各項の値がいくつかを具体的に見てみましょう。
相手にQが配られる確率50%であなたは勝つので、【勝つ確率】=50%です。この時、【追加で得る額】=【ポット】+【ベット額】=200bbです。
一方、相手にAが配られる確率50%であなたは負けるので、【負ける確率】=50%です。この時、【追加で失う額】=【コール額】100bbです。
上式にこれらを代入して、EV=50bbと分かります。
EV=50% × 200bb - 50% × 100bb = 50bb
-------------------------------------
【A5】と【A6】から推察できるように、相手のQでのブラフベットの頻度が最適よりも多いならコールEVはフォールドEVよりも高くなり、あなたは相手のベットに100%コールすることが最適となります。逆に、相手のQでのブラフが最適な頻度よりも少ないならあなたのフォールドEVはコールEVよりも高くなり、あなたは相手のベットに100%フォールドすることが最適になります。
-------------------------------------
【Q7】
相手(A,Q)がQで最適な頻度でブラフをする戦略をとった時、相手のベットに対するあなた(K)のコールEVとフォールドEVはどちらが高いでしょうか?
⑴コールEV>フォールドEV(コールEVの方が高い)
⑵コールEV<フォールドEV(フォールドEVの方が高い)
⑶コールEV=フォールドEV(同じ)
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A7】⑶コールEV=フォールドEV(同じ)
(解説)
まず、重要事項②の通り、あなたのEV+相手のEV=ポット(100bb)です。このことから、あなたのEVが上がるほど相手のEVが下がることが分かります。
ここで、もしあなたのコールEVがフォールドEVより高い場合、あなたはコール頻度を100%にまで上げることであなた自身のEVを最大化し、相手のEVを下げることができます。一方で、もしあなたのフォールドEVがコールEVより高い場合も同様で、あなたはフォールド頻度を100%にまで上げることであなた自身のEVを最大化し、相手のEVを下げることができます。このように、あなたが戦略を調整することで相手のEVが変わるような相手の戦略は最適ではありません。裏を返すと、相手が最適な頻度でベットしてくる時、あなたはコールしてもフォールドしても、それらのEVが同じとなるのです。あなたのこの状態のことを、コールとフォールドについてindifferent(無関係・無差別)であると言います。
重要事項③:複数のアクションのEVが等しい状態の時「それらのアクションについてindifferentである」と言う。
-------------------------------------
-------------------------------------
【Q8】
相手(A,Q)がQを持っている時、その最適なベット頻度はいくつでしょうか。
ヒント:あなた(K)はコールとフォールドについてindifferentとなります。
⑴33.3% ⑵50% ⑶66.6%
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A8】⑵50%
相手は最適戦略において、Qで50%の頻度でベットしてきます。
【導出過程】
<EVの式>は下記です。
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
あなたのコールEV=フォールドEVとなるような相手のQのベット頻度を求めます。
<フォールドEV>
あなたがフォールドする時、【追加で得る額】も【追加で失う額】も0bbなので、フォールドEV=0bbです。
<コールEV>
まず上記から、コールEV=フォールドEV=0bbとおけます。また、
【勝つ確率】=【相手がベットするQの数】
【負ける確率】=【相手がベットするAの数】
と置き換えても<EVの式>は成立します。さらに、コールして勝つ時【追加で得る額】=【ポット】+【ベット額】であり、コールして負ける時【追加で失う額】=【コール額】です。これらを<EVの式>に代入して移項すると、下式が成立します。
【相手がベットするQの数】/【相手がベットするAの数】=【コール額】/(【ポット】+【ベット額】) ・・・★
この式が成立するような頻度で相手がQでベットすれば、あなたはコールとフォールドについてindifferentとなるということです。
このゲームでは、【ポット】=【コール額】=【ベット額】=100bbであるので、これを★式に代入すると下式になります。
【相手がベットするQの数】/【相手がベットするAの数】=1/2
この式から、【相手がベットするQの数】1つにつき【相手がベットするAの数】が2つであることがわかります。相手はAの100%でベットするので、上式を成立させるために相手はQの50%でベットすることになります。
★式は後述の応用編で再び利用します。
-------------------------------------
【Q9】
相手(A,Q)が最適戦略(Aの100%とQの50%でベットする)を取る時、あなたのEVはいくつでしょうか?
⑴0bb ⑵25bb ⑶50bb
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A9】⑵25bb
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
まず、相手はAの100%と、Qの50%でベットします。相手のこの最適戦略に対して、あなたはコールしてもフォールドしてもEVが変わらないので、計算を簡単にするために全てフォールドすると仮定します。すると、あなたが勝つ確率は、相手がQでチェックしてショーダウンで勝つ確率なので、【勝つ確率】=50/200=1/4です。その時、ポットの100bbを得るので、【追加で得る額】=100bbです。また、【負ける確率】=フォールドする確率=3/4であり、このとき【追加で失う額】=0bbです。これらを上式に代入すると25bbとなります。
EV=1/4 × 100bb - 3/4 × 0bb = 25bb
また、重要事項②の通り、あなたのEV+相手のEV=ポット(100bb)なので、相手のEVは75bbです。なんと、相手のEVはあなたのEVの3倍もあるのです!
-------------------------------------
-------------------------------------
【Q10】
相手(A,Q)が最適戦略(Aの100%とQの50%でベットする)を取る時、あなた(K)はコールとフォールドについてindifferentとなります。とは言え、あなたが相手のベットに100%フォールドする戦略を取る場合、相手はその戦略を再構築することでEVを更に上げることができます。その再構築された戦略とはどのようなものでしょうか?
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A10】100%ベットする
あなたが100%フォールドするなら、相手は100%ベットすることで毎回ポットを獲得し、EVを100bbまで上げることができます。逆にもしあなたが100%コールするとしたら、相手はQでのブラフ頻度を0%にまで下げ、EVを100bbまであげることができます。
つまり、あなたのフォールド頻度が高過ぎる場合、相手のQでベットするEVがチェックするEVより高くなり、相手はQでのベット頻度を100%にまで上げることでEVを最大化し、あなたのEVを下げることができます。もしあなたのコール頻度が高過ぎる場合も同様で、相手のQでチェックするEVがベットするEVより高くなり、相手はQでのチェック頻度を100%にまで上げることでEVを最大化し、あなたのEVを下げることができます。このように、相手が戦略を調整することであなたのEVが下がり得るようなあなたの戦略は最適ではありません。裏を返すと、あなたが最適な頻度でコールをする時、相手はQでベットしてもチェックしても、それらのEVが同じとなるのです。重要事項③で触れた通り、相手のこの状態のことを、Qでのベットとチェックについてindifferent(無関係・無差別)であると言います。
-------------------------------------
-------------------------------------
【Q11】
相手(A,Q)が最適戦略(Aの100%とQの50%でベットする)を取る時、あなた(K)の最適なコール頻度はいくつでしょうか。
ヒント:相手のQはベットとチェックについてindifferentとなります。
⑴33.3% ⑵50% ⑶66.6%
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A11】⑵50%
あなたは最適戦略において、50%の頻度でコールします。
【導出過程】
<EVの式>は下記です。
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
相手のQがベットEV=チェックEVとなるようなあなたのコール頻度を求めます。
<QでのチェックEV>
相手がチェックする時、【追加で得る額】も【追加で失う額】も0bbなので、チェックEV=0bbです。
<QでのベットEV>
まず上記から、ベットEV=チェックEV=0bbとおけます。また、
【勝つ確率】=【あなたがフォールドする確率】
【負ける確率】=【あなたがコールする確率】
と置き換えても<EVの式>は成立します。さらに、ベットして勝つ時【追加で得る額】=【ポット】であり、ベットして負ける時【追加で失う額】=【ベット額】です。これらを<EVの式>に代入して移項すると、下式が成立します。
【あなたがフォールドする確率】/【あなたがコールする確率】=【ベット額】/【ポット】 ・・・★★
この式が成立するような頻度であなたがコールすれば、相手はQでのベットとチェックについてindifferentとなるということです。
このゲームでは、【ポット】=【ベット額】=100bbであるので、これを★★式に代入すると下式になります。
【あなたがフォールドする確率】/【あなたがコールする確率】=1/1
上式を成立させるために
この式から、【あなたがフォールドする確率】=【あなたがコールする確率】であることがわかります。上式を成立させるためにあなたは50%の確率でコールし、残りの50%の確率でフォールドすることが最適であることになります。
★★式は後述の応用編で再び利用します。
-------------------------------------
-------------------------------------
さて、ここまでで明らかになったことをまとめてみます。
最適戦略においては、相手が複数のアクションについてIndifferentになるよう各プレイヤーが自分のアクション頻度を調整します。もし片方のプレイヤーのアクション頻度のバランスが崩れると、もう片方のプレイヤーに一方的にEVを上昇させるような戦略調整の余地を与えてしまうことになり、これは最適とは言えなくなります。
言い方を変えると、片方のプレイヤーが最適戦略を取る時、もう片方のプレイヤーはどのように戦略を変更しても、自分ないしは相手のEVを変えることができません。また、お互いがそのような最適戦略を採用することで、どちらのプレイヤーもお互いのEVを変える余地がなくなります。このような均衡状態のことをナッシュ均衡と言い、特にそのようなお互いの戦略のことをGTO(※6)戦略と言います。これとは対照的に、相手のGTO戦略からはずれた戦略に対して自分の戦略を最適化することで利益を最大化することをexploit(※7)すると言い、特にそのような戦略のことをexploit戦略と言います。
※6「GTO」:ジーティーオー。Game Theory Optimal。「ゲーム理論上最適な」という意味。
※7「exploit」:エクスプロイト。「搾取する」という意味。
【お互いの戦略とEVまとめ】
・相手(A,Q)はGTO戦略において、Aの100%とQの50%でベットし、Qの残りの50%でチェックする。
・あなた(K)はGTO戦略において、相手のベットに対して50%でコールし、残りの50%でフォールドし、相手のチェックに対しては100%チェックする。
・お互いがGTO戦略をとった時、相手のEV=75bbであり、あなたのEV=25bbである。
基礎編③:ポラライズドレンジの優位性と戦略を計算ソフトで確認する
基礎編の締めとして、ここまでで導出したAKQゲームにおけるGTO戦略が正しいことを、計算ソフトのpiosolverで確認してみます。
ただし、今回のAKQゲームと同様のシチュエーションを再現するために、OOPのハンドレンジはKK、IPのハンドレンジはAA,QQ、ボードは2,2,2,2,3、アクションはリバーのみとしています。↓

KK側は、自分からベットすることはありません。(緑色はチェックを表しています。)↓
【KK側のアクション】
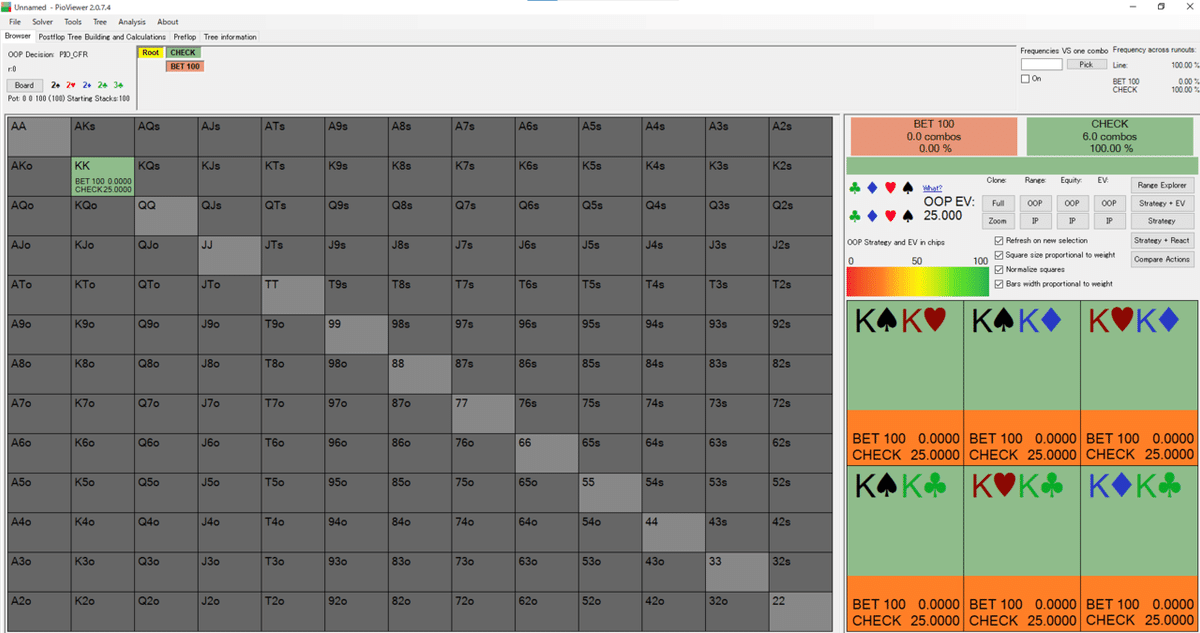
また、EVは25です(↓赤枠)。
【ゲーム開始時点のKK側のEV】

AA,QQ側は、AAの100%とQQの50%でベットし、QQの残りの50%でチェックします。(赤色はベット、緑色はチェックを表しています。)↓
【AA,QQ側のアクション】

また、ハンドレンジ全体のEVは75であり(↓赤枠)、Qはベットとチェックについてindifferent(どちらもEV=0)となっていて(↓黄枠)、50%ずつの頻度で各アクションを取ります。
【ゲーム開始時点のAA,QQ側のEV】

KK側はベットされた時、EVは0であり(↓赤枠)、コールとフォールドについてindifferent(どちらもEV=0)となっていて(↓黄枠)、50%ずつの頻度で各アクションを取ります。(緑色はチェック、青色はフォールドを表しています。)
【ベットに対するKK側のリアクション】

【ベットに対するKK側のEV】

※CALLのEVが厳密に0でないのは、piosolverの許容計算誤差によるもの。
以上、piosolverでの計算でも、これまで見てきた計算結果が正しいことが確認できました。AKQゲームの解説はここまでとします。
応用編①:ポラライズドレンジvsコンデンスドレンジの戦略を一般化する
ここまでであなたは、ポラライズドレンジvsコンデンスドレンジとしてのAKQゲームにおけるGTO戦略の全貌を理解しました。その理解を応用して、より一般的なポラライズドレンジvsコンデンスドレンジにおいても簡易的なGTO戦略を生み出せるようにしましょう。
そのためにここで、前述の★式と★★式を公式化していきます。
<★式の公式化>
【相手がベットするQの数】/【相手がベットするAの数】=【コール額】/(【ポット】+【ベット額】) ・・・★
ここで、下記4つの文字を定義します。
・【相手がベットするQの数】=【相手がベットするブラフコンボ数】=B
・【相手がベットするAの数】=【相手がベットするバリューコンボ数】=V
・【コール額】=【ベット額】=b
・【ポット】=p
これらを★式に代入すると、下記の(公式1)が得られます。

・・・(公式1)
<★★式の公式化>
【あなたがフォールドする確率】/【あなたがコールする確率】=【ベット額】/【ポット】 ・・・★★
ここで、下記4つの文字を定義します。
・【あなたがコールする確率】=C
・【あなたがフォールドする確率】=1-C
・【コール額】=【ベット額】=b
・【ポット】=p
これらを★★式に代入して、
(1-C)/C=b/p
⇔p(1-C)=bC
⇔p-pC=bC
⇔p=(p+b)C
⇔下記の(公式2)が得られます。

・・・(公式2)
応用編②:ポラライズドレンジvsコンデンスドレンジの戦略の7つのエッセンス
前述の(公式1)及び(公式2)には完全なポラライズドレンジvsコンデンスドレンジにおけるGTO戦略のエッセンスが詰まっています。それらのエッセンスを以下に1⃣~7⃣として列挙します。
(公式1)のエッセンス


ポラライズレンジ側はGTO戦略において、
1⃣B:Vの比がb:(b+p)の比に等しくなるようにする。
2⃣B<Vが常に成立する。(なぜなら、b<p+bであるから。)
⇒ポラライズドレンジ側がバリューよりも多くブラフを打っている場合、それはGTO戦略になり得ない。
3⃣pに対してbを大きくするほど、Vに対するBの値が大きくなっていき、B:V=1:1に近づいていく。
⇒bを大きくするほどブラフをたくさん打てるようになる。コンデンスドレンジ側が追加の利益を得るのはポラライズドレンジ側がチェックする場合のみなので、ポラライズドレンジ側はbを可能な限り大きくすることでブラフを高頻度で打つことが最適である。
(公式2)のエッセンス


コンデンスドレンジ側はGTO戦略において、
4⃣p/(b+p)の頻度でコールする。
5⃣pに対するbが大きいほど、コールすべき頻度が小さくなっていき、0に近づいていく。
※(公式2)におけるCは一般的なポーカー用語で言うMDF(Minimum Defence Frequency)と同一のものです。
(公式1)×(公式2)のエッセンス
6⃣下式の通り、B/VとCの和は常に1となる。

⇒B/Vを求めれば、1からその値を引くことでCを求めることができる。逆に、Cを求めれば、1からその値を引くことでB/Vを求めることができる。
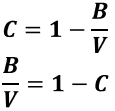
7⃣ポラライズドレンジ側のブラフの必要成功率はb/(p+b)である。
コンデンスドレンジ側のフォールド頻度FはF=1-Cであるので、下式が成立する。

⇒ポラライズドレンジ側のブラフベットは、コンデンスドレンジ側にb/(p+b)の頻度でフォールドさせることになる。より実戦的に言うと、ポラライズドレンジ側のブラフの必要成功率はb/(p+b)であり、これはポットオッズに一致している。
これは考えてみれば当然のことである。なぜなら、ポラライズドレンジ側はbを追加でリスクにさらしp+bを獲得しに行くので、ブラフ成功時にはベットに対して(p+b)/b倍のリターンがあるが、ブラフ全体のEVはGTO戦略上では0となるため、リターンの倍率の平均値は1となる必要があって、その必要成功率はリターンの逆数のb/(p+b)となるからである。
上記7つのエッセンスは、ポーカーをプレイしたり勉強したりする上での最重要な土台となります。計算の背景を理解した上で覚えてしまって損はないでしょう。
実践編①:一般化したポラライズドレンジvsコンデンスドレンジ戦略を活用して問題を簡易的に解く
さて、ここからは冒頭で提議した問題に立ち返って考えてみましょう。
-------------------------------------
<再掲>
こんなボード↓で、

こんなハンド↓を持っている時。

ストレート完成!めちゃくちゃ嬉しいですよね。
でも、相手から300%ポットのオールインがきてしまいました。
相手のハンドレンジにはAA,KK,AK等のナッツ級のハンドがありますが、それらはあなたのハンドレンジにはありません。
めちゃくちゃ嫌ですよね。あなたはコールすべきでしょうか?
-------------------------------------
ここで、あなたと相手のハンドレンジを、お互いにブロッカーを持たない完全なポラライズドレンジvsコンデンスドレンジであると仮定して、下記のように想定します。
【相手のハンドレンジ】

バリュー:AA(3),KK(1),AK(6),KQ(6)、計16コンボ
ブラフ:99(6),88(6),77(6),66(6)、計24コンボ
合計40コンボ
【あなたのハンドレンジ】

55(3),JT(16)、合計19コンボ
ここで、各プレイヤーのハンドレンジ全体及び各ハンドのEQは下記の通りであり、完全なポラライズドレンジvsコンデンスドレンジの形になっていることが分かります。
【相手の各ハンドのEQ】

【あなたのハンドレンジのEQ】

さて、ここでお互いのGTO戦略を導き、その正当性をpiosolverで確認してみましょう。
前提として、相手は300%ポットのオールインをしてきていることに注意しましょう。
まず(公式1)を利用して、

・・・(公式1)
B/V=300/(100+300)=3/4
従って、相手はバリュー4つに対してブラフ3つを混ぜてオールインします。
今回、相手はナッツを16コンボ持っておりその全てでオールインしてくるので、オールインすべきブラフハンドはその3/4の12コンボであり、これはハンドレンジ内にある24コンボのブラフハンドの50%であるはずです。
piosolverでアクション頻度を見ると、これが下記の通り正しいことが確認できます。
【相手の各ハンドのアクション頻度】

次に(公式2)を利用して、

・・・(公式2)
C=100/(100+300)=1/4
従って、あなたは相手のこのベットに対して、ハンドレンジの1/4でコールする必要があります。piosolverでアクション頻度を見ると、これが下記の通り正しいことが確認できます。
【あなたの各ハンドのアクション頻度】

以上より、JTsにおいて『あなたはコールすべきでしょうか?』という問いに対する回答は「1/4の頻度でコールすべき」となります。
実践編②:一般化したポラライズドレンジvsコンデンスドレンジ戦略を活用して問題を現実的に解く
実践編①においては、あなたと相手のハンドレンジをお互いにブロッカーを持たない完全なポラライズドレンジvsコンデンスドレンジであると仮定して計算しました。しかし、これは現実のNLHにおいてはほぼあり得ないような強引な仮定であると言えます。
ここからは、より現実に近い想定レンジを使って、相手にトリプルバレルでちょうど300%ポットのオールインを打たれた際のこの問題におけるGTO戦略を、piosolverで追及していきましょう。
【相手のハンドレンジ(UTGオープンレンジを想定)】

【あなたのハンドレンジ(UTGオープンに対するBBコールレンジを想定)】
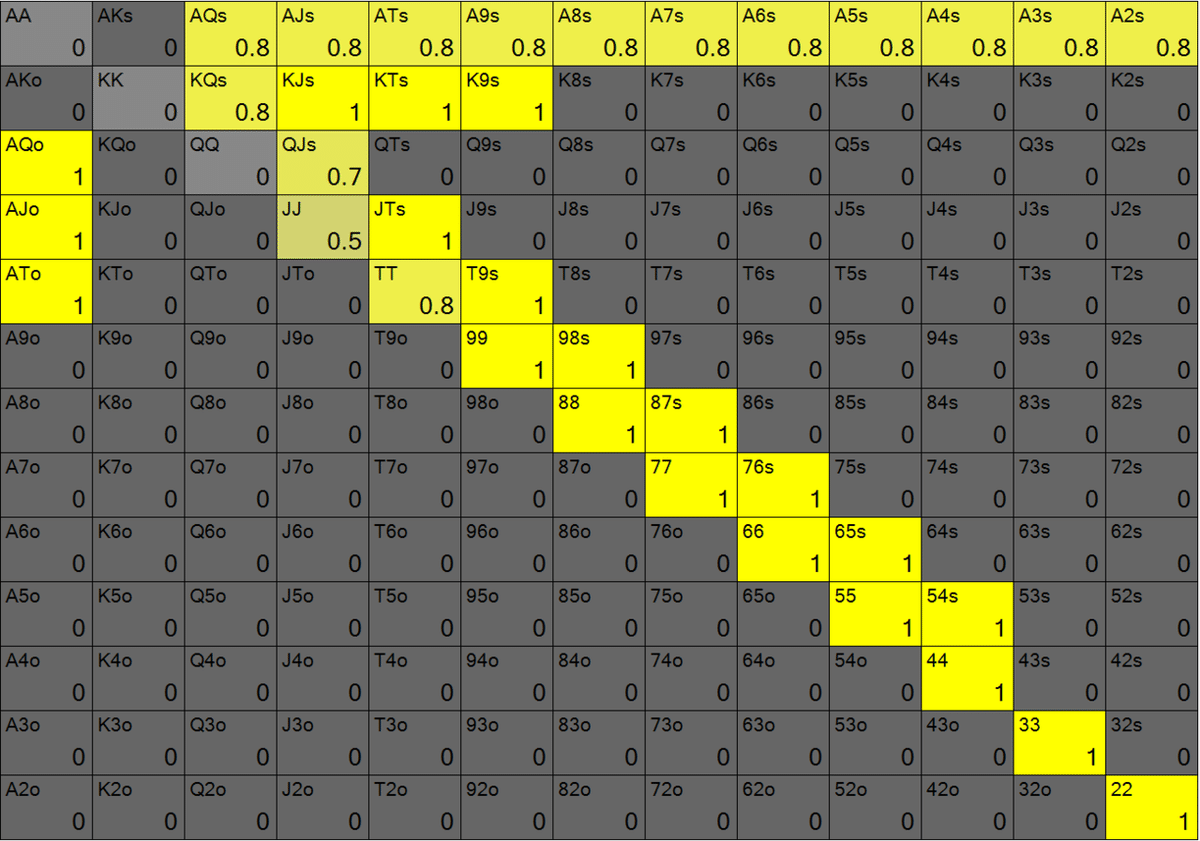
【計算の設定】
計算の設定は下記キャプチャの通りです。

相手の各ストリートのベットサイズは単一とし、トリプルバレルでちょうど300%ポットのオールインとなるようそれらのサイズを、フロップ:25%、ターン:100%、リバー:300%としています。また、あなたにベットの選択肢は与えていません。
(「こんなのまだまだ現実的な設定じゃないぞ!」という反論が聞こえてきそうですが、今回の着眼点はマルチストリートにおけるGTO戦略ではなく、あくまでリバーにおいて300%ポットのオールインを受けた際のGTO対抗戦略であるので良しとしています。)
さて、上記設定で相手がダブルバレルを打ってそれをあなたがコールし、リバー(Ks)が落ちた時点の、各プレイヤーのハンドレンジとそのEQを見てみましょう。
【あなたのハンドレンジとそのEQ】


【相手のハンドレンジとそのEQ】


この時点のTotal Equity(ハンドレンジ全体のEquity)は、あなたの方が相手より大きいです。これは自然なことで、なぜなら、あなたは相手のフロップとターンの2回のベットに対してEQの比較的高いハンドでコールし、EQの比較的低いハンドの大部分はフォールドしているからです。
しかし、あなたのハンドレンジ内のハンドはEQが50%程度のハンド(黄色系のマスのハンド)が大多数であり、つまりハンドレンジがコンデンスされている一方で、相手のハンドレンジはEQが100%に近いハンド(緑系のマスのハンド)とEQが0%に近いハンド(赤系のマスのハンド)で構成されており、つまりハンドレンジがポラライズされています。このような相手の状態を、「ポラライゼーションアドバンテージがある」と言います。ポラライゼーションアドバンテージがある時は、ベットサイズを大きくすることでEVを大きくすることができるので、あなたは不利な状態と言えます。
続いて、お互いのGTO戦略を導き、その正当性をpiosolverで確認してみましょう。
まず、相手の戦略について見ていきます。
(公式1)を利用して、

・・・(公式1)
B/V=300/(100+300)=3/4
従って、相手はバリュー4つに対してブラフ3つを混ぜてオールインします。
今回、相手はナッツ級ハンドを22.6コンボ持っておりその全てでオールインしてくるので、オールインすべきブラフハンドはその3/4の16.95コンボであるはずです。
piosolverでアクション頻度を見ると、下記からわかるように、これが厳密には正しくないことが分かります。
【相手の各ハンドのアクション頻度】

【相手のオールインハンドレンジ内訳】

次に、あなたの戦略を見ていきます。
(公式2)を利用して、

・・・(公式2)
C=100/(100+300)=1/4
従って、あなたは相手のこのベットに対して、ハンドレンジの1/4でコールする必要があります。piosolverでアクション頻度を見ると、これが下記の通り厳密には正しくないことが確認できます。
【あなたの各ハンドのアクション頻度】

【あなたのハンドレンジ全体のアクション頻度】

とは言え、JTsのディフェンス頻度に着目すると、下記の通り全体としては26.89%でコールする戦略となっており、『あなたはコールすべきでしょうか?』という問いに対する回答は「だいたい1/4の頻度でコールすべき」と言えそうです。
【あなたのJTsのアクション頻度】

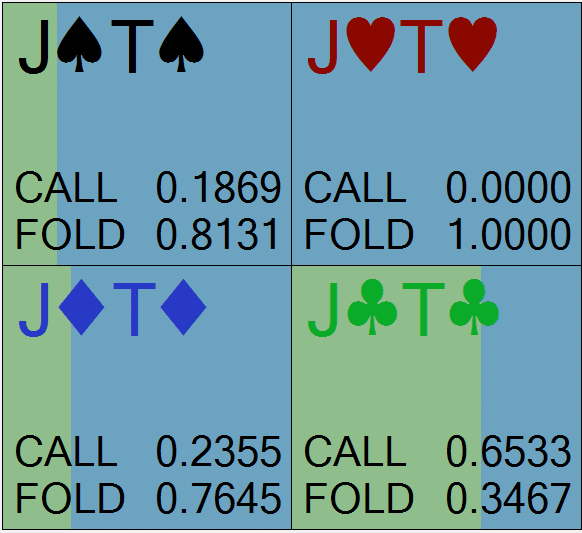
以上から、より現実的な想定においては、公式から導いたGTO戦略通りに厳密になっていないことが発見されました。ここで、新たに浮き彫りとなった疑問点を下記に列挙します。
疑問❶
相手は、(公式1)から導出した値よりも少ない頻度でしかブラフを打っていないのは何故か。
疑問❷
あなたは、(公式2)から導出した値よりも少ない頻度でしかコールをしないのは何故か。
これらの疑問はブロッカーを考慮することで説明がつきます。
実践編③:ブロッカーを加味したポラライズドレンジvsコンデンスドレンジ戦略を考える
疑問❶と疑問❷に説明を与えるために、設定の異なるトイゲームをいくつか導入しながら、ブロッカーについて考えていきましょう。
ただし、この章における各ゲームにおいて、各プレイヤーに配られるハンドのうち♠が含まれるものは存在しないものとし、ポット=100、エフェクティブスタック=300とします。
0⃣AA,JJvsKK,QQゲーム
~ブロッカーなしの場合(復習)~
相手のハンドレンジ:AhAd,AdAc,AcAh,JhJd,JdJc,JcJhの6コンボ
あなたのハンドレンジ:KhKd,KdKc,KcKh,QhQd,QdQc,QcQhの6コンボ
ボードは下記の通り。
-------------------------------------
【Q12】
お互いのGTO戦略はどんなものでしょうか。
ヒント:AKQと同様に求められます。
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A12】
相手はAAのすべてとJJの3/4でオールインし、あなたはKKとQQそれぞれの1/4でコールする。
【導出過程】
(公式1)を利用して、

・・・(公式1)
B/V=300/(100+300)=3/4
従って、相手はAAの3/4でJJでのブラフを打ちます。
(公式2)を利用して、

・・・(公式2)
C=100/(100+300)=1/4
従って、あなたは相手のこのベットに対して、ハンドレンジの1/4でコールします。これはpiosolverで確認しても、下記の通り正しいことが分かります。
【相手の各ハンドのアクション頻度】

【あなたの各ハンドのアクション頻度】

-------------------------------------
1⃣AA,JJvsAKs,QQゲーム
~バリューブロッカーがある場合~
相手のハンドレンジ:AhAd,AdAc,AcAh,JhJd,JdJc,JcJhの6コンボ
あなたのハンドレンジ:AhKh,Addc,AcKh,QhQd,QdQc,QcQhの6コンボ
ボードは下記の通り。

あなたのAKsは相手のAAの一部をブロックしています。
-------------------------------------
【Q13】
【A12】に比べて、相手の戦略はどのように変化するでしょうか。
⑴ブラフを増やす ⑵ブラフを減らす ⑶変わらない
【Q14】
【A12】に比べて、あなたの戦略はどのように変化するでしょうか。
⑴コールを増やす ⑵コールを減らす ⑶変わらない
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A13】
⑵ブラフを減らす
【A14】
⑶変わらない
下記のpiosolverによる計算結果を見てみると、相手のJJでのベット頻度は【A13】の通り3/4から1/4に減っており、あなたのコール頻度は【A14】の通り1/4で変わっていません。ただし、あなたは優先的にAKsをコールし、QQをコールすることはありません。
【相手の各ハンドのアクション頻度】

【あなたの各ハンドのアクション頻度】

このGTO戦略を取る理由をひとつずつ紐解いていきましょう。
まず、あなたが優先的にAKhをコールする理由について。
あなたが仮にAhKhを持っている時、相手のレンジ内のAAはAdAcに限られ、あなたから見た相手のAAコンボ数は3コンボから1コンボに減ります。これは他のAKsを持っている時も同様です。
【あなたのAhKhがブロックする相手のAA】

従って、QQを持っている時に比べてAKsを持っている時の方が、相手のベットしてきているハンドがAAである確率が下がりJJである確率が上がります。つまり、AKsのコールEV>QQのコールEVとなるため、あなたはAKsを優先的にコールすることになります。
次に、あなたのコール頻度について。
あなたのコール頻度は【A14】の通り変わらず1/4です。これは(公式2)から導出される値ですが、この値はそもそも、相手のブラフハンドであるJJがベットとチェックについてindifferent(ベットEV=チェックEV=0)となるように調整されたものです。ここで、公式に頼らずベットEVを求めて考えてみます。<EVの式>は下記であり、
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
相手のJJでのベットEVが0となる条件を求めると、
0=【あなたがフォールドする確率】×100-【あなたがコールする確率】×300
⇔【あなたがフォールドする確率】/【あなたがコールする確率】=1/3
となり、1/4の頻度でコールすべきことがこの計算通りであることが確認できました。相手にベットされた時のあなたの戦略を総合すると、あなたはAKsの1/2でコールしQQの全てでフォールドすることで、レンジ全体のコール頻度が1/4になるようにします。
最後に、相手のJJでのベット頻度について。
【A13】の通り相手のJJでのベット頻度は(公式1)から導出される3/4から1/4に減っています。この値はそもそも、あなたのブラフキャッチハンドがコールとフォールドについてindifferent(コールEV=フォールドEV=0)となるように調整されたものです。ここで、公式に頼らずコールEVを求めて考えてみます。<EVの式>は下記であり、
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
あなたがコールするハンドはAKsのみであることを考慮して、あなたのAKsでのコールEVが0となる条件を求めると、
0=【相手がベットするJJの数】×400-【相手がベットするAAの数】×300
⇔【相手がベットするJJの数】/【相手がベットするAAの数】=3/4
となります。今、あなたのAKsは相手のAAを3コンボから1コンボに減らしているので、【相手がベットするAAの数】=1コンボであり、従って【相手がベットするJJの数】=3/4コンボであれば、あなたのAKsはコールとフォールドについてindifferentとなります。この3/4コンボという値は、3コンボあるJJの1/4に該当するので、この計算がpiosolverの結果と合致することが確認できました。
以上から、下記のことが言えます。
重要事項⑤:(公式1)におけるVの値は、ポラライズ側のバリューハンドをコンデンス側のブラフキャッチャーがブロックするコンボ数だけ減らした後のバリューコンボ数として計算する必要があり、それに伴ってBの値も低下する。
2⃣AA,JJvsKK,QJsゲーム
~ブラフブロッカーがある場合~
相手のハンドレンジ:AhAd,AdAc,AcAh,JhJd,JdJc,JcJhの6コンボ
あなたのハンドレンジ:KhKd,KdKc,KcKh,QhJh,QdJd,QcJc,の6コンボ
ボードは下記の通り。

あなたのQJsは相手のJJの一部をブロックしています。
-------------------------------------
【Q15】
【A12】に比べて、相手の戦略はどのように変化するでしょうか。
⑴ブラフを増やす ⑵ブラフを減らす ⑶変わらない
【Q16】
【A12】に比べて、あなたの戦略はどのように変化するでしょうか。
⑴コールを増やす ⑵コールを減らす ⑶変わらない
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A15】
⑶変わらない
【A16】
⑵コールを減らす
下記のpiosolverによる計算結果を見てみると、相手のJJでのベット頻度は【A15】の通り3/4で変わらず、あなたのコール頻度は【A16】の通り1/4から1/6に減っています。ただし、あなたは優先的にKKをコールし、QJsをコールすることはありません。
【相手の各ハンドのアクション頻度】

【あなたの各ハンドのアクション頻度】
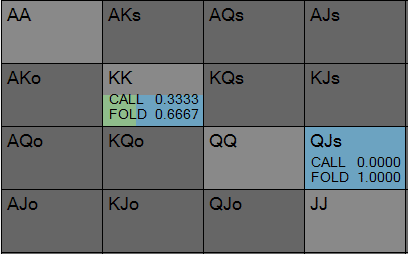
このGTO戦略をひとつずつ紐解いていきましょう。
まず、あなたが優先的にKKをコールする理由について。
あなたが仮にQhJhを持っている時、相手のレンジ内のQQはQdQcに限られ、あなたから見た相手のQQコンボ数は3コンボから1コンボに減ります。これは他のQJsを持っている時も同様です。
【あなたのQhJhがブロックする相手のJJ】

従って、KKを持っている時に比べてQJsを持っている時の方が、相手のベットしてきているハンドがAAである確率が上がりJJである確率が下がります。つまり、KKのコールEV>QJsのコールEVとなるため、あなたはKKを優先的にコールすることになります。
次に、あなたのコール頻度について。
【A16】の通りあなたのコール頻度は(公式2)から導出される1/4から1/6に減っています。この値はそもそも、相手のブラフハンドであるJJがベットとチェックについてindifferentとなるように調整されたものです。ここで、公式に頼らずEVを求めて考えてみます。<EVの式>は下記であり、
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
相手のJJでのベットEVが0となる条件を求めると、
0=【あなたがフォールドする確率】×100-【あなたがコールする確率】×300
⇔【あなたがフォールドする確率】/【あなたがコールする確率】=1/3
となり、あなたは1/4の頻度でコールすべきことが計算できました。ただし、相手のJJはあなたのQJsを3コンボから1コンボに減らしているので、KKの3コンボ+QJsの1コンボのうちの1/4の頻度でコールすることがJJのベットをindifferentにします。あなたはQJsよりKKを優先してコールするので、結果的にKKの1/3でコールすることになります。あなたの戦略を総合すると、相手にベットされた時、あなたはKKの1/3でコールしQJsの全てでフォールドすることで、レンジ全体のコール頻度が1/6になるようにするのです。
最後に、相手のJJでのベット頻度について。
相手のJJでのベット頻度は【A15】の通り変わらず3/4です。これは(公式2)から導出される値ですが、この値はそもそも、あなたのブラフキャッチハンドがコールとフォールドについてindifferentとなるように調整されたものです。ここで、公式に頼らずEVを求めて考えてみます。<EVの式>は下記であり、
EV=【勝つ確率】×【追加で得る額】-【負ける確率】×【追加で失う額】
あなたのKKでのコールEVが0となる条件を求めると、
0=【相手がベットするJJの数】×400-【相手がベットするAAの数】×300
⇔【相手がベットするJJの数】/【相手がベットするAAの数】=3/4
となり、相手はJJの3/4の頻度でベットすべきことが、この計算通りであることが確認できました。
以上から、下記のことが言えます。
重要事項⑥:(公式2)におけるCの値は、コンデンス側のブラフキャッチャーがポラライズ側のブラフハンドによりブロックされるコンボ数だけ減らした後の全体コンボ数に対するコール頻度として計算されるべきものであり、そのブロッカーを考慮しない値よりも小さくなる。
-------------------------------------
3⃣AA,JJvsAKs,QJsゲーム
~バリューブロッカーとブラフブロッカーがある場合~
相手のハンドレンジ:AhAd,AdAc,AcAh,JhJd,JdJc,JcJhの6コンボ
あなたのハンドレンジ:AhKh,Addc,AcKh,QhJh,QdJd,QcJc,の6コンボ
ボードは下記の通り。

あなたのAKsは相手のAAの一部をブロックし、あなたのQJsは相手のJJの一部をブロックしています。
-------------------------------------
【Q17】
お互いのGTO戦略はどんなものでしょうか。
(答えは下です。考えたい人は止まってください。)
↓
↓
↓
↓
↓
【A17】
相手はAAのすべてとJJの1/4でオールインし、あなたはAKsの1/3でコールしそれ以外をフォールドする。
この戦略はつまり、2⃣と3⃣のふたつのゲームのブロッカー要素を複合したものです。
【相手の各ハンドのアクション頻度】

【あなたの各ハンドのアクション頻度】

このことから、重要事項④と重要事項⑤は重ね合わせて考えて良いことがわかります。
-------------------------------------
<疑問❶と疑問❷への説明>
まとめとして、疑問❶と疑問❷についての説明を与えます。
まず、疑問❶を再掲します。
疑問❶
相手は、(公式1)から導出した値よりも少ない頻度でしかブラフを打っていないのは何故か。
この疑問❶対しては、重要事項④に基づいて下記のような説明を与えることができそうです。
説明❶
例えば、相手のバリューハンドの一部であるAA,KK,QQ,AK,KQはあなたのブラフキャッチャーの一部であるAQ,KJs等によってブロックされており、Vの値はそのブロックされているAA,KK,QQ,AK,KQ(及びこの例以外のブロックされているバリューハンド)を減らした後のコンボ数として計算する必要があり、それに伴ってBの値も低下するから。
【バリューブロックの例】

次に、疑問❷を再掲します。
疑問❷
あなたは、(公式2)から導出した値よりも少ない頻度でしかコールをしないのは何故か。
この疑問❷に対しては、重要事項⑥に基づいて下記のような説明を与えることができそうです。
説明❷
例えば、あなたのブラフキャッチャーの一部であるAQ,KJs,JTsは相手のブラフレンジの一部であるQJs,QTs等によってブロックされており、Cの値はそのブロックされているAQ,KJs,JTs(及びこの例以外のブロックされているブラフキャッチャー)を減らした後の全体コンボ数に対するコール頻度として計算されるべきものであり、そのブロッカーを考慮しない値よりも小さくなるから。
【ブラフブロックの例】

以上で見た通り、ブロッカーの存在は(公式1)及び(公式2)により算出される値を低下させるように働きます。従って、ベットやコールをする前にお互いのブロッカーをイメージする価値はありそうです。
注意編:大きいベットが損になるシチュエーション
ポラライズによる大きいベットが強いからと言って、シチュエーションを考慮せずに大きいベットするのは危険です。例えば、相手のハンドレンジにもナッツ級ハンドが存在し、且つ、簡単にフォールドできるゴミハンドがたくさんある時には、大きいベットはEVを大きくロスすることになり得ます。何故なら、ベット額が大きいほど(公式2)から算出される相手のコール頻度Cは小さくてよく、従って、相手は低頻度で存在するナッツハンドのみで+EVのコールをすれば十分となり得るからです。
おわりに
以上で見た通り、ポラライズドレンジがコンデンスドレンジに対して発揮する優位性は数学的に裏付けられています。一方で、「強いハンドを持っている時は相手にコールして欲しいから小さくベットする!」という初級者の方はとても多いです。そして、ポラライゼーションアドバンテージがある時にそのようなベットをすることはとてももったいないことです。ポラライズを活かしてEVを最大化し、勝ち組を目指しましょう!
(とは言え、本記事で扱った内容は理論的な側面が大きく実戦にそのまま活かすことのできるような内容ではないので、solverの結果を理解するための基礎知識として活用いただけると幸いです。)
