
トナメ虎の巻 ~ICMとBubble Factor~
現在、日本でポーカーをプレイする際は基本的にトーナメントが中心。そんな環境において、ICMやBubble Factorなど、トナメで重要なトピックについてはぜひ理解しておきたいところ。
ところが、なかなかそれらについて踏み込んだ発信は少なく、JOPTなどの大型大会では頻繁に「この人ICMやBubble Factorを理解してないな」と思う場面に遭遇します。というかICMやBubble Factorを理解していそうな人に出会う機会がほとんどないくらいです。国内の有名なポーカープレイヤーですら、それらを理解していなさそうな発言をしているのを目にすることもよくあります。
その原因ですが、見当はついています。
「ICMって難しそう(だから勉強したくない)」
僕も最初はそんな感じでした。
ただ、ICMのコンセプト自体はそこまで難しいものではなく、一度理解すればずっと使える知識なので簡単に内容をかみ砕いて説明してみます。
この記事を読むことで以下のような疑問を解消できればと思っています。
ICMってなに?どう役立つの?
Bubble FactorとかRisk Premiumってなに?
実戦のアクションでどう活かせばいいの?
今回はあくまでICMの導入と活用イメージを紹介する程度(それでも文字数多めですが)にとどまるため、必ずしも明日からすぐに使える知識や戦略が身に付くわけではありません。しかし今後皆さんの経験値がたまり、自分でICMに基づく分析をする場合には必ず使うことになる基礎知識となるので、わからなくなったり忘れたりした場合は繰り返しこの記事に読んでみてください。
1. ICMを知る

ICMとは?
ICMはIndependent Chip Modelの略称で、トーナメントにおけるチップの量を金銭的価値に変換する数式モデルです。

トーナメントの賞金ストラクチャー
残存する全プレイヤーのチップ量
をICMにインプットすることで、各プレイヤーの持つ賞金期待値を算出することができます。
これはトナメプレイ中に暗算で算出できるほどシンプルな四則演算ではないため、通常はICMIZERやHRC(Holdem Resources Calculator)と呼ばれるソフトを用いて計算します。
本記事では細かい計算は割愛しますが、興味のある方は以下の記事を読んでみると概要をつかむことができると思います。
トナメの戦略について語られる文献では頻繁に「ChipEV」「$EV」という単語が出てきますが、それらの定義は以下の通りです。
ChipEV…チップの価値=金銭的価値となるときの期待値
$EV…チップの価値をICMで金銭的価値に変換したときの期待値
ChipEVはICM適用前の期待値で、$EVはICM適用後の期待値、と考えることができます。
キャッシュゲームで扱う期待値はChipEVに該当するため、キャッシュを専門に取り組んでいるプレイヤーはChipEV脳になっています。そのためトナメでプレイする際は$EV脳に切り替える必要があります。
ICMを導入する理由
キャッシュゲームではチップが現金価値を持っているため、特定額のチップを獲得することで得られる価値と、チップを失うことで損なわれる価値は等価です。
100ドル分のチップを獲得→100ドルの収入
100ドル分のチップを喪失→100ドルの損失
トーナメントでは、参加費を支払った瞬間に特定の量のチップを渡されますが、そのチップがいくらの価値を持っているかはよくわかりません。参加費と同額の価値を持っている、と勘違いする人もいますが、厳密にはそこから運営費用や手数料として10〜15%分が差し引かれて賞金分配されるので、参加費とは一致しません。
また、トナメが進行して何人かが敗退して人数が減ると賞金を獲得できる確率は向上するので、中盤~終盤では参加費以上の価値になっているかもしれません。
それを計算する方法が前述のICMです。ICMによって自分の持っているチップの価値を算出することができます。
…ん?それって意味あるの?
今自分が持っているチップの価値を計算できたところで、その情報だけでは何の役にも立ちません。自分の賞金期待値が1ドルだろうが1000ドルだろうが、その数値単体でアクションを決めることはできないからです。
そこで、持っているチップ量を変化させてみます。
例えば、インマネまで残り10人のところでAさんが10,000チップを持っていたとしましょう。全プレイヤーのチップ量と賞金ストラクチャーをソフトに打ち込んで計算してみると、自分の10,000チップには1,000ドルの価値があることが分かりました。
10,000チップの価値=$1,000
その後、AさんがテーブルチップリのBさんとオールイン対決となり、その戦いに敗れてチップがゼロになったときの賞金期待値を考えてみます。これは計算ソフトを利用する必要すらありません。インマネせずに敗退したので、期待値はゼロです。
0チップの価値=$0
次に、AさんがBさんとのオールインを制し、ダブルアップに成功して10,000→20,000へとチップが増えたときの賞金期待値を考えてみます。このときの20,000チップの価値をソフトに打ち込んで計算してみると1,800ドルの価値があると判明したとします。
20,000チップの価値=$1,800
これを踏まえると、ある時点において10,000チップを持っているとき、
10,000チップを獲得→$800ドルの$EV増加
10,000チップを喪失→$1,000ドルの$EV減少
となっていることになります。
つまり全く同じ10,000チップの増減でも
チップ獲得時の$EV増加<チップ喪失時の$EV減少
となっています。
上記はあくまで一例ですが、基本的に複数人に賞金が分配される形式のトーナメントにおいては、正確に計算すると必ず↑の不等式が成立します。
つまり、トナメではチップを減らしたときのダメージがデカくなるということです。
これこそ、トーナメントという仕組みがポーカーに与える歪みです。ICMを使うとこの歪みを計測することができます。
ICMを導入する意義は現在持っているチップの価値を知ることではなく、チップの増減と賞金期待値の増減の非対称性=歪みを捉えることにあります。
その「歪み」を数値化した指標…それがBubble Factor/Risk Premiumです。ICMはこの2つの指標を計算するための道具に過ぎません。次章でBubble Factor/Risk Premiumについて見ていきます。
ポイントまとめ
ICM…トナメのチップの価値を金銭的価値に変換する数式
ChipEV…チップの価値=金銭的価値としたときの期待値
$EV…チップの価値をICMで金銭的価値に変換した後の期待値
トナメでは
「 チップ増加時の$EV+ < チップ減少時の$EV- 」
という歪みが生じるその歪みを数値化した指標をBubble Factorという
2. Bubble Factor / Risk Premiumを知る

Bubble Factorとは?
Bubble Factor(略称: BF)はICMの議論で必ずと言っていいほど出てくる単語ですが、その正確な意味を理解している人は多くありません。
しかし、その計算式は至って簡単です。
$$
BF=\frac{負けた時に失う\$EV}{勝った時に獲得する\$EV}
$$
前述記載の通り、↑は必ず分子>分母となるため、特殊な状況を除いて基本的にBF>1となります。一方でキャッシュゲームにおいてはチップ増減とEV増減は完全に一致するので、常にBF=1となります。
Bubble Factorはその名前からバブルラインでのみ発生するもの、と勘違いされがちですが、トナメ開始直後から最後のHUまでずっとBF>1で推移します。
参考)色々なトナメのBF
BFはトナメの形式や設計次第で大きく異なります。
参考までに特殊なトナメについて列挙します。
<勝者総取りトナメ>
賞金が1位にしか出ない場合BF=1となります。
その理由は簡単で、ICMでは
「賞金期待値=1位の賞金額 x 自チップ/総チップ」
と計算するため、チップ量が10%増加すれば賞金期待値も10%増加しますし、チップ量が10%減少すれば賞金期待値は10%減少します。
この形式のトナメのことを、英語では"Winner Takes All(ウィナーテイクスオール)"と呼んだりもします。
<Heads Upトナメ>
Heads Upトナメも勝者総取りと同様BF=1となります。自分のチップ量と相手のチップ量の割合がそのまま勝率に等しいと仮定すると、
「賞金期待値=勝利時Prize up x 自チップ/総チップ」
となります。
要するにHUトナメは相手を変えながら何度も1vs1の勝者総取りトナメを繰り返す形式のトナメ、と考えると分かりやすいかもしれません。
<サテライトトナメ>
サテライトトナメは参加人数の上位数%のプレイヤーに本戦出場権利を付与する、という予選形式のトナメです。
通常サテライトの出場料は本戦に直接出場するよりも割安になっており、その出場料の差分(本戦出場料ーサテ出場料)が実質的なプライズになります。
このトナメでは等価値のプライズが複数人に配られるため、たとえば上位5人に権利が付与される条件だと、6人目が飛んで時点で1位であることと5位であることの価値が等価になります。
つまり、
・1位でトナメを終えるインセンティブがない
・5位に入るvs6位で飛ぶ の価値差分がとても大きい
ということになります。
1位から順に賞金傾斜がかかるような一般的なトナメと比較して、サテライトトナメのバブルラインでのBFはかなり大きくなるのが特徴です。
ここで一つ、とても重要な注意点があります。BFは絶対的な指標ではなく、相対的な指標である、ということです。
意味が分からないと思うので言い換えます。BFは自分一人のチップ量で決まるものではなく、戦う相手次第で変化する、ということです。
自分がテーブル内で中くらいのチップ量を持っているとき、対戦相手がテーブルチップリなのか、数bbしか持っていないショートなのか、でBFは全く異なります。当然それによって戦略も大きく変わります(後述)。
Risk Premiumとは?
Risk Premium(略称: RP)は、BFとセットで出てくる指標です。この指標はBFを実戦用に変換した指標という感じです。
$$
RP=\frac{BF}{BF+1} - 50\%
$$
この指標の意味、使い方を簡単に説明します。
まず、このRPはBFが高い=期待値の歪んだ状況における必要勝率を求めるための指標、と考えると分かりやすいです。
キャッシュゲームなどBFが全くない状況では
チップ獲得時のEV増加 = チップ喪失時のEV減少
となる(BF=1)ため、デッドマネーがない時の期待値がプラスになるかマイナスになるかの境目、損益分岐点となる勝率は50%で、RP=0です。
$$
RP=\frac{1}{1+1} - 50\%=0\%
$$
しかし、トナメの特に中盤~終盤など、BFが高くなっている状況ではチップ減少時のダメージが増しており、50% : 50%の勝率では期待値マイナスとなってしまいます。つまり、ブレイクイーブンとなる勝率を導出するための補正が必要となります。その補正の度合いこそがRPです。
前述のAさんの例でBFとRPを計算してみましょう。
10,000チップを獲得→$800ドルの期待値増加
10,000チップを喪失→$1,000ドルの期待値減少
これをもとにBFを計算してみます。
$$
\begin{align*}
BF&=\frac{負けた時に失う\$EV}{勝った時に獲得する\$EV}\\
&=\frac{1000}{800}\\
&=1.25
\end{align*}
$$
ここから、RPを計算します。
$$
\begin{align*}
RP&=\frac{BF}{BF+1} - 50\%\\
&=\frac{1.25}{1.25+1} - 50\%\\
&=55.5\%-50\%\\
&=+5.5\%
\end{align*}
$$
つまり、Aさんがオールイン対決に直面しているとき、ChipEVで計算される必要勝率50%に+5.5%を補正した55.5%の勝率を基準としてアクションを決定しなければならないことがわかります。BFの数値が高くなると、当然ながらRPの数値も高くなります。
ゴチャゴチャ式を書きましたが、この計算からわかることを簡潔に言います。
「BFが高い状況では、オールイン対決での必要勝率が上がり、特にオールインに対するコールレンジを狭くする必要がある。」
計算式はこの際忘れてもいいです。まずは↑だけ覚えましょう。
キャッシュとトナメの大きな違いとなるのはこの部分です。僕自身、キャッシュゲームからポーカーを知ったたため、この感覚に慣れるのに時間がかかりましたが、再現性高くトナメで成績を残すためには欠かせない知識です。
参考情報として、目安となるBFおよびRPの水準をまとめておきます。

特に重要になってくるのはBFが1.5を超えるような状況です。この場合は相手のレンジに対する必要勝率が60%となるため、こちらのcallレンジをかなりシビアに選定する必要が出てきます。
※ 高BF下でのオープンレンジ / ディフェンスレンジ
「オールインに対するコールレンジが狭くなる」と書きましたが、オープン頻度やオープンに対するBBのコール頻度はBFが高くなっても大きな差がないことには注意が必要です。ただし、そのレンジ(ハンド)の内訳は変化するため、その特徴を覚えることは有益です。そちらは別記事でまとめたいと思います。
※ 高BF下でのオールインレンジ
「オールインに対するコールレンジが狭くなる」と書きましたが、オープンオールイン / 3betオールイン / 4betオールイン のレンジはそれぞれ異なる動き方をします。こちらもオープン / ディフェンスレンジと同様に別記事でまとめたいと思います。
ポイントまとめ
ICMを用いることでBFを計算することができる
BFは「対峙するプレイヤーが誰か?」で変化する
BFは基本的に1以上の数値となる
BFを用いることでRPと必要勝率を計算することができる
BFが高い状況ではオールインコールレンジを狭くする必要がある
3. BFが高くなるタイミングを見極める
前章までで、トーナメントでは期待値が歪み、その歪みをBubble Factorとして計算可能であることを確認しました。
それではその歪みが大きくなる=BFが高くなるのはいつでしょうか?それを視覚的に確認してみます。
トナメ中のBFの推移
以下の図はとても大事な図なので目と心に焼き付けてください。

縦軸:プレイヤーの平均BF
横軸:残りプレイヤーの人数
としてグラフを描画したものです(横軸は対数)。
これは「Kill Everyone(2009)」という書籍で紹介されているもので、10,000人参加のSunday MillionsというオンライントナメにおけるBFを計測して作成されたものです。
当然賞金構造やプレイヤーのスタック状況によって多少変化はありますが、どのトナメでも概ねこの図のような推移をすると考えて問題ないです。
この図を見ながら、トナメ中の平均BFの推移を確認していきましょう。
★Start ~ ITM Bubble (10,000→1,500人)

トーナメント開始直後からインマネバブルにかけて、BFはジワジワ上がっていきます。このトナメもそうですが、海外トナメやオンライントナメの大半は参加人数の15%前後がインマネのラインとなるケースが多いため、まずは上位15%に残ることを目指すことになります。
序盤はChipEV(≒キャッシュ)に近い戦略でプレイして問題ないと言えますが、スタート直後はEffective Stackが深く、そもそもオールインになるケースがそこまで多くないでしょう。
問題はそこから時間が経過し、バブルに近づいている時です。残り人数が30%くらいになると徐々にBFが上昇し、1.3を超え始めます。そしてバブル直前にBFの上昇はピークに到達し、1.5を超えます。このあたりでは、BFを意識したプレイをすることが推奨されます。
バブルが弾けると、その瞬間にBFが急落します。そうなるとチップ喪失による$EVロスが一気に小さくなるので、そこそこ広くショートのオールインを受けられるようになります。
★ITM Bubble ~ 3Table(1,500→30人)
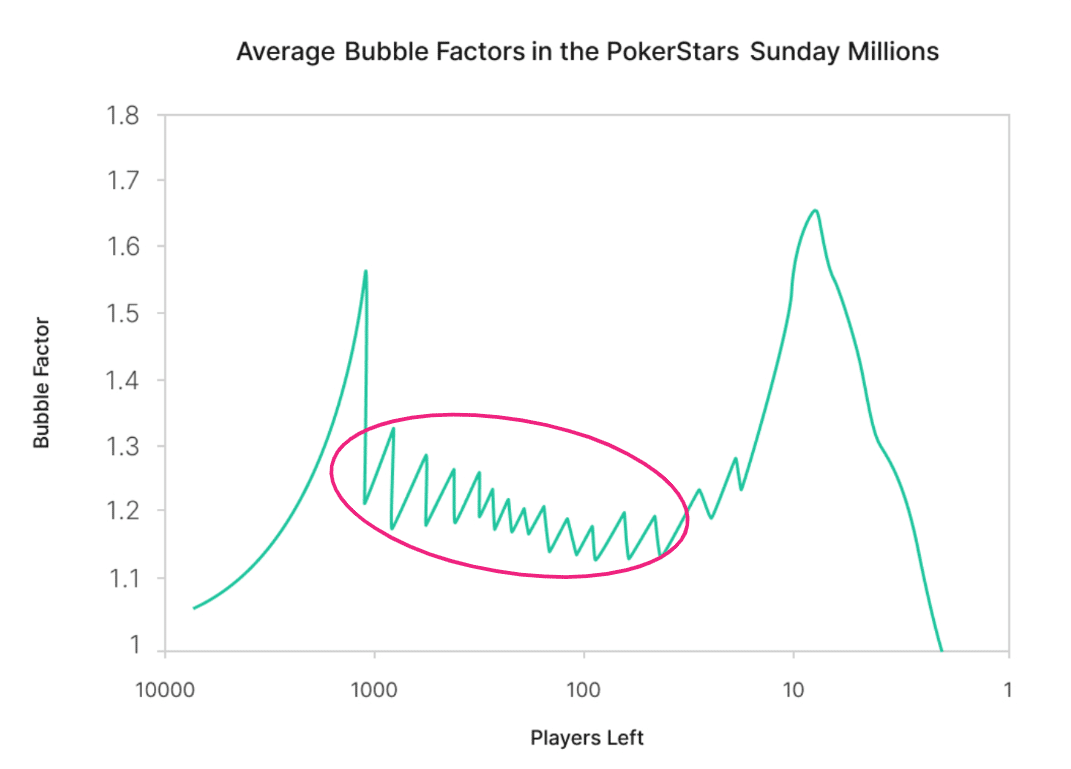
バブルが弾けた後はしばらくBFが低い状態が続きます。ギザギザした形をしているのはプライズジャンプに相当する部分です。プライズジャンプが近づくとBFは若干上昇し、ジャンプ直後は下降しますが、プライズジャンプ額が相対的に小さいこともあってその上昇幅は限定的です。

ここからしばらくはチップ喪失による$EVロスが小さい状態が続きます。
★3Table ~ Final Table(30→10人)

残り30人になると上位のプライズジャンプの影響が相対的に大きくなってBFが上昇し、残り10人あたりで再度ピークを迎えます。
↑の例のSunday Millionsもそうですが、ライブトナメも基本的にはトップヘビーなストラクチャーとなっており、バブル後に再びBFが大きく上昇していくのは上位1%を切ったくらいのタイミングです。


このタイミングではインマネバブル付近と同じかそれ以上のBFがかかるため、より慎重な立ち回りが必要になります。
★Final Table~Heads Up(10→2人)

FT後は、HUに近づくにつれてBFが減少していき、HUになった瞬間BF=1となります。つまり、トナメ開始直後やキャッシュゲームと同様にChipEVでプレイすることとなり、歪みがなくなっています。
以上トナメの進行に伴うBFの変化をまとめます。
残り人数30%くらいから徐々にBFが上昇し始める
バブルラインでBFは最初のピークを迎える
バブルが弾けてITMが決まるとBFは急落する
その後はプライズジャンプ毎に上下動を繰り返す
残り人数1%を切った辺りでBFは再度上昇する
FT付近でBFの上昇は二度目のピークを迎える
FT後はプレイヤーが飛ぶ毎にBFも減少し、HUで1になる
この流れを先程のグラフとともに頭に入れておくと良さそうです。
スタック状況とBFの関係
前項でトナメの進行に伴ってBFがどう変化するかを確認しましたが、そのBFはあくまで全プレイヤーの平均値でした。僕たちプレイヤーが検討すべきことは「現在の自分のBFはどれくらいか」であり、そこに影響を与える最も重要な要素はテーブル内のチップ量の分布です。
細かく分類するとキリがないので、ここでは大まかな傾向を見てみます。
★自分がチップリーダーのとき

自分がチップリーダーのときはBFは低くなります。仮にショートスタックとのオールイン対決に負けたとしても相手をカバーしている限り飛ぶ危険性はなく、依然としてチップ量が多い状況を維持できるため、チップの喪失による$EV減少はそこまで大きくなりません。
ただし、相手がミドルスタックやビッグスタックであれば、自分がチップをカバーしていることを考慮しても、大きなポットを落としたときのダメージはかなり大きくなってしまうため、注意が必要です。
★自分がショートスタックのとき

自分がショートスタックのときもBFは比較的低くなる傾向があります。ショートスタックはそもそも保有している$EVが低く、飛べば$EVはゼロになる一方で、仮にダブルアップしたとしても飛ぶ危険からは解放されず、大きな$EV改善が見込めないことから、チップの増減と$EVの増減の歪みが小さくなる傾向にあります。
ショートスタックは失うものも得るものも少ないためBFの影響をあまり受けない、と言えるでしょう。
★自分がミドルスタックのとき

自分がミドルスタックのときはBFが高くなります。これがICMを学ぶ上で最も重要なポイントといっても過言ではありません。自分以外にショートスタックがおりインマネの確率がそこそこ高い状況で、そのショート達を差し置いて飛んでしまうのはとても大きな$EVロスとなってしまう一方、チップをダブルアップさせてもそこまで大きく$EVの向上は期待できない、という中途半端な位置にいることが原因です。
失うものは大きく得られるものはあまりない状態と言えます。
JOPTでも何でもいいです。トナメ終盤のあと少しでインマネ / 権利獲得というときにミドルスタック同士でぶつかり、他に多くのショートスタックがいるのを理解しているにも関わらず、Riverの相手のオールインに「トップヒット降りられないよ~」と言ってcallして敗退したことはありませんか?その瞬間、とんでもない期待値ロスをしていたかもしれません。
★スタック状況まとめ

以上の情報をまとめると、自分がチップリーダーのときは比較的リスクを許容することができるため、チップを失いたくないミドルスタックをいじめることで通常よりも多くfoldEQを得ることが可能です。逆に言えば、それまで慎重にプレイしていたミドルスタックが強いアクションで抵抗してきたときは相手のレンジがかなり強くなっていると言えます。
また、自分がショートスタックになってしまったときは、BFはそこまで高くないため相手を選ばずにプレイすることは可能なものの、わざわざダメージの少ないチップリに突撃するよりも、オールインに敗れると自分と入れ替わってショートに転落してしまうようなスタックの少ないプレイヤーに勝負を挑むほうが期待値は(自分よりショートが生まれるため)高くなり、相手にもプレッシャーをかけることができます。
最後に、自分がミドルスタックのときはチップリーダーや同程度のスタックと大きなポットを争うのは期待値的に好ましくありません。オールイン対決に敗れてもまだ戦えるようなショートスタックとの戦いを基本線としつつ、やむを得ずミドルスタック以上との戦いに巻き込まれたときはぶつかり合いは避け、ナッツ級で対抗できるタイミングを我慢強く待つ、という形で立ち回ることが必要です。
※ $EVロスはどこへ行く?
ミドルスタック同士がぶつかった場合、ショウダウンされるまではお互いの$EVが削られるため、双方の$EVの合計はハンドが配られる前よりも小さくなります。
しかし、ポットレーキのないトナメでは全プレイヤーの$EV合計が賞金総額と一致し続けるはずなので、上記は違和感のある結果に思えます。ぶつかりあっている2人の$EVが失われるなら、他の誰かが$EVプラスになっていないと辻褄が合いません。
ではミドルスタック同士が戦った時の$EVマイナスはどこに行くのでしょうか?
それは…2人よりショートなプレイヤー全員です
なんと、ミドルスタック同士が3bet/4betなどとポットを膨らませるたびに、既にフォールドしてその様子を傍観している全てのショートスタックプレイヤーたちに$EVが降り注いでいくのです。
自分がそのぶつかり合いの当事者なのであれば、指をくわえて見ているショートスタックたちに$EVを配るようなプレイをする以上、それに見合うだけの十分な勝率が求められるのは当然です。
ミドルスタック同士でぶつかり、フラッシュドローでセミブラフのx/rを検討しているその瞬間、あなたはポットを争っているプレイヤーだけではなく、安全なところから口を開けて$EVが降り注ぐのを待っているショートスタックたちについても考慮する必要があるのです。
ポイントまとめ
トナメ進行においては、インマネバブルとFT付近でBFはピークを迎える。
スタック状況としては、ミドルスタックのプレイヤーが特に高いBFを持つことになる。
トナメの進行とテーブルのチップ状況から、どのプレイヤーがどんなBFを持っているか、を脳内でイメージし、相手次第で戦略を変えることが重要になる。
4. 実戦での事例
Bubble Factorが高いときは、キャッシュゲームとは異なるプレイラインを取る必要があることを説明してきました。
それでは、実戦ではそのプレイラインはどのくらい変化するのでしょうか?例を挙げて見てみます。
トナメ概要
今回ピックアップするのは2023年の夏にモナコのモンテカルロで開催されたEPT Super High Roller(参加費: €100,000≒約1500万円)のFinal Tableです。

この超高額トナメには世界中から37名の鉄強プレイヤーが参加し、賞金は6位から割り当てられました。

この時点で残りは7人となっており、まさにバブルライン真っ只中という状況です。
テーブルのスタック状況
テーブルのスタックは、アベレージスタックが22bbという状況の中でMikita BadziakouskiとAlex Kulevという2人のプレイヤーが40bb以上の飛び抜けたチップを持っており、残りの5人が10~20bbくらいで固まっている状況です。

インマネすれば3,800万円分の賞金を獲得でき、逆にここで飛んでしまうと何も得られないまま帰宅することになります。そんな状況で下位5人が団子状態と考えると、その5人のBFはかなり高い値となっていることが予想され、10bb前後のショートも簡単にはオールイン/オールインコールできる状況でないことは頭に入れておきます。
特徴的なスポットの考察
今回は、とあるスポットでのMikita BadziakouskiとBen Heathのハンド・アクションに注目してみます。
参考までに2人のプロフィールを紹介しておきます。

上記の通り、この2人は文字通り世界中のプロポーカープレイヤーの中でもTop of Topであり、ICMやBF/RPは当然理解していることが想定されます。
※ Ben Heathコワイ
余談ですが僕はEPT Paris 2023 Main EventのDay2でBen Heathと同卓しました。彼はショートで移動してきたかと思ったらあっという間にチップをモリモリ増やし、卓が割れる頃にはテーブルチップリになっていました。僕自身はチップを奪われなかったのですが、他のプロとの激しい打ち合いを目の当たりにして若干トラウマになっています。

このスポットでMikitaがBUです。COまでフォールド、BUのMikitaにアクションが回ってきました。
チップリであるKulevはCOでfoldしており、アクションが残っているBU/SB/BBの3人の中ではBUのMikitaが圧倒的にチップを持っています。
BUのMikitaのハンドはQ♥4♥。
ここで彼はオープンオールイン要求を選択します。

ここでSBのBen HeathにはAQoが。ハンドランクとしてはかなり上位に位置するハンドです。

Heathのスタック量は7人中4位と中位に位置しているためあまり無理をしたくはありませんが、Mikitaはこのスポット以外でも幾度となくチップ圧を活かしたオールイン要求をしており、ほぼエニハンでやっていることは自明なため、適切に抵抗したいところ。
タイムバンクを使い、最終的に彼が下した決断は…

なんとAQoをフォールドしました。
すぐ後ろにいたショートスタックのSuvarnaもBBを守らずスナップでフォールドし、結果的にMikitaがBlindとAnteをスチールしてこのスポットは終了しました。
ICM計算ソフトを用いた検証
では、実際にこのスポットでのBU=Mikita/SB=Heathのプレイを、ICM計算ソフトHoldem Resources Calculator(HRC)で計算してみます。

★BUのオープンオールインレンジ
MikitaはQ4sというそこまで強くないハンドでオールイン要求しましたが、実際にHRCで計算した結果は、なんとAA, KK, QQ, AKs, AQsなどのプレミアハンドおよびT2o-62oの一部を除いて、多くのハンドでオープンオールインとなりました。

BUが圧倒的に多くのチップを持っている
後ろの2人がチップが少ない
フォールドしたプレイヤーの中にSB/BBと同程度のショートスタックが2人いる
バブルラインでBubble Factorがとても高い
という要素が重なり、SB/BBのコールレンジが狭まるため、逆にそれを利用する形でBUのオールインレンジが極限まで拡大されています。
例えばこの状況で64oなどもオールインする、というのは一見すると勇気のいるアクションに感じるかもしれませんが、計算上はそれすら期待値プラスになるのがこのスポットの興味深いところです。
BFが高いときはレンジを絞る必要がある、と前述しましたが、逆に相手のBFが高く自分のBFがそこまで高くない場合は、相手のレンジが狭くなっていることを利用して、このように広いレンジでアグレッシブに戦うことが肯定されます。
★SBのコールレンジ
HeathはAQoというPreflop時点ではかなり強いハンドが配られたものの、BUからのオールインを受けて、悩んだ末にAQoをフォールドしました。その時の適正アクションを確認してみましょう。

なんと、AQoどころかAKoすらもフォールドという結果になりました。コールできるのはハイポケットとAKs, AQsのみ。一見降りすぎにも思えるこのアクションは、ICM計算上適正なアクションだったのです。
★なぜAQoはフォールド推奨なのか?
BUのほぼエニハンオールインに対して、AQoはフォールドになるのでしょうか。これを把握するため、まずはSBのBUに対するBubble Factorを確認します。

赤枠実線のSBのvsBUでのBubble Factorは2.42という極めて高い値となっており、Risk Premiumは+20.8%になります(逆に赤枠点線のBUのvsSBでのBubble Factorは1.24とかなり低い値になっていることもポイントです)。
SBにとってのChipEV上の必要勝率はAnte等も考慮すると15 ÷ 33 ≒ 45.5%のため、そこにRPを足した$EV換算後の必要勝率は 45.5%+20.8% ≒ 66%ということになります。
BUのほぼエニハンオールインに対するAQoの勝率をEQ Calculatorで調べてみると…

勝率65.2%でギリギリ必要勝率(66%)に届きません。
これが、AQsだった場合は…

今度は勝率67%となりギリギリ必要勝率(66%)を満たしています。このスポットにおいてはAQs/AQoが境界になっていたようです。
これがHUやキャッシュゲームであれば、AQoの勝率がChipEV上の必要勝率である45%を大きく上回っているため楽々コールできますが、トナメのバブルラインではこれほど適正アクションが大きく歪んでしまう、ということがわかる典型例といえます。
今回はキャッシュゲームをプレイする感覚と大きくズレるスポットをあえて選んで紹介しましたが、チップリならいつでもどこでもオールインしろ、ミドルスタックはなんでもかんでもタイトに降りろと言いたいわけではなく、あくまで相手と自身のBFを理解した上で適正なアクションを選択するプロセスの一例を提示しただけなので注意してください。
トナメをプレイしていると必ずシビアな判断が求められる場面が訪れます。その際にできるだけ期待値マイナスとなるプレイをしないためにも、相手と自分のBFを意識し、バブルライン含め様々な場面での立ち回りを理解することが重要です。
ちなみに、このトナメはチップリのMikitaとKulevの2人が最後まで残ってHUを戦うことになるのですが、ここでAQoをフォールドしたBen Heathは見事3位に入賞して約8,300万円の賞金を獲得しています。
★どうやってこのプレイを再現するのか
上記の通り、偶然か必然か海外の鉄強プレイヤーたちは適正なプレイをしていたことが検証できましたが、この計算を卓上で実行するのは不可能です。
では私たちはどのようにして彼らのようなプレイを目指せばいいでしょうか?これはあくまで僕の一意見に過ぎませんが、地道な実戦・検証を繰り返すことが最も重要だと考えています。
<検証イメージ>
トナメプレイ中にBF/RP/適正レンジについて脳内で仮説を立てながらアクションを決める

プレイ終了後、ツールを使用してその仮説と計算結果との誤差や理由を確認する

それまでの相手のShow Downから相手のレンジと適正レンジの誤差を見積もり、それに対するExploit余地がなかったかを検討する

トナメのさまざまなスポットでBubble Factorを実際にソフトで計算してみて、特定の場面・スタック状況でBF/RPはどんな値となるのか、オープン / 3bet / 4betレンジ・それぞれに対応するコールレンジはどう変化するのか、等を何度も検証し、「この状況だとBF=1.8/RP=+14%くらいだからレンジはこうなりそうだな」のようにBFやRPの感覚を研ぎ澄ませることで、ソフトを使用できない実戦でもプレイ精度を高めることができるでしょう。
また、トナメ開始前であれば自分で事前にBF/RPを計算することはルール上問題ないため、例えば翌日にFT進出が決まっている場合は前日までにいくつかのシナリオでソフトを回してBFや適正レンジを確認しておく、などは手っ取り早く再現性を高める方法の一つです。
便利な分析ツール
ICMを用いてBFやRPを計算する上で便利なツールを紹介しておきます。
まず最初にオススメするのは、本記事でも検証に利用したHRCです。このツールを使えば具体的なスポットをかなり細かく分析することができます(月額料金が数十ドルかかるのでお財布と相談してみてください)。
特徴としてはpush/foldだけでなく、2bb openやcold callなど、卓上で起きるさまざまなシチュエーションを考慮して計算することが可能です(計算速度もかなり速め)。いずれHRCの使い方や設定方法なども記事として紹介しようと思っています。
ただし、BBのcall / 3betなど一部のスポットでPost-flopのEQRが考慮されておらず精度が低い、という指摘もあるため、スポットによっては次に紹介するGTO WizardのICM Solutionと併用するのがオススメです。精度の高い分析をする場合は後述するSimple Preflopというツールも検討してみてください。
HRCは非常に便利ですが、賞金ストラクチャーと各プレイヤーのスタック量をインプットする必要があり、なんだかんだ手間のかかるツールです。
それに対して、特徴的ないくつかのシチュエーションをプリセットで用意してくれているのがGTO WizardのICM Solutionです。

いくつかの用意されたスタック分布の中から自分が調べたいスポットに近似したものを選ぶことで、おおまかなアクション傾向を調べることができます。その用意されたスポットにおける計算精度はとても高いので、かなり信頼できる戦略となっています。
UIもわかりやすくインプットも不要なため、普段はHRCよりもこちらをヘビーユーズしています。
月額料金がかかりますが、集合分析やレンジドリルなど用途も多岐にわたるので、かなり満足度の高いツールです。
先ほどのHRCよりも計算精度という点で上回っているとされるツールがSimple Preflopです。こちらは計算処理に時間がかかりPCスペックを要するものの、かなり細かい条件設定が可能であり、ポストフロップから逆算される期待値を正確に計算をしてくれるので、上級者向けのツールとしては最適かもしれません。HRCやGTO Wizardだけでは物足りない方はぜひこちらの利用も検討してみてください。
最後に紹介するのはICMIZERです。このツールも非常に有名ですが、push/fold/callのレンジ確認がメインとなっており、2bb openやcold callなどの細かいアクション分岐を設定できなかったので、正直HRCでこと足りるのではないかと思っています(すでにアップデートされているかもですが)。
5. まとめ
ここまで、ICM/BF/RPのキホンのキについてまとめてみました。キャッシュゲームとトーナメントだと、その仕組みによって大きくゲーム性が変化することが確認できたかと思います。
一番のポイントは、トーナメントではキャッシュゲームと違ってハンドを配られる前に考えるべき変数が多い、ということです。
トーナメント形式
賞金ストラクチャー
残り人数
テーブルのスタック分布
各プレイヤーのスキル・ICM理解度
意思決定をするための多くのファクターが存在し、「自分のハンドの強さ」はその一部を構成するに過ぎません。
そうなると重要なのは、トナメに参加中に得られる情報(ブラインド・残り人数・アベレージスタック・同卓者のスタック量…etc.)をいかに正確に/即時に収集できるか、ということになります。
はじめからすべてを網羅することは難しいかもしれないので、まずは近くのアミューズなどで色々な情報を意識し、把握する練習をするといいかもしれません。
※ ICMの不完全性
本記事ではICMについてたっぷり語りましたが、ICMも完璧なモデルではないことが指摘されています。ICMでは以下の要素が考慮されていません。
・ポジション
・ブラインド/アンティ
・トナメ進行にともなうブラインド上昇
・各プレイヤーのスキル差分
こういった要素はHRCなどの計算ソフトでも考慮しきれない部分もあるため、ある程度自らで補完して仮説を立てる必要があります。とはいえ、何も確立された戦略モデルがなかった時代からすればICMが画期的なモデルであることに疑いはなく、当面はこのモデルで期待値を高めることを目指すのがよさそう、というのが現状の僕の見解です。
一方で、ICMに代わる新しいモデルもすでに開発・検証され始めているため、そういったモデルについても今後紹介できればと考えています。
最後に本記事の重要ポイントをまとめておきます。

本記事ではあくまで導入として限定的なスポットしか紹介できませんでしたが、必ずしも「ミドルスタックは超タイトにプレイしなきゃダメ」とか「チップリなら暴れまくって大丈夫」みたいな印象を与えたかった訳ではありません。今回はたまたまエニハンオールインとそれに対するコール/フォールドの判断を対象としましたが、例えばミドルスタックでも2bbオープンの頻度はそこまで低下しないし、チップリでもポジションや前後のアクション次第でタイトにフォールドすべきスポットも存在します。
そこで、今後は様々なシチュエーションでの立ち回りを検証・紹介できればと思います。
トーナメントの戦略を中心にしつつポーカーに関する情報の発信をしていく予定なので、気になる方はXおよびnoteのフォローをお願いします!
◆著者(Gaku) X
https://x.com/gaku_btn
また、直近でポーカー(主にトナメ)に関する知識・戦略の共有場所として「Scholar(スカラー)」というコミュニティを立ち上げました。僕自身は基本的にこんな感じで海外のコンテンツをまとめてnoteやYouTubeなどでの発信をメインで担当していく予定で、以下のDiscordでもう少し細かい話をすると思うので、興味がある方は入ってみてください💡
◆Scholar Discord
https://discord.gg/n5MS6qBk8Q
◆Scholar X
https://x.com/pokerscholar_
もしこの記事が参考になった!と思ったら、ぜひRTしたり、周りの友人や知人に薦めたりしてほしいです。WSOPやEPTで日本のプレイヤーが優勝する確率が1%でも増えるなら、それが僕の本望です。
