離散数学について
離散数学(Discrete Mathematics)は、個別の要素や離散的な構造を扱う数学の分野です。「離散」とは、連続していない、個別の要素を指します。例えば、整数やグラフの頂点のように、数えられるものや区切られたものを扱います。
これに対して、連続的なものは「連続」と呼ばれ、例えば実数や曲線のように、途切れなく続くものを指します。
離散数学には多くの興味深いトピックがあります。以下にいくつか紹介しますね。
1. グラフ理論(Graph Theory)
グラフ理論は、頂点とそれを結ぶ辺からなるグラフを研究する分野です。例えば、ネットワークの最短経路問題や、ソーシャルネットワークの解析などに応用されます。グラフ理論の基本的な問題として、オイラー路やハミルトン路の存在が挙げられます。
オイラー路は、グラフのすべての辺を一度だけ通る道のことを指します。オイラー路が存在するための条件として、無向グラフではすべての頂点の次数が偶数であるか、またはちょうど2つの頂点の次数が奇数であることが必要です。

ハミルトン路は、グラフのすべての頂点を一度だけ通る道のことを指します。ハミルトン路の存在を判定するための一般的なアルゴリズムは存在しないため、問題の難易度は高いとされています。

グラフ理論はまた、彩色問題やマッチング問題など、多くの興味深い問題を含んでいます。彩色問題では、隣接する頂点が異なる色になるようにグラフの頂点に色を割り当てる方法を探します。マッチング問題では、グラフの辺の集合の中で、共有する頂点を持たない辺の最大集合を見つけることが目標です。
2. 組合せ論(Combinatorics)
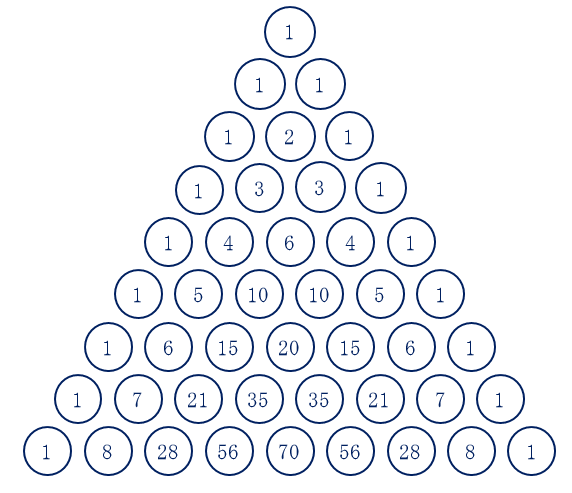
組合せ論は、物の配置や選び方に関する数学です。例えば、特定の条件を満たす組み合わせの数を数える問題や、パズルの解法などが含まれます。パスカルの三角形や二項定理などが基本的な概念です。
パスカルの三角形は、数の並び方を三角形の形にしたもので、各行の数は特定のルールに従って計算されます。このルールは、二項定理という数学の公式に基づいています。二項定理は、二つの項を含む式を展開する方法を示しており、組合せ論の基本的な道具の一つです。
さらに、組合せ論には順列や組み合わせといった概念も含まれます。順列は、物の並べ方の総数を求める問題であり、組み合わせは、物の選び方の総数を求める問題です。これらの概念は、確率論や統計学、暗号理論など、さまざまな分野で重要な役割を果たしています。
3. 計算理論(Theory of Computation)
計算理論は、計算可能性や計算の効率性を研究する分野です。チューリングマシンやオートマトンなどのモデルを用いて、どのような問題が計算可能であるか、またその計算にどれだけの時間や空間が必要かを分析します。
チューリングマシンは、理論的な計算モデルであり、任意の計算問題を解くための抽象的な機械です。これにより、計算可能な問題と計算不可能な問題を区別することができます。
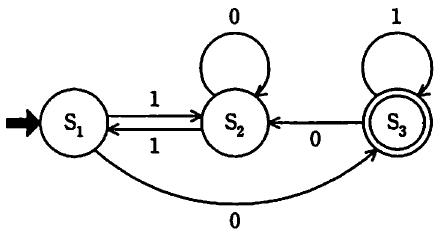
オートマトンは、状態遷移を通じて入力を処理するモデルで、正規言語や文法の解析に用いられます。これらのモデルを使って、アルゴリズムの効率性や計算資源の使用量を評価することができます。
計算理論はまた、NP完全問題やP対NP問題など、計算の複雑性に関する重要な問題も扱います。これらの問題は、計算理論の中でも特に難解であり、解決されていないものも多く存在します。
4. 符号理論(Code Theory)
符号理論は、データの誤り検出や訂正を行うための符号化方法を研究する分野です。例えば、デジタル通信やデータストレージにおいて、データの信頼性を確保するために使用されます。ハミング符号やリード・ソロモン符号が代表的な符号です。
ハミング符号は、データの誤りを検出し、訂正するための初期の方法の一つで、特に単一ビットの誤り訂正に優れています。一方、リード・ソロモン符号は、複数のビットの誤りを訂正する能力があり、CDやDVD、QRコードなどのデータストレージや通信システムで広く使用されています。
これらの符号化技術は、データの送信中に発生するノイズやエラーを効果的に処理し、受信側で正確なデータを再構築することを可能にします。符号理論の発展により、現代の情報通信技術はますます信頼性が高まり、効率的になっています。
5. 数論(Number Theory)
数論は、整数の性質を研究する分野です。特に、素数や合同式、ディオファントス方程式などが主要なテーマです。RSA暗号のように、現代の暗号技術にも応用されています。
合同式は、整数の間の関係を表すもので、数論の基本的なツールの一つです。ディオファントス方程式は、整数解を持つ多項式方程式の研究を指し、古代から現代に至るまで多くの数学者が取り組んできました。これらの方程式は、整数の性質を深く理解するための鍵となります。

数論の応用は、暗号技術にとどまらず、コンピュータサイエンス、情報理論、さらには物理学や生物学などの他の科学分野にも広がっています。例えば、楕円曲線暗号は、数論の一分野である楕円曲線の性質を利用しており、RSA暗号に代わる次世代の暗号技術として注目されています。
これらのトピックは、離散数学の広範な応用範囲を示しており、それぞれが独自の魅力と重要性を持っています。興味がある分野についてさらに調べてみると、新しい発見があるかもしれません!
by Copilot
