
同心円上を異なる速さで回る歯車
あるプロジェクトでタイトル通りのものを製作する必要が生じました。
下の図のようなイメージです。同じ点を中心に2つの歯車が同じ方向に回るのですが、回る速度が違います。この速度の比を特定の比にしたいのです。例えばこの比を 1:12 にすれば時計の短針と長針のような動きになります。

最終的にレーザー加工機やCNCルーターで切り出すための歯車のデータは Fusion 360で作ることができます。例えば以下の記事に詳しく書かれています。
簡単に言うと、歯車のサイズを指定すれば自動的に歯車の図形に変換してくれるという優れものです。
では、回転速度の異なる歯車の動きはどうすれば作れるでしょう。
シンプルには、大きさの異なる歯車を組み合わせればよいですね。

大きい歯車は小さい歯車よりゆっくり回ります。しかしこれだけだと問題点が2つあります。ひとつは同心円になっていないこと、もうひとつは回転の向きが逆になってしまうことです。
これを解決するには、以下のような歯車を考えます。


この図では、左右に2枚ずつの歯車が重なっており、左側の大小2枚の歯車は接着されていて同時に回りますが、右側の2枚(大きい方が手前で、裏に小さいのがある)は接着されておらず、異なる動きができるようになっています。このような歯車を作って右側の大きな赤い歯車を回すと、その動きが左側の黄色い歯車に伝わり、それと同時に裏のグレーの歯車が回り、それが右側の裏側にある歯車に伝わり、二段階で回転速度が変化します。
赤い歯車の歯の数をa、黄色い歯車の歯の数をbとすると、黄色は赤の b/a 倍の速度で回転することになります。同様にグレーの歯車の歯数をc、赤い歯車のうらにある歯車の歯数をdとすると、赤い歯車の裏にある歯車は、赤い歯車の b/a × d/c 倍の速度で回転することになります。ですので、赤い歯車とその裏にある歯車の回転数の比を所望の値にするには、そうなるようにうまく a, b, c, d の値を決めれば良いということになります。
しかし、それだけで a, b, c, d を決めてしまうと、下図のようになってしまうかもしれません。

これだと右側の歯車が同心円になりません。こうならないためには、黄色と赤の歯車の半径の和と、裏側に来るグレーとその右側の歯車の半径の和(青い2本の矢印の長さ)が等しくなるようにする必要があります。つまり a + b = c + d という条件を満たさなければなりません。
a, b, c, d は歯の数ですから整数でなければならず、そうなると欲しい回転数比を実現する a, b, c, d の組み合わせを探すのは結構大変になってきます。例えば時計の長針と短針を実現するのであれば、
(a, b, c, d) = (32, 8, 30, 10) とすれば
a/b × c/d = 12
a + b = c + d = 40 となり、うまく回転速度比 12倍を実現できますが、「回転速度比 1.23 を実現したい」などと任意の比を実現しようとすると適切な組み合わせを探すのが大変ですし、どんどん歯の数が大きくなっていき、現実的に作るのが難しくなっていきます。(ちなみに 1.23 の場合は (63, 75, 82, 56) で実現できます。)
さて、ここまで読んでこられる間に気づかれたかもしれません。「歯車の歯の大きさを変えたらいいんじゃない?」と。
そう気づいた方は鋭いです。2つの噛み合う歯車の組み合わせでは、両者の歯の大きさは同じでなければなりません。そうでないと回りません。ですので、上記であれば a と b、c と d の歯車の歯の大きさは同じでなければなりませんが、a と c の歯の大きさは同じである必要はありません。
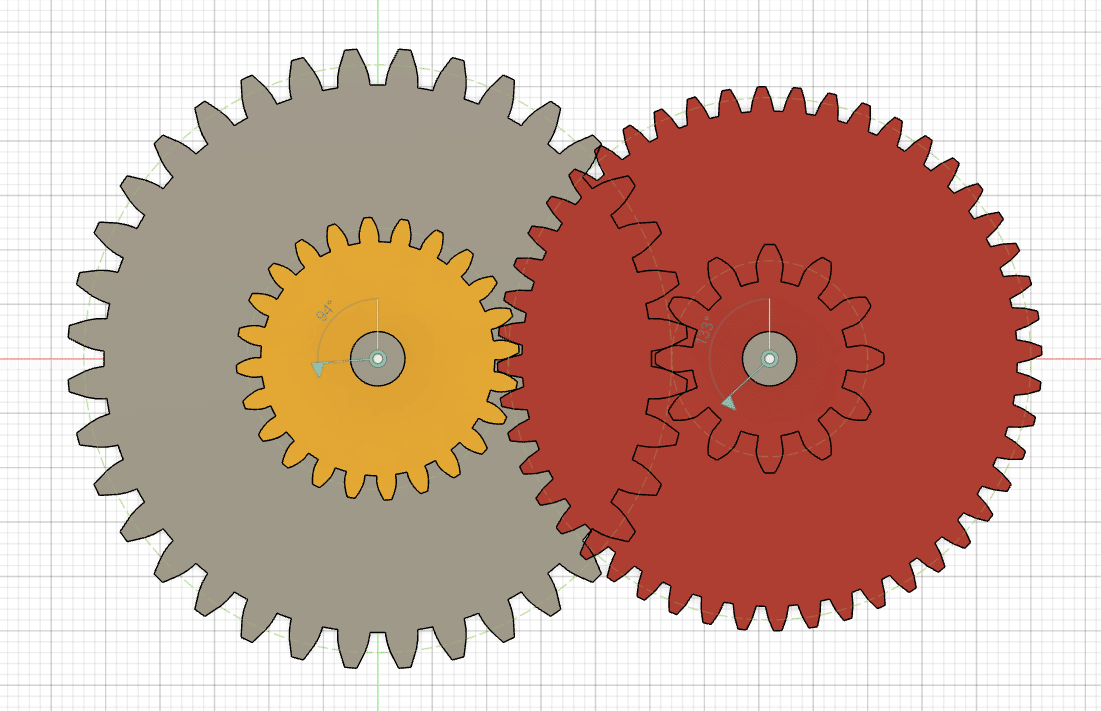
上の図は、前述でうまく行かなかった例と同じ歯の数ですが、グレーとその右の歯車の歯の大きさを大きくして右側の歯車がピッタリ同心円になっています。
実は(冒頭で紹介した記事にも書かれていますが)歯車を作図する際には、以下の2つのパラメータがあります。
・歯数 (N)
・モジュール値 (M)
モジュール値というのは、歯の大きさを示す値で、これを大きくすると歯が大きくなり、歯車の直径も比例して大きくなります。上記の例では、最初にモジュール値をすべて同じにして作図してみたら同心円にならず、青い2本の矢印が1.5倍違ってしまいましたので、グレーとその隣の歯車のモジュール値を1.5倍にすることでピッタリ合わせることができました。
というわけで、
a/b × c/d が欲しい値になるような整数の組 (a, b, c, d)を決める。
a + b と c + d を計算し、それが一致しなければ (a, b) か (c, d) いずれかのモジュール値を調整することで同心円状に来るようにする。
という手順で設計すればOKということになります。
ちなみに、上記の図は Fusion 360 の Spur Gear アドインで作図しています。これで作図してレーザー加工機やCNCルーターで切削する予定です。
