
貨幣と資本(第2回)【補論】旧来の需要・供給モデルに対する数学的批判
マクロ経済理論における旧来のパラダイムの中では、ケインジアンの投資乗数理論において、投資と貯蓄が相互に独立した要因によって決定され、均衡に達すると考える、「需給均衡条件式(方程式)」モデルが主流である。
また、「ミクロ的基礎(Micro-foundation)」に基づく新しい古典派(New classical economics)のRBC(Real Business Cycle: 実物的景気循環)モデルにおいても、コブ・ダグラス型生産関数による供給の制約条件の下、代表的個人(representative agent)の効用最大化という仮定に基づく需要(消費及び余暇消費)との均衡が導かれる。従って、RBCモデルも「需給均衡条件式(方程式)」モデルの範疇に位置付けられる。
投資乗数理論に対する批判
簡単な数値例により、需給均衡条件式(方程式)モデルに基づくIS曲線の不存在、そして「投資」乗数理論の数学的な間違いを示す。
複式簿記においては、原則として一つの取引に対して一つの複式仕訳を行う。そして、複式仕訳においては、恒等式と同様、常に必ず(借方)xxx/(貸方)xxxの両方の金額が一致する構造にある。下記の数値例においても、各段階において左右両辺の金額は全て一致している。
さて、当初(第0段階)、消費(C)70+投資(I)30=国民所得(Y)100の状態から、第1段階で追加的な投資(ΔI)10を行った場合、第2段階以降の国民所得の増加(ΔY)の乗数効果は以下の通りである(数値例①)。なお、以下では限界消費性向(c)0.7と仮定していることから、いわゆる投資乗数は、$${1/(1-c)=1/(1-0.7)=1/0.3=3.33333…}$$となる。
【数値例①】

限界消費性向($${c=1-s}$$)または限界貯蓄性向($${s=1-c}$$)は、ケインジアンの投資乗数[$${1/(1-c)=1/s}$$]を決定する要因でもある。確かに、上記数値例でも、第1段階での追加的な投資(ΔI)10に投資乗数3.33333…を乗じた国民所得の増加(ΔY)が第2段階以降で見られる。
しかし、ここで注目すべきは、この簡単な数値例①でも、各段階において『貯蓄(S)≡投資(I)』という恒等式(identity)が常に成立している点である。
まず、第1段階で追加的な投資(ΔI)10によって生ずる国民所得の増加(ΔY)は同額の10、そしてこの第1段階では消費(C)は一定不変であるから、「貯蓄(S)=国民所得(Y)-消費(C)」と定義される貯蓄の増加(ΔS)も同額の10である。ここから演繹できるのは、第1段階での追加的な投資(ΔI)による国民所得の増加(ΔY)と完全に同額で貯蓄の増加(ΔS)になるという、厳然たる複式簿記における会計恒等式(Accounting Identity)のロジックである。従って、第1段階での追加的な投資(ΔI)による国民所得の増加(ΔY)の場合、その限界的な国民所得の増加(ΔY)に対する限界貯蓄性向(s)は1($${s=1}$$)となり、投資乗数[$${1/s=1}$$]も1、言い換えれば第1段階では(1を超える)乗数効果も発生しないことを意味する。
第1段階での追加的な投資(ΔI)10という取引を記録する複式仕訳は、以下の通りである。
(借方)追加的な投資支出(ΔI)10
(貸方)国民所得の増加(ΔY)10
そして、第1段階では、(貸方)国民所得の増加分(ΔY)10に対応する支出(所得の源泉)は、同額の(借方)追加的な投資支出(ΔI)10のみであるから、これと同額10が貯蓄の増加(ΔS)に振替えられる。具体的には、第1段階での国民所得の増加(ΔY)10の由来は、追加的な投資支出(ΔI)10を行った者から、これを売上10として受取った投資財供給者の所得(ΔY)10であって、その他に第1段階でその所得(ΔY)10から消費支出(ΔC)を行った者はいない ($${ΔC=0}$$)。仮に何らかの消費支出(ΔC)を行った者がいたとすれば、それと同額で消費財供給者の所得(ΔY)が増加するはずであるから、第1段階での国民所得の増加(ΔY)は10を超えることとなる。
従って、第1段階で追加的な投資支出(ΔI)10によって発生した所得(ΔY)10は、一切消費支出($${ΔC=0}$$)に充てられることなく、その全額が貯蓄の増加(ΔS)10となる。定義上、恒等式として「貯蓄(S)≡国民所得(Y)-消費(C)」が常に必ず成立し、かつ、増加した国民所得 (ΔY)10からは一切消費支出($${ΔC=0}$$)がなされない以上、同額で貯蓄の増加(ΔS)10に振替えられるのは、数学的にも当然の理である。
(借方)国民所得の増加(ΔY)10
(貸方)貯蓄の増加(ΔS)10
上記2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳が得られる。
(借方)追加的な投資支出(ΔI)10
(貸方)貯蓄の増加(ΔS)10
この仕訳は、『貯蓄(S)≡投資(I)』が常に成立する恒等式(identity)であることを証明するものである。従って、貯蓄(S)と投資(I)を均衡させる利子率と国民所得(Y)から導かれるIS曲線自体、存在しない。
次に、第2段階以降では、限界的な国民所得の増加(ΔY)に限界消費性向(c)を乗じた消費支出の増加(ΔC)により、文字通り乗数的な国民所得の増大(ΔY)が見られる。しかし、これは本来、「消費」の乗数効果とも呼ぶべきものであって、「投資」乗数理論はその根本から見直されるべきである。
そこで、今度は当初(第0段階)より投資(I)は30で一定不変とする一方、第1段階で追加的な消費(ΔC)10がなされた場合の簡単な数値例を示す(数値例②)。
【数値例②】
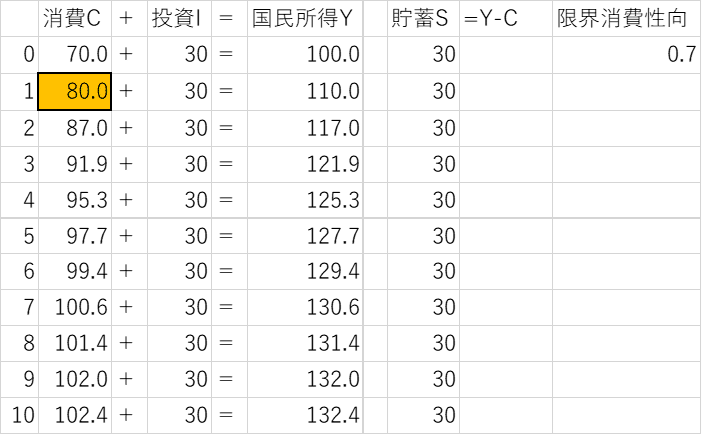
この数値例②では、当初(第0段階)以降、追加的な投資支出は一切行わず(ΔI=0)、他方、第1段階で追加的な消費支出(ΔC)10を行った結果、先の数値例①と全く同様、「投資」乗数($${1/(1-c)=1/(1-0.7)=1/0.3=3.33333…}$$を乗じた国民所得の増大(ΔY)が見られる。従来、「投資」の乗数効果と思われてきたものは、実際には「消費」の乗数効果であったことの証左である。
上記の数値例①及び②において共通するのは、第2段階以降の複式仕訳である。第2段階の仕訳を示すと、以下の通りである。
(借方)追加的な消費支出(ΔC)7
(貸方)国民所得の増加(ΔY)7
これを説明すると、第1段階で発生した国民所得の増加(ΔY)10が家計部門に分配されたと仮定した上で、第2段階でこれに限界消費性向(c)0.7を乗じた消費支出の増加(ΔC)7が発生し、それに伴って第2段階で更なる国民所得の増加(ΔY)7に繋がるということである。従って、第1段階における国民所得の増加(ΔY)の要因(複式仕訳でいえば、借方側)が投資の増加 (ΔI)であろうが、消費の増加(ΔC)であろうが、第2段階以降の乗数的な国民所得の増大(ΔY)には変わりがない。そして、第1段階での限界的な国民所得の増加(ΔY)に限界消費性向(c)を乗じた消費の増加(ΔC)が発生するのは、あくまでも第2段階以降である。
計量経済学による実証研究に期待するところだが、むしろ第2段階以降に限界消費性向(c)を乗じた消費支出の増加(ΔC)と、それによる乗数的な国民所得の増大(ΔY) が実際に発生するのか、言い換えれば本当に投資乗数または投資の乗数効果というものが存在するのか、精緻な検証が不可欠と思われる。
投資と貯蓄が相互に独立した要因によって決定され、均衡に達すると考える需給均衡条件式(方程式)モデルにおいては、追加的な投資(ΔI)10による国民所得の乗数効果(ΔY)は、「$${ΔY=c×10+c^2×10+c^3×10+⋯=10/(1-c)}$$」というプロセスを経て発生すると想定されている。これは、数値例①の第2段階以降の数値と一致する。しかし、数学的に問題となるのは、同プロセスに対応する貯蓄の発生メカニズムである。需給均衡条件式(方程式)モデルにおいては、上記乗数プロセスに対応して「$${ΔS=(1-c)×10+(1-c)c×10+(1-c) c^2×10+⋯=10}$$」という貯蓄の発生メカニズムが想定されている。これは、数値例①の第2段階以降で貯蓄(ΔS)が徐々に増えていき、最終的に極値として第1段階での追加的な投資(ΔI)10に等しくなることを意味する。しかし、そもそも数値例①の第1段階で『貯蓄(S)≡投資(I)』に従い、追加的な投資(ΔI)10と同額で貯蓄の増加(ΔS)10が発生している以上、需給均衡条件式(方程式)モデルで数値例①の第2段階以降に発生するとされる貯蓄(ΔS)10は二重計上となる。
本来、ケインジアンの投資乗数理論は、投資財と消費財から構成される2財モデルである。にもかかわらず、需給均衡条件式(方程式)モデルにおいては、上記の数値例①及び②の第1段階のみが投資財と消費財を区別しない1財モデルとした上で、その第1段階以降に生ずる限界的な国民所得の増加(ΔY)に伴い、第2段階以降で限界消費性向(c)を乗じた消費の増加(ΔC)、限界貯蓄性向(s)を乗じた貯蓄の増加(ΔS)が連続的に発生するという、一方向の因果の流れのみを直感的に考えたのではないか。その結果、恒等式である『貯蓄(S)≡投資(I)』が成立しないという数学的な間違いを犯したものと考えられる。
この投資乗数理論の数学的な間違いは、旧来のパラダイムである需要・供給モデルの中で、価格や利子率、数量等の調整を経てIS曲線上の均衡に達するものとして、投資(I)と貯蓄(S)とは互いに独立した要因によって決定されると考える需給均衡条件式(方程式)モデル自体の欠陥を浮き彫りにしている。
RBCモデルに対する批判
新しい古典派のRBCモデルにおいては、「ミクロ的基礎(Micro-foundation)」と称して、合理的期待を形成する1人の代表的個人(representative agent)の存在を仮定し、彼は「異時点間で動学的に効用最大化」する経済行動を行うと考える。
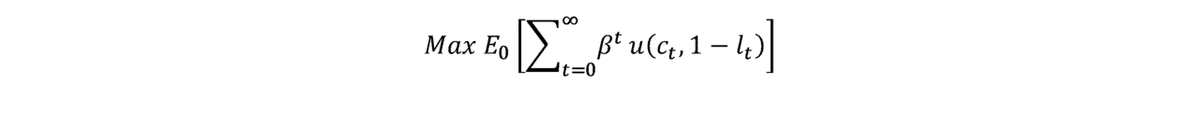
RBCモデルの多くでは、コブ・ダグラス型の生産関数を用いた上で、資本ストックkに関する制約条件を導いている。

その上で、代表的個人(representative agent)の効用最大化の制約条件を以下の通り設定する。

RBCモデルにおいては、上記制約条件に見られるように、資本勘定における『貯蓄(S)≡投資(I)』という恒等式(identity)が組み込まれている点は評価できる。しかし、RBC(実物的景気循環)モデルとの名称の通り、SNAの金融勘定におけるマクロ経済変数の挙動は全く無視されている。
加えて、「ミクロ的基礎(Micro-foundation)」の致命的な問題は、代表的個人(representative agent)の「効用」最大化という、具体的に測定不能な概念を用いて、消費や余暇消費の水準を決定しようとする点にある。どれだけ数学的に精緻な方法を用いたとしても、本来、具体的で測定可能(observable)なマクロ経済変数である消費や余暇消費の水準を正確に予測できないという、理論的に解決できない課題を抱えている。このことは、需給均衡条件式(方程式)モデルにおいて、「効用」最大化という仮定に基づく消費や余暇消費といった「需要」そのものを数学的に正確に予測できないことを意味する。これも需給均衡条件式(方程式)モデルの致命的な欠陥である。
