
第5章 実体的資本蓄積の2つのファイナンス方法
本章においては、貯蓄と投資の関係を複式簿記で分析していく上で、国内のみで経済活動が完結する閉鎖経済を仮定する。
ケインズは「一般理論」の第6章「所得、貯蓄および投資の定義」において、『貯蓄額は個々の消費者の集合行動の結果であり投資額は個々の企業者の集合行動の結果であるにもかかわらず、これら二つの額は、いずれも所得の消費に対する超過額と同等であるから、必ず等しくなる』と述べている。そして、これを簡略化して、以下の恒等式で貯蓄と投資との均衡を示している(Keynes, p.38)。
Income = value of output = consumption + investment.
Saving = income − consumption.
Therefore saving = investment.
ここで各項目を日本語と対応する記号に置き換えると、以下の通りである。
①式 国民所得(Y)=消費(C)+投資(I)
②式 貯蓄(S)=国民所得(Y)-消費(C)
③式 よって、貯蓄(S)=投資(I)
更にケインズは、『貯蓄量と投資量の均等は、一方の生産者、他方の消費者あるいは資本装備の購入者、これら両者の取引が二方向的な性格をもつところから生じる』と述べた上で、『要するに投資活動は本性上、われわれが残余や残差と呼ぶ貯蓄を、投資の分だけ増加させずにはおかないのである』(Keynes,p.39)旨の結論を述べている。
5.1 貯蓄(Equity Finance)による投資
しかし、「一般理論」の続く第7章「貯蓄と投資の意味-続論」において、『大衆が増加した所得を消費と貯蓄に振り分ける割合(限界消費性向と限界貯蓄性向)を「自由選択」した結果、得られる「純正」貯蓄のみが投資家の投資支出の財源となり得る』ことを理由として、貯蓄(≒資本: Equity Finance)による投資のみをケインズは想定していたものと考えられる。ケインズは、以下のようなストーリーにより、借入(Debt finance)による投資を否定している。
『銀行体系の行う信用創造は相応の「純正貯蓄」がなくとも投資を生ぜしめるという発想は、ただひとえに、銀行信用の拡張がもたらす結果の一つだけを切り離して、他の諸結果を無視するところから生じる。』
『大衆は増加した彼らの所得を貯蓄と〔消費〕支出にどのような割合で振り分けるかについて「自由選択」を行う。そのさい、投資を増やすために借入れを行った企業者の意図が、大衆が貯蓄を増やそうとするより速い速度で実現するのは(その投資がどのみち起こったはずの他の企業者の投資の肩代わりである場合を除けば)不可能である。』
『こうしてみると、貯蓄は必ず投資をともなうという旧来の見解は、不完全で誤解を招くおそれがあるとはいえ、論理形式面で見ると、投資がなくとも貯蓄はありうる、あるいは「純正」貯蓄がなくても投資はありうるとする新式の見解よりはよほどまっとうである。』
『大衆の側に賃金単位表示の貯蓄を増やす用意がなければ賃金単位表示の投資の増加は起こりえない。』
このように、ケインズが想定した貯蓄(≒資本: Equity Finance)による投資の場合、投資家は、貯蓄(S)≡資本蓄積(ΔK)という形態で保有するマネーストック(M)を投資支出に活用するという意味で、「貯蓄(S)→投資(I)」という一方向の因果関係を暗黙の仮定(tacit postulate)としているのである。
投資家
貯蓄(≒資本: Equity Finance)による投資の場合、投資家の観点からすれば、具体的なマネーストック(M)の挙動=マネー・フローは以下の通りである。
①式「Y=C+I」によって決定された国民所得(Y)を前提として、②式「S=Y-C」によって貯蓄(S)の金額が決定される。この場合、国民所得(Y)、消費(C)、投資(I)、そして貯蓄(S)はいずれもマネーストック(M)を媒介とする取引から発生するものであるから、4.資本勘定の貸方(右側)で資本(K)ストックに変換される前の貯蓄(S)は、投資家の保有する銀行預金(金融資産)に対応する。同時に、これを銀行の側から見れば、銀行の負債であるマネーストック(M)の形態を取ることとなる。
そして、貯蓄(S)は同額で4.資本勘定の貸方(右側)で資本ストック(ΔKs)に変換(振替)される。他方、その貯蓄(S)に対応するマネーストック(M)は5.金融勘定の貸方(右側)に計上されており、投資と同時に資本財の買手から売手の口座に振替えられる。そして、これと同額で4.資本勘定の借方(左側)で投資(I':純固定資本形成)として記録される。
これらのマネー・フローを投資家の観点による複式仕訳で表現すると、以下の通りである。数値例として、100億円の貯蓄(S)と同額の投資(I':純固定資本形成)支出の場合を示す。[1]
【投資家】
a) 貯蓄の発生及びマネーストックの獲得
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:資本勘定)貯蓄(S)100
b) 投資支出
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
これらa)及びb)の2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、SNAの4.資本勘定における下記の仕訳c)が得られる。
c) 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
(借方:資本勘定)投資(ΔI':純固定資本形成)100
(貸方:資本勘定)貯蓄(ΔS)100
そして、SNAの4.資本勘定の貸方(右側)において、下記の仕訳d)によって貯蓄(S)フローが資本(K)ストックへと変換(振替)される。
d) 貯蓄(S)フローの資本(K)ストックへの変換(振替)
(借方:資本勘定)貯蓄(S)100
(貸方:BS及び資本勘定)資本蓄積(ΔKs)100
出発点の仕訳a)が意味するのは、「最初に貯蓄(S)ありき」ということである。これこそが、ケインズ以降、経済学者が無意識のうちに囚われていた暗黙の仮定(tacit postulate)である。実際、ケインズ自身、「一般理論」の第6章では、恒等式「貯蓄(S)=投資(I)」に関して正しい解釈に到達していながら、第7章に至ると残念なことに直感的な推論に基づく「貯蓄(S)→投資(I)」という一方向の因果関係に囚われていたように見受けられる。
ケインズの業績の偉大さは何人たりとも否定できないが、その偉大さ故に「一般理論」後80年以上にわたって経済学者の思考のパラダイムまで固定化してしまったのではないだろうか。かかるケインズのパラダイムを転換するには、会計恒等式(accounting identity)の観点からSNAをT型勘定に組み替えた上で、ゼロから複式簿記の仕訳のロジックを積み上げていく他はない。
5.2 投資の一般理論
大衆が自由選択により彼らの所得を消費と貯蓄に振り分ける場合、そこで得られる貯蓄をケインズは「純正貯蓄」と呼んだ。そして、ケインズは「純正貯蓄」を超える投資を否定した。しかし、我々の生きる現実の世界では、「純正貯蓄」を超える投資、すなわち借入(Debt finance)による投資が大半である。
そこで、借入(Debt finance)による投資または貯蓄(≒資本: Equity Finance)による投資のいずれかを問わず発生する一般的な複式仕訳、すなわち投資家の仕訳b)に加えて、資本財の売手の仕訳e-1)、e-2)及びe-3)を示す。
投資家
【投資家】
b) 投資支出
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
投資財の売手
投資財(資本財)の売手の観点から、投資財の売上に関するマネー・フローを複式仕訳e)で表現すると、以下の通りである。数値例として、100億円の投資財の売上の場合を示す。なお、投資財の売手の観点からの複式仕訳であるから、投資家が借入(Debt Finance)を財源としているのか、あるいは貯蓄(≒資本: Equity Finance)を財源としているのか、そのいずれであっても一切違いは生じない。
【投資財の売手】
e-1) 総需要(売上)の発生
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:国内総生産勘定)国内総生産(投資財の売上[I':純固定資本形成])100
e-2) 国民所得(Y)への振替
(借方:国内総生産勘定)国内総生産(投資財の売上[I':純固定資本形成])100
(貸方:所得支出勘定)国民所得(Y)100
e-3) 国民所得(Y)の貯蓄(S)への振替
(借方:所得支出勘定)国民所得(Y)100
(貸方:資本勘定)貯蓄(S)100
これら3つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳e)が得られる。
e) 貯蓄の発生及びマネーストックの獲得
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:資本勘定)貯蓄(S)100
手品のように思われるかも知れないが、実は、この投資財の売手の観点による仕訳e)は、貯蓄(≒資本: Equity Finance)による投資の場合の仕訳「a) 貯蓄の発生及びマネーストックの獲得」と全く同一なものである。種も仕掛けもないが、これが複式簿記の厳密なロジック、すなわち会計恒等式(Accounting Identity)から導かれる結論である。
そこで、一国経済全体で投資家の仕訳b)と投資財の売手の仕訳e)の2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、貯蓄(≒資本: Equity Finance)による投資の場合と同様、SNAの4.資本勘定における下記の仕訳c)が得られる。
c) 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
(借方:資本勘定)投資(ΔI':純固定資本形成)100
(貸方:資本勘定)貯蓄(ΔS)100
ここで改めて上記の仕訳b)及びe-1), e-2)に着目した上で、「投資による国民所得の増加(Yi)」に関するこれら3つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳f)が得られる。
f) 投資による国民所得の変動(Yi)
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:所得支出勘定)国民所得(Yi)100
従って、上記の仕訳c)及びf)を合成すると、会計恒等式⑦が得られる。
恒等式⑦ 投資の変動(ΔI)≡ 投資による国民所得の変動(ΔYi)≡貯蓄の変動(ΔS)
そして、恒等式⑦は恒等式⑦-1及び⑦-2に分解できる。
恒等式⑦-1 [借方]投資による国民所得の変動(ΔYi)≡[貸方]貯蓄の変動(ΔS)
恒等式⑦-2 [借方]投資(純固定資本形成)の変動(ΔI')≡[貸方]貯蓄の変動(ΔS)
投資乗数は存在しない
まず、恒等式⑦-1「投資による国民所得の変動(ΔY)≡貯蓄の変動(ΔS)」から解釈できるのは、追加的な「投資(純固定資本形成)の増加(ΔI')」によって発生する限界的な「国民所得の増加(ΔYi)」は、これと同額で「貯蓄の増加(ΔS)」をもたらすという点である。この場合、社会全体としては一切「消費支出(ΔC=0)」はなされていない。
従って、投資による国民所得の増加(ΔYi)の場合、その限界的な国民所得の増加(ΔYi)に対する限界貯蓄性向(s)は常に1で一定(s=1)となる一方、限界消費性向(c)は一切消費がなされていない以上0で一定(c=0)となる。
特に「限界消費性向(c: Marginal Propensity to Consume)」というパラメータは、「1/(1-c)」を乗数とするケインジアンの理論的基礎ともいえる概念である(Keynes, pp.69-71)。しかし、マクロ会計における上記恒等式⑦-1によれば、追加的な投資支出の場合、限界消費性向c=0、従って、ケインジアンの乗数「1/(1-c)」は常に1となり、本来、1を超えるべき乗数としての意味をなさない。
投資貯蓄恒等定理
次に、恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」の意味するところは、借入(Debt Finance)による投資の場合または貯蓄(≒資本)(Equity Finance)による投資の場合のいずれかを問わず、投資(ΔI':純固定資本形成)の変動額と同額で貯蓄(ΔS)が変動するという、厳密な複式簿記における会計恒等式(Accounting Identity)のロジックである。
本稿では、恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」から導かれる命題「投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す(Investment creates its own saving)」を「投資貯蓄恒等定理」と呼ぶこととしたい。
投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す
“Investment creates its own saving”
従来の経済学、すなわち古典派(新古典派)、ケインジアン、あるいは現代マクロ経済学(RBC/DSGEモデル)のいずれにおいても、暗黙の仮定(tacit postulate)として「貯蓄(S)→投資(I)」という一方向の因果関係が理論的前提とされていた。なぜなら、商品貨幣説と同様、投資家の手許に「貯蓄(S)」、すなわち実物資産(金地金/兌換券)としてのマネーがなければ、これを使用して「投資(I)」を行うことはできないと考えられてきたからである。
しかし、信用貨幣説において銀行貸付によって無から有のマネーストックが生み出されるのと同様、仮に投資時に投資家の手許に「貯蓄(S)」がなくとも、投資家は借入(Debt Finance)による投資を行うことは可能である。その場合、投資貯蓄恒等定理に従い、社会全体で見れば「投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す」のである。
従って、閉鎖経済においては、従来の「貯蓄(S)→投資(I)」という一方向の因果関係だけでなく、マクロ会計恒等式として「投資(I)≡貯蓄(S)」という双方向の再帰的(reflexive)関係が常に必ず成立する。
一般的には、ケインズの②式「S=Y-C」に従い、倹約により消費(C)を減らさなければ、貯蓄(S)は増加しないという直感的な推論が働くのは人間の本性ともいえる。例えば、戦時中の標語としても有名な「欲しがりません、勝つまでは」「ぜいたくは敵だ」といった倹約を勧め、貯蓄増加による供給側(supply side)の生産力の増加を図ろうとする政策も実際に行われたのも事実である。また、戦後日本の高度成長の要因分析としても、勤勉な国民性に加え、高い貯蓄率(平均貯蓄性向:APS)が挙げられることが多い。
しかし、基本的な恒等式である国民所得(Y)≡消費(C)+貯蓄(S)に従えば、仮に倹約により消費(ΔC)を削減したとしても、それと同額で国民所得(ΔY)が減少することから、社会全体として見れば貯蓄(S)自体は不変である。なぜなら消費(ΔC)を削減すれば、それと同額(ΔC)で総需要が減少し、消費財の売手(供給側)の国民所得(Y)もΔC分、減少するからである。従って、国民所得(Y)≡消費(C)+貯蓄(S)との恒等式が、国民所得(Y−ΔC)≡消費(C−ΔC)+貯蓄(S)と縮小・変形されるだけであり、貯蓄(S)自体は不変である。
論理的に考えれば自明のことであるのに、人間の思考の枠を狭める旧来のパラダイムの恐ろしい点である。
5.3 借入(Debt Finance)による投資の特殊理論
借入(Debt finance)による投資における取引やマネーストックの流れを複式仕訳で表現すると、以下の通りである。数値例として、100億円の銀行借入と同額の追加的な投資(ΔI)支出の場合を示す。
銀行家
g) 投資家への銀行貸付
(借方:BS及び金融勘定)貸付金100
(貸方:BS及び金融勘定)預金通貨(マネーストック)100
投資家
a') 銀行借入(Debt finance)
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:BS及び金融勘定)借入金100
b) 投資支出
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
貯蓄(≒資本: Equity Finance)による投資との違いは、この仕訳a')の貸方(右側)に計上される勘定科目が4.資本勘定の「貯蓄(S)」から5.金融勘定の「負債」に変わったことである。
投資財の売手
投資財の売手の観点からは、上記投資の一般理論の場合と同様、仕訳e)が発生する。
e) 貯蓄の発生及びマネーストックの獲得
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:資本勘定)貯蓄(S)100
従って、借入(Debt Finance)による投資の場合の銀行家、投資家、そして投資財の売手の上記仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、以下の2つの複式仕訳が得られる。
c) 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:資本勘定)貯蓄(S)100
h)銀行家と投資家との間での債権債務関係
(借方:BS及び金融勘定)貸付金100
(貸方:BS及び金融勘定)借入金100
まず、仕訳c)は、貯蓄(≒資本: Equity Finance)による投資の場合の仕訳c)と全く同一である。それが意味するのは、借入(Debt Finance)による投資の場合であっても、恒等式「貯蓄(S)≡投資(I)」が成立し、従って、投資貯蓄恒等定理「投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す(Investment creates its own saving)」もまた成立するということである。
そして、SNAの4.資本勘定の貸方(右側)において、貯蓄(≒資本: Equity Finance)による投資の場合と同様、仕訳d)によって貯蓄(S)フローが資本(K)ストックへと変換(振替)される。
d) 貯蓄(S)フローの資本(K)ストックへの変換(振替)
(借方:資本勘定)貯蓄(S)100
(貸方:BS及び資本勘定)資本蓄積(ΔKs)100
次に、仕訳h)が意味するのは、銀行家と投資家との間での債権債務関係である。投資家が借入(Debt Finance)による投資を行う場合、マネーストックの変動メカニズムに関する恒等式⑥「銀行システムの金融資産(投融資)の変動≡マネーストックの変動(ΔM)」が成立すると同時に、恒等式「貯蓄(S)=投資(I)」もまた成立する。その意味するところは、借入(Debt Finance)による投資と同額で、①マネーストックの増加(ΔM)及び②貯蓄の増加(ΔS)≡資本蓄積(ΔK)が生ずるということである。
投資貯蓄マネー恒等定理「貨幣は重要である(Money matters.)の経路
借入(Debt Finance)による投資の場合、借入(Debt Finance)による投資と同額で、①マネーストック増加(ΔM)及び②貯蓄の増加(ΔS)≡資本蓄積(ΔK)が生ずる。本稿では、これを「投資貯蓄マネー恒等定理」と呼ぶこととしたい。
借入(Debt Finance)による投資の場合、仮に投資の時点で貯蓄(S)がなくとも、投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)と(固定資本減耗の金額を加算した)マネーストック(ΔM)とを生み出す。
この投資貯蓄マネー恒等定理は、複式簿記における会計恒等式(Accounting Identity)のロジックに基づき、SNAの勘定科目相互間の勘定連絡を表現したものであるから、常に必ず成立する。
これらをまとめると、借入(Debt Finance)による投資の場合、マネーストック増加(ΔM)→投資増加(ΔI')→国民所得増加(ΔY)→貯蓄増加(ΔS)→資本蓄積(ΔK)という流れこそが、「貨幣は重要である(Money matters.)」の経路であることを数学的に証明できる。
借入(Debt Finance)による投資の償還支出
これとは逆に、借入(Debt Finance)による投資の償還支出に関する仕訳i)は、以下の通りである。具体的には、上記仕訳a')の貸方で計上された借入金元本100億円の銀行に対する償還支出100億円を意味する。
【投資家】
i) 償還支出
(借方:BS及び金融勘定)借入金100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
これに対応する銀行の貸付金回収の仕訳は以下の通りである。従って、一国経済全体では、マネーストック100億円が減少する信用収縮が生ずる。
【銀行家】
j)(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:BS及び金融勘定)金融資産(貸付金)100
一国経済全体で見れば上記の通りだが、現実には、100億円の銀行借入の借手であり、かつ、100億円の投資支出を行う事業会社X(投資財の買手)は、その100億円の投資財の売手として100億円の資本蓄積(利益剰余金)を稼得した事業会社Yとは当然のことながら別の会社である。従って、事業会社Xの借入(Debt Finance)による投資の償還支出は、原則として借入金償還支出時までの損益取引によって稼得する資本蓄積(利益剰余金)と減価償却累計額、言い換えればこれに対応する現金預金(マネーストック)を償還(redemption)の原資としなければならない。
第5章付録:商品貨幣説に基づく現代マクロ経済学の誤り②
代表的個人の「ミクロ的集計」と、取引の相手方の複式仕訳も集計する「会計的集計」とは一致しない
本稿では、「ミクロ的基礎」における代表的個人の「ミクロ的集計」と、社会全体から見た場合、すなわち取引主体だけでなく、その取引の相手方の複式仕訳も同時かつ同額で集計する「会計的集計」の違いについて解説する。
以下では、実物面からミクロ的基礎に由来する現代マクロ経済学の誤りを指摘する。
所得と消費
「ミクロ的基礎」によるRBC/DSGEモデルにおいては、代表的個人としての企業が、前期の資本(Kt-1)と当期の労働(Lt)を投入して、当期の生産=所得(Yt)を得ると考える。なお、典型的にはコブ・ダグラス型生産関数が用いられる。
$${Y_t=A_t K_{t-1}^\alpha L_t^{1-\alpha}}$$
Atは全要素生産性、αは資本の生産弾力性。他方、企業は利潤最大化のため、資本コスト(Rt)と労働コスト(Wt)を最小化することを目指す。
重要なのは、当該生産関数(構造方程式)上、生産=所得(Yt)を決定する要素は、あくまでも資本(Kt-1)と労働(Lt)に限定される点である。要は、当期の生産=所得(Yt)の決定には、当期の消費(Ct)も投資(It)も一切無関係であることが仮定されている。
これに対して、マクロ会計学においては、消費財(価格70)・資本財(価格30)の売手と買手の両者において、2つの複式仕訳が発生する。
【売手】 [借方] 現金預金100 / [貸方] 収益(付加価値=粗利Ct70+It30)
【買手】 [借方] 費用(消費支出Ct70)
固定資産(投資支出It30) / [貸方] 現金預金100
従って、社会全体で見れば、GDP(Yt)100の生産=所得が発生する。これを会計恒等式で示すと、
$${[BI]Y_t 100=C_t 70+I_t 30}$$
$${{[BI]S}_t 30=[BI]Y_t100-C_t 70}$$
となる。なお、[BI]とは、会計恒等式を常に必ず成立させる残高調整項目(Balancing Items)を意味する。
RBC/DSGEモデルにおいては、代表的個人としての家計が、消費(Ct)と労働供給(Lt)を選択し、効用関数U(Ct, Lt)を最大化することを目指す。
$${Max U(C_t,L_t)=lnC_t-\varphi L_t}$$
なお、 $${\varphi}$$は労働の不快さを示すパラメータである。
ここで、代表的個人である家計の効用最大化の結果、当期の消費支出(Ct)が変動し、10減少する場合を考えてみよう。このとき、「ミクロ的基礎」によるRBC/DSGEモデルにおいては、当期の生産=所得(Yt)は一定のまま、消費支出(Ct)のみが10減少することとなる。従って、
$${S_t40=Y_t100-C_t60}$$
となり、同額で貯蓄(St)が増加することとなる。しかし、「ミクロ的基礎」によるRBC/DSGEモデルのこのような結果は完全に間違っている。買手側である家計が消費支出(Ct)を10減少させるということは、消費財の売手側の企業から見れば、その生産=所得(Yt)が10減少することを意味するからである。「ミクロ的基礎」によるRBC/DSGEモデルでは、社会全体の所得と家計の消費・貯蓄について、互いに独立した関係の構造方程式が用いられていることが原因である。
これを残高調整項目[BI]を有する社会全体の会計恒等式で見れば、当期の消費支出(Ct)が10減少する場合、これと同額で生産=所得(Yt)が減少し、従って、貯蓄(St)は一定となる。
$${[BI]Y_t 90=C_t 60+I_t 30}$$
$${{[BI]S}_t 30=[BI]Y_t90-C_t 60}$$
「ミクロ的基礎」によるRBC/DSGEモデルにおいては、マクロ変数として最も基礎的な国民所得(Yt)、消費(Ct)、貯蓄(St)について、いかに複雑な計算をしていようとも、現実とは乖離した間違った結果しか得られない。このような理論的にも重大な欠陥は広く認識されるべきである。
貯蓄
現在、主流の実物的景気循環(RBC)モデルや動学的確率一般均衡(DSGE)モデルにおいては、ミクロ的基礎(構造方程式)として、代表的家計の異時点間の効用最大化経路を示す「オイラー方程式」が組み込まれている。なお、オイラー方程式には様々なバリエーションがあり、下記のものはその一例である。
$${u'(c_t)=\beta (1+r) u'(c_{t+1})}$$
u’:効用uの一階微分、ct:第t期)の消費、r:利子率、β:割引率
代表的個人の「ミクロ的集計」では、恒等式「[BI]貯蓄(S)≡[BI]国民所得(Y)-消費(C)」に基づき、「貯蓄は消費によって決定される」と考える。従って、代表的家計の「現在の消費」と「現在の貯蓄」との間のトレードオフ、すなわち効用最大化問題としてオイラー方程式が用いられる際、その最もシンプルな意味としては、「現在の貯蓄」を「(利子分が加算された)将来の消費」に置き換えた上で、「現在の消費」と「(利子分が加算された)将来の消費」との間での異時点間の効用最大化経路を求めるということになる。
確かに一見すると、直感的にオイラー方程式は正しいようにも思える。例えば、一定の所得のある個人が、①現在の消費を諦めて「現在の貯蓄」を増やした場合、将来、②利子分が加算されて「将来の消費」に使うことができるのは当たり前のように見える。
しかし、「現在の消費」と「現在の貯蓄」との間のトレードオフ、具体的には「代表的家計が消費を減らすと貯蓄(将来の消費)が増える(その逆も然り)」という命題は、一定の所得のある個人では成り立つとしても、社会全体としては成り立たたない。
なぜなら、仮に代表的家計が「現在の消費」を諦めた(減少させた)場合、社会全体で見れば、代表的家計の取引の相手方である消費財を売った側の所得が同額で減少するからである。これを社会全体の会計恒等式で表現すれば、「[BI]国民所得(Y-ΔC)≡消費(C-ΔC)+ [BI]貯蓄(S)」となる。「現在の消費」を減少させたとしても、社会全体の「現在の貯蓄」は変化しないのである。
それでは、マクロ変数としての「現在の貯蓄」とは、そもそも何によって決定されるのだろうか。結論を先取りすれば、「現在の貯蓄」は、あくまでも「現在の投資」によってのみ決定される。これを会計恒等式で示すと、「現在の貯蓄(S)」≡「現在の投資(I)」という、おなじみのI-Sバランス式となる。
確かに因果関係に基づく直感的な推論からは「貯蓄という財源があってこそ投資できる」と考えがちだが、同時的(simultaneously)な「貸借一致」を意味する会計恒等式「投資(I)≡[BI]貯蓄(S)」からは、「当初、投資主体に貯蓄がなくとも(借入による投資がなされることで)、社会全体で見れば、投資と同額で資本財を売った側の所得と貯蓄が増加する」といえるのである。
投資
会計恒等式「投資(I)≡[BI]貯蓄(S)」から「貯蓄は投資によって決定される」との命題が導かれる。そして、投資には二つのファイナンス方法がある。一つは自己資本(Equity finance)、すなわち貯蓄による投資であり、もう一つは借入(Debt finance)による投資である。
ミクロ的基礎には、代表的個人の効用最大化の予算制約条件(構造方程式)として、以下の資本遷移式が組み込まれている。
$${K_{t+1}=(1-\delta) K_t +F(K_t,L_t)-C_t}$$
Kt:t期首の資本残高、δ:減価償却率、F(Kt,Lt):生産関数、Ct:消費、Lt:労働
これを見れば明らかだが、資本遷移式の暗黙の前提は、自己資本(貯蓄)によるエクイティ・ファイナンスのみに限定されるということである。特に、RBC(実物的景気循環)モデルではその名の通り実物面にのみ着目し、社会会計の金融勘定やマネーストックといった金融面を完全に無視している。
しかし、エクイティ・ファイナンスであろうが、デット・ファイナンスであろうが(言い換えれば、投資時に投資家に貯蓄[自己資本]があろうがなかろうが)、マクロ経済学が対象とする社会全体として見れば、投資のための資本財を売った側には同額の所得が生じ、従って、社会全体の貯蓄も同額で増加する。ミクロ的基礎の資本遷移式(構造方程式)はこの点を見逃している。
特にデット・ファイナンスの場合には、社会会計上、金融勘定における下記の会計恒等式に従い、投資に充てられる融資と同額で社会全体のマネーストックも増加する。
[借方]銀行システムの金融資産(投融資)の変動≡[貸方]マネーストックの変動
従って、デット・ファイナンスによる投資の場合、マネーストックの増加が、実物面での投資を通じて国民所得、貯蓄、そして資本蓄積に影響を及ぼす。このことは、マクロ経済学上、「貨幣は重要」”Money matters.”であることの証左である。
乗数理論
会計恒等式「投資(I)≡[BI]貯蓄(S)」に加えて、消費を含む会計恒等式「[BI]国民所得(Y)≡消費(C)+投資(I)」について、より詳しく見ていこう。まず、投資と消費それぞれの影響を表す会計恒等式として、以下の二つが成り立つ。
①式 投資の変動(ΔI)≡投資財を売った側の所得の変動(ΔYi)≡社会全体の貯蓄の変動(ΔS)
ΔI≡ΔYi≡ΔS
②式 消費の変動(ΔC)≡消費財を売った側の所得の変動(ΔYc)
ΔC ≡ΔYc
乗数理論の欠陥
上記①式の意味するところは、ある経済主体が「投資支出」を行った場合、投資のための資本財を売った側の経済主体には「投資支出」と同額の所得が生じ、従って、社会全体として見れば、投資と同額の貯蓄も発生するという点にある。結局、会計恒等式「投資(I)≡[BI]貯蓄(S)」が成立する。
他方、上記②式の意味するところは、ある経済主体が「消費支出」を行った場合、消費のための消費財を売った側の経済主体には「消費支出」と同額の所得が生じるが、社会全体として見れば、所得の増加と同額の「消費支出」がなされているので、会計恒等式「[BI]国民所得(Y+ΔC)≡消費(C+ΔC)+[BI]貯蓄(S)」に従い、貯蓄は変化しないという点にある。
一昔前のケインジアンであれば、上記①式の「投資の変動(ΔI)≡投資財を売った側の所得の変動(ΔYi)」という前半部分にのみ着目し、その所得増加に限界消費性向(c: Marginal Propensity to Consume)を乗じて「c・ΔYi」分の追加的な「消費支出」と所得が増加し、その所得増加に更に限界消費性向(c)を乗じた「消費支出」が繰り返しなされることによって乗数効果(multiplier effect)が生ずると主張するだろう。
しかし、①式「投資支出」(ΔI)による最初の所得増加(ΔYi)はあくまでも「投資財を売った側の所得の変動(ΔYi)」であって、これを社会全体の立場から見れば、この所得増加(ΔYi)は全額「投資支出」(ΔI)から生じたものといえる。この場合、社会全体としては一切「消費支出」はなされていない。従って、上記①式「投資の変動(ΔI)≡投資財を売った側の所得の変動(ΔYi)≡社会全体の貯蓄の変動(ΔS)」が成立し、結果として「投資の変動(ΔI)≡社会全体の貯蓄の変動(ΔS)」も成立するのである。
ケインズの「一般理論」(1936)で紹介された「限界消費性向(c: Marginal Propensity to Consume)」というパラメータは、「1/(1-c)」を乗数とするケインジアンの理論的基礎ともいえる概念である。しかし、社会会計における上記会計恒等式によれば、①式:追加的な投資支出の場合、限界消費性向c=0、②式:追加的な消費支出の場合、限界消費性向c=1となる。従って、ケインジアンの乗数「1/(1-c)」は、①式の場合:1、②式の場合: ∞となり、いずれも意味をなさない。
投資乗数と貯蓄の発生メカニズム(具体的数値例)
[追加的な投資の場合]当初(第0段階)、消費(C)70+投資(I)30=国民所得(Y)100の状態から、第1段階で追加的な投資(ΔI)10を行った場合、第2段階以降の国民所得の増加(ΔY)の乗数効果は以下の通りである(数値例①)。なお、以下では限界消費性向(c)0.7と仮定していることから、いわゆる投資乗数は、1/(1-c)=1/(1-0.7)=1/0.3=3.33333…となる。
【数値例①】
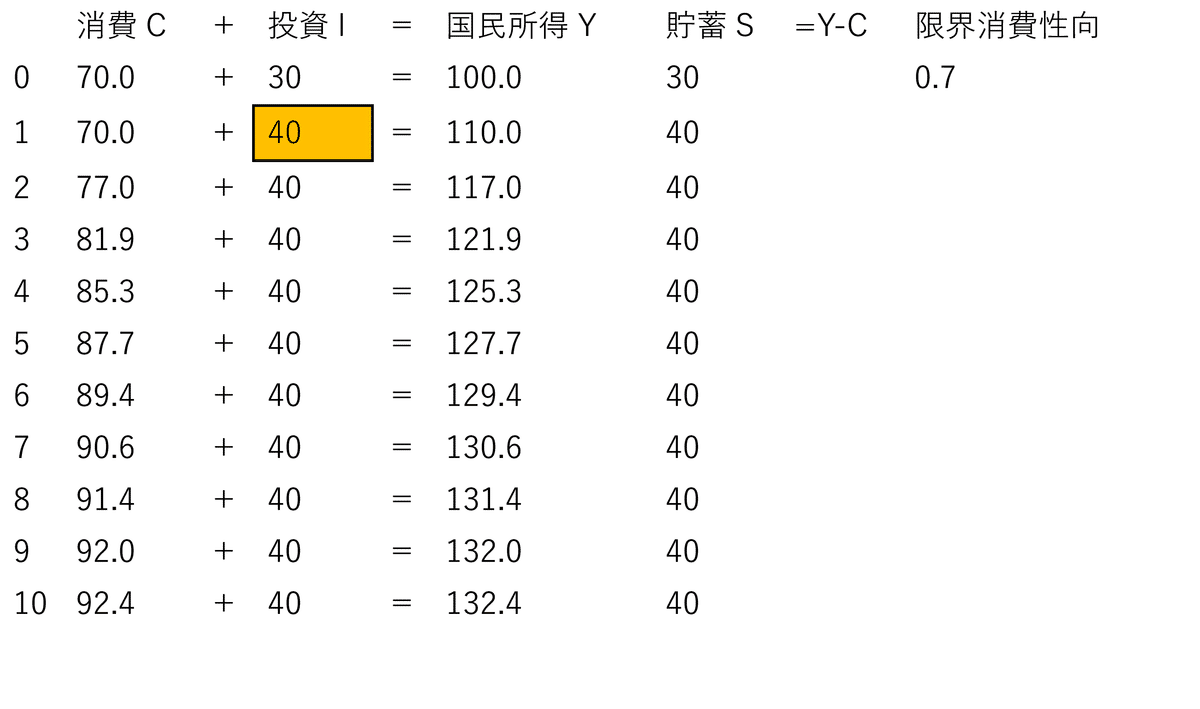
限界消費性向(c=1-s)または限界貯蓄性向(s=1-c)は、ケインジアンの投資乗数[1/(1-c)=1/s]を決定する要因でもある。確かに、上記数値例①でも、第1段階での追加的な投資(ΔI)10に投資乗数3.33333…を乗じた国民所得の増加(ΔY)が第2段階以降で見られる。
しかし、ここで注目すべきは、この数値例①でも、各段階において『貯蓄(S)≡投資(I)』という恒等式(identity)が常に成立している点である。
まず、第1段階での追加的な投資(ΔI)10という取引を記録する複式仕訳は、以下の通りである。
(借方)追加的な投資 (ΔI)10
(貸方)国民所得の増加(ΔY)10
そして、第1段階では、(貸方)国民所得の増加分(ΔY)10に対応する支出(所得の源泉)は、同額の(借方)追加的な投資 (ΔI)10のみであるから、これと同額10が貯蓄の増加(ΔS)に振替えられる。具体的には、第1段階での国民所得の増加(ΔY)10の由来は、追加的な投資 (ΔI)10を行った者から、これを売上10として受取った投資財供給者の所得(ΔY)10であって、その他に第1段階でその所得(ΔY)10から消費支出(ΔC)を行った者はいない (ΔC=0)。仮に何らかの消費支出(ΔC)を行った者がいたとすれば、それと同額で消費財供給者の所得(ΔY)が増加するはずであるから、第1段階での国民所得の増加(ΔY)は10を超えることとなる。
従って、第1段階で追加的な投資 (ΔI)10によって発生した所得(ΔY)10は、一切消費支出(ΔC=0)に充てられることなく、その全額が貯蓄の増加(ΔS)10となる。定義上、恒等式として「貯蓄(S)≡国民所得(Y)-消費(C)」が常に必ず成立し、かつ、増加した国民所得 (ΔY)10からは一切消費支出(ΔC=0)がなされない以上、同額で貯蓄の増加(ΔS)10に振替えられるのは、数学的にも当然の理である。
(借方)国民所得の増加(ΔY)10
(貸方)貯蓄の増加(ΔS)10
上記2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳が得られる。
(借方)追加的な投資 (ΔI)10
(貸方)貯蓄の増加(ΔS)10
以上、厳密な複式簿記のロジックにより、追加的な投資の第1段階として、①式「ΔI≡ΔYi≡ΔS」が常に必ず成立することを証明した。
次に、第2段階以降では、限界的な国民所得の増加(ΔY)に限界消費性向(c)を乗じた消費支出の増加(ΔC)により、文字通り乗数的な国民所得の増大(ΔY)が見られる。言い換えれば、第2段階以降、②式「ΔC ≡ΔYc」が循環的に成立することを意味する。しかし、これは本来、「消費」の乗数効果とも呼ぶべきものであって、「投資」乗数理論はその根本から見直されるべきである。
[追加的な消費の場合]今度は当初(第0段階)より投資(I)は30で一定不変とする一方、第1段階で追加的な消費(ΔC)10がなされた場合の簡単な数値例②とそれに対応する仕訳例を示す。
【数値例②】

この数値例②では、当初(第0段階)以降、追加的な投資支出は一切行わず(ΔI=0)、他方、第1段階で追加的な消費支出(ΔC)10を行った結果、先の数値例①と全く同様、「投資」乗数(1/(1-c)=1/(1-0.7)=1/0.3)3.33333…を乗じた国民所得の増大(ΔY)が見られる。従来、「投資」の乗数効果と思われてきたものは、実際には「消費」の乗数効果であったことの証左である。
上記の数値例①及び②において共通するのは、第2段階以降の複式仕訳である。第2段階以降の②式「ΔC ≡ΔYc 」に関する仕訳を示すと、以下の通りである。
(借方)追加的な消費支出(ΔC)7
(貸方)国民所得の増加(ΔY)7
これを説明すると、第1段階で発生した国民所得の増加(ΔY)10が家計部門に分配されたと仮定した上で、第2段階でこれに限界消費性向(c)0.7を乗じた消費支出の増加(ΔC)7が発生し、それに伴って第2段階で更なる国民所得の増加(ΔY)7に繋がるということである。
従って、第1段階における国民所得の増加(ΔY)の要因(複式仕訳でいえば、借方側)が投資の増加 (ΔI)であろうが、消費の増加(ΔC)であろうが、第2段階以降の乗数的な国民所得の増大(ΔY)には変わりがない。そして、第1段階での限界的な国民所得の増加(ΔY)に限界消費性向(c)を乗じた消費の増加(ΔC)が発生するのは、あくまでも第2段階以降である。
投資と貯蓄が相互に独立した要因によって決定され、均衡に達すると考えるケインジアンの「需給均衡条件式(方程式)モデル」においては、追加的な投資(ΔI)10による国民所得の乗数効果(ΔY)は、限界消費性向c=0.7の場合、
$${ΔY=c×10+c^2×10+c^3×10+⋯= 10⁄(1-c)=33.3333…}$$
というプロセスを経て発生すると想定されている。確かにこれは数値例①及び②の第2段階以降の数値と一致する。
しかし、数学的に問題となるのは、同プロセスに対応する貯蓄の発生メカニズムである。需給均衡条件式(方程式)モデルにおいては、上記乗数プロセスに対応して
$${ΔS=(1-c)×10+(1-c)c×10+(1-c) c^2×10+⋯=10}$$
という貯蓄の発生メカニズムが想定されている。これは、数値例①の第2段階以降で貯蓄(ΔS)が徐々に増えていき、最終的に極値として第1段階での追加的な投資(ΔI)10に等しくなることを意味する。
しかし、数値例①の場合、その第1段階で『貯蓄(S)≡国民所得(Y)-消費(C)』及び『貯蓄(S)≡投資(I)』に従い、追加的な投資(ΔI)10と同額で貯蓄の増加(ΔS)10が発生している以上、需給均衡条件式(方程式)モデルで数値例①の第2段階以降に発生するとされる貯蓄(ΔS)10は二重計上となる。他方、数値例②の場合、追加的な投資(ΔI=0)は一切なされていないにもかかわらず、貯蓄(S)のみが10増加することになる。いずれも数学的な間違いは明らかである。
[1] なお、100億円の貯蓄(S)はキャッシュの変動を伴わない固定資本減耗を控除した後の純貯蓄であるから、現実の「現金預金(マネーストック)=総貯蓄=総投資(I:総固定資本形成)」の金額は「100億円+固定資本減耗」となることに留意を要する。
