
貨幣と資本(第8回):第6章 リアルな実体的資本蓄積(ΔKs)の2つのファイナンス方法
ケインズは「一般理論」の第6章「所得、貯蓄および投資の定義」において、『貯蓄額は個々の消費者の集合行動の結果であり投資額は個々の企業者の集合行動の結果であるにもかかわらず、これら二つの額は、いずれも所得の消費に対する超過額と同等であるから、必ず等しくなる』と述べている。そして、これを簡略化して、以下の恒等式で貯蓄と投資との均衡を示している(Keynes, p.38)。
Income = value of output = consumption + investment.
Saving = income − consumption.
Therefore saving = investment.
ここで各項目を日本語と対応する記号に置き換えると、以下の通りである。
①式 国民所得(Y)=消費(C)+投資(I)
②式 貯蓄(S)=国民所得(Y)-消費(C)
③式 よって、貯蓄(S)=投資(I)
更にケインズは、『貯蓄量と投資量の均等は、一方の生産者、他方の消費者あるいは資本装備の購入者、これら両者の取引が二方向的な性格をもつところから生じる』と述べた上で、『要するに投資活動は本性上、われわれが残余や残差と呼ぶ貯蓄を、投資の分だけ増加させずにはおかないのである』(Keynes,p.39)旨の結論を述べている。
6-1. 貯蓄(≒資本: Equity Finance)による投資
しかし、「一般理論」の続く第7章「貯蓄と投資の意味-続論」において、『大衆が増加した所得を消費と貯蓄に振り分ける割合(限界消費性向と限界貯蓄性向)を「自由選択」した結果、得られる「純正」貯蓄のみが投資家の投資支出の財源となり得る』ことから、貯蓄(≒資本: Equity Finance)による投資のみをケインズは想定していた。ケインズは、以下のような筋書きで借入(Debt finance)による投資を否定している。
『銀行体系の行う信用創造は相応の「純正貯蓄」がなくとも投資を生ぜしめるという発想は、ただひとえに、銀行信用の拡張がもたらす結果の一つだけを切り離して、他の諸結果を無視するところから生じる。』(Keynes, p.38)
『大衆は増加した彼らの所得を貯蓄と〔消費〕支出にどのような割合で振り分けるかについて「自由選択」を行う。そのさい、投資を増やすために借入れを行った企業者の意図が、大衆が貯蓄を増やそうとするより速い速度で実現するのは(その投資がどのみち起こったはずの他の企業者の投資の肩代わりである場合を除けば)不可能である。』(Keynes, p.38)
『こうしてみると、貯蓄は必ず投資をともなうという旧来の見解は、不完全で誤解を招くおそれがあるとはいえ、論理形式面で見ると、投資がなくとも貯蓄はありうる、あるいは「純正」貯蓄がなくても投資はありうるとする新式の見解よりはよほどまっとうである。』(Keynes, p.38)
『大衆の側に賃金単位表示の貯蓄を増やす用意がなければ賃金単位表示の投資の増加は起こりえない。』(Keynes,p.72)
このように、ケインズが想定した貯蓄(≒資本: Equity Finance)による投資の場合、投資家は、貯蓄(S)≡資本蓄積(ΔK)という形態のマネーストック(M)を投資支出に活用すると考えるのである。
投資家
投資家の観点からすれば、具体的なマネーストック(M)の挙動は以下の通りとなる。①式「Y=C+I」によって決定された国民所得(Y)を前提として、②式「S=Y-C」によって貯蓄(S)の金額が決定される。この場合、国民所得(Y)、消費(C)、投資(I)、そして貯蓄(S)はいずれもマネーストック(M)を媒介とする取引から発生するものであるから、3-2.資本勘定の貸方(右側)で資本(K)ストックに変換される前の貯蓄(S)は、必ず一旦は銀行の負債であるマネーストック(M)の形態を取る。
貯蓄(S)は、同額で3-2.資本勘定の貸方(右側)で資本(K)ストックに変換(振替)される。他方、その貯蓄(S)の形態にあったマネーストック(M)は3-3.金融勘定の貸方(右側)に計上されると同時に、それと同額で3-2.資本勘定の借方(左側)で投資(I':純固定資本形成)支出として記録される。
この流れを投資家の観点による複式仕訳で表現すると、以下の通りである。数値例として、100億円の貯蓄(S)と同額の投資(I':純固定資本形成)支出の場合を示す。なお、100億円の貯蓄(S)はキャッシュの変動を伴わない固定資本減耗控除後の純貯蓄であるから、現実の「現金預金(マネーストック)=総貯蓄=総投資(I:総固定資本形成)」の金額は「100億円+固定資本減耗」となることに留意を要する。
a) 貯蓄の発生及びマネーストックの獲得
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:資本勘定)貯蓄(S)100
b) 投資支出
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
この2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、SNAの3-2.資本勘定の貸方(右側)における下記の仕訳c)が得られる。
c) 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:資本勘定)貯蓄(S)100
そして、SNAの3-2.資本勘定の貸方(右側)において、下記の仕訳d)によって貯蓄(S)フローが資本(K)ストックへと変換(振替)される。
d) 貯蓄(S)フローの資本(K)ストックへの変換(振替)
(借方:資本勘定)貯蓄(S)100
(貸方:BS及び資本勘定)資本蓄積(ΔK)100
出発点の仕訳a)が意味するのは、「最初に貯蓄(S)ありき」ということである。これこそが、ケインズ以降、経済学者が無意識のうちに囚われていた暗黙の仮定(tacit postulate)である。実際、ケインズ自身、「一般理論」の第6章では、恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」に関して正しい解釈に到達していながら、第7章に至ると残念なことに直感的な推論に基づく「貯蓄(S)→投資(I)」という一方向の因果関係に囚われていたように見受けられる。
ケインズの業績の偉大さは何人たりとも否定できないが、その偉大さ故に「一般理論」後80年以上にわたって経済学者の思考のパラダイムまで固定化してしまったのではないだろうか。かかるケインズのパラダイムを転換するには、会計恒等式(accounting identity)の観点からSNAをT型勘定に組み替えた上で、ゼロから複式簿記の仕訳のロジックを積み上げていく他はない。
6-2. 借入(Debt Finance)による投資の特殊理論
借入(Debt finance)による投資における取引や資金の流れを複式仕訳で表現すると、以下の通りである。数値例として、100億円の銀行借入と同額の追加的な投資(ΔI)支出の場合を示す。
銀行家
e) 投資家への銀行貸付
(借方:BS及び金融勘定)貸付金100
(貸方:BS及び金融勘定)預金通貨(マネーストック)100
投資家
a') 銀行借入(Debt finance)
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:BS及び金融勘定)借入金100
b) 投資支出
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
貯蓄(≒資本: Equity Finance)による投資との違いは、この仕訳a')の貸方(右側)に計上される勘定科目が3-2.資本勘定の「貯蓄(S)」から3-3.金融勘定の「負債」に変わったことである。
投資財の売手
実際、「貯蓄(S)→投資(I)」という一方向の因果の流れだけでなく、銀行からの借入(Debt finance)による投資の場合には、逆方向の因果の流れ、すなわち「投資(I)→貯蓄(S)」も成立し得る。ここで、投資財の売手の観点から、その流れを複式仕訳f)で表現すると、以下の通りである。数値例として、100億円の投資財の売上の場合を示す。
f-1) 総需要(売上)の発生
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:国内総生産勘定)国内総生産(投資財の売上[I':純固定資本形成])100
f-2) 国民所得(Y)への振替
(借方:国内総生産勘定)国内総生産(投資財の売上[I':純固定資本形成])100
(貸方:所得支出勘定)国民所得(Y)100
f-3) 貯蓄(S)への振替
(借方:所得支出勘定)国民所得(Y)100
(貸方:資本勘定)貯蓄(S)100
この3つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳f)が得られる。
f) 貯蓄の発生及びマネーストックの獲得
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:資本勘定)貯蓄(S)100
手品のように思われるかも知れないが、実は、この投資財の売手の観点による仕訳d)は、貯蓄(≒資本: Equity Finance)による投資の場合の仕訳a)と全く同一なものである。種も仕掛けもないが、これが複式簿記の厳密なロジック、すなわち会計恒等式(Accounting Identity)から導かれる結論である。
従って、借入(Debt Finance)による投資の場合の銀行家、投資家、そして投資財の売手の上記仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、以下の2つの複式仕訳が得られる。
g)銀行家と投資家との間での債権債務関係
(借方:BS及び金融勘定)貸付金100
(貸方:BS及び金融勘定)借入金100
c) 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
(借方:資本勘定)投資(I':純固定資本形成)100
(貸方:資本勘定)貯蓄(S)100
仕訳g)が意味するのは、銀行家と投資家との間での債権債務関係である。投資家が契約通りに元本及び金利を償還している間は良いが、仮に投資家が当該投資によって取得した資産によって生み出される将来キャッシュ・インフローが目論見通りに行かず、銀行の貸付金が不良債権化した場合、全てが逆回転する。銀行家は、不良債権処理として貸倒引当金繰入額または貸倒損失を計上し、その分、銀行の金融資産(投融資)残高を減少させなければならない。そして、銀行システムの恒等式⑥「銀行の金融資産(投融資)の変動≡マネーストック増殖額(ΔM)」が成立しなくなり、マネーストック(M)の安定性への信頼が揺らげば、取り付け騒ぎ等のパニックや銀行システム全体の金融危機が発生することを忘れてはならない。
仕訳c)が意味するのは、恒等式「貯蓄(S)=投資(I)」である。そして、SNAの3-2.資本勘定の貸方(右側)において、下記の仕訳d)によって貯蓄(S)フローが資本(K)ストックへと変換(振替)される。
d) 貯蓄(S)フローの資本(K)ストックへの変換(振替)
(借方:資本勘定)貯蓄(S)100
(貸方:BS及び資本勘定)資本蓄積(ΔK)100
「貨幣は重要である(Money matters.)の経路
従って、上記仕訳c)と等値である恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」こそ、命題①「事後的(ex-post)に常に必ず投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す(Investment creates its own saving)」ことを証明するものである。
命題①「事後的(ex-post)に常に必ず投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す(Investment creates its own saving)。」
そして、借入(Debt Finance)による投資の場合、恒等式⑥'「銀行借入(Debt Finance)の増加額≡銀行の金融資産(投融資)の変動≡マネーストック増殖額(ΔM)」も同時に成立するので、これを合成した命題②が得られる。
命題②「借入(Debt Finance)による投資の場合、仮に投資の時点で貯蓄(S)がなくとも、事後的(ex-post)に常に必ず投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)と(固定資本減耗の金額を加算した)マネーストック(ΔM)とを生み出す」。
この命題②は、複式簿記における会計恒等式(Accounting Identity)のロジックに基づき、SNAの勘定科目相互間の勘定連絡を表現したものであるから、常に必ず成立する。
これらをまとめると、借入(Debt Finance)による投資の場合、マネーストック増加(ΔM)→投資増加(ΔI')→国民所得増加(ΔY)→貯蓄増加(ΔS)→資本蓄積(ΔK)という流れこそが、「貨幣は重要である(Money matters.)の経路ということができる。
借入(Debt Finance)による投資の償還支出
借入(Debt Finance)による投資の償還支出に関する仕訳h)は、以下の通りである。具体的には、上記仕訳a')の貸方で計上された負債元本100億円の銀行に対する償還支出100億円を意味する。
【投資家】
h) 償還支出
(借方:BS及び金融勘定)負債100
(貸方:BS及び金融勘定)現金預金(マネーストック)100
これに対応する銀行の貸付金回収の仕訳は以下の通りである。従って、一国経済全体では、マネーストック100億円が減少する信用収縮が生ずる。
【銀行】
(借方:BS及び金融勘定)現金預金(マネーストック)100
(貸方:BS及び金融勘定)金融資産(貸付金)100
一国経済全体で見れば上記の通りだが、現実には、100億円の銀行借入の借手であり、かつ、100億円の投資支出を行う事業会社X(投資財の買手)は、その100億円の投資財の売手として100億円の資本蓄積(利益剰余金)を稼得した事業会社Yとは別会社である。従って、事業会社Xの借入(Debt Finance)による投資の償還支出は、原則として借入金償還支出時までの損益取引によって稼得する資本蓄積(利益剰余金)と減価償却累計額、言い換えればこれに対応する現金預金(マネーストック)を償還(redemption)の原資としなければならない。
6-3. 借入(Debt finance)・貯蓄(≒資本: Equity Finance)による投資の一般理論
借入(Debt finance)による投資または貯蓄(≒資本: Equity Finance)による投資のいずれかを問わず、投資に関する以下の2つの恒等式は、複式簿記の貸借一致のロジックに基づき、常に必ず成立する。
恒等式⑦-1 投資による国民所得の変動(ΔY)≡貯蓄の変動(ΔS)
恒等式⑦-2 投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)
恒等式⑦-1及び⑦-2の持つ意味については、経済成長理論としても多くの重要な解釈が可能であるが、直感的にはやや理解しづらいかも知れない。そこでまず、以下のSNA上の投資乗数理論の仕訳例によってこれを証明する。
[事例]当初(第0段階)、消費(C)70+投資(I)30=国民所得(Y)100の状態から、第1段階で追加的な投資(ΔI)10を行った場合、第1段階での追加的な投資(ΔI)10という取引を記録する複式仕訳は、以下の通りである。
(借方)追加的な投資支出(ΔI)10
(貸方)国民所得の増加(ΔY)10
そして、第1段階では、(貸方)国民所得の増加分(ΔY)10に対応する支出(所得の源泉)は、同額の(借方)追加的な投資支出(ΔI)10のみであるから、これと同額10が貯蓄の増加(ΔS)に振替えられる。具体的には、第1段階での国民所得の増加(ΔY)10の由来は、追加的な投資支出(ΔI)10を行った者から、これを売上10として受取った投資財供給者の所得(ΔY)10であって、その他に第1段階でその所得(ΔY)10から消費支出(ΔC)を行った者はいない (ΔC=0)。仮に何らかの消費支出(ΔC)を行った者がいたとすれば、それと同額で消費財供給者の所得(ΔY)が増加するはずであるから、第1段階での国民所得の増加(ΔY)は10を超えることとなる。従って、第1段階で追加的な投資支出(ΔI)10によって発生した所得(ΔY)10は、一切消費支出(ΔC=0)に充てられることなく、その全額が貯蓄の増加(ΔS)10となる。定義上、恒等式として「貯蓄(S)≡国民所得(Y)-消費(C)」が常に必ず成立し、かつ、増加した国民所得 (ΔY)10からは一切消費支出(ΔC=0)がなされない以上、同額で貯蓄の増加(ΔS)10に振替えられるのは、数学的にも当然の理である。
(借方)国民所得の増加(ΔY)10
(貸方)貯蓄の増加(ΔS)10
上記2つの仕訳をまとめると(貸借同額の勘定科目を相殺消去すると)、下記の仕訳が得られる。
(借方)追加的な投資支出(ΔI)10
(貸方)貯蓄の増加(ΔS)10
以上、厳密な複式簿記のロジックにより、恒等式⑦-1「投資による国民所得の変動(ΔY)≡貯蓄の変動(ΔS)」及び恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」が常に必ず成立することを証明した。
また、ケインズの「一般理論」の上記①②③式から、同様の結論を導くことも可能である。借入(Debt finance)による投資の場合、投資主体に投資(I)支出時にそれに見合う貯蓄(S)がなくとも、借入(Debt finance)によって調達したマネーストック(ΔM)を財源として追加的な投資(ΔI)支出を行うことができる。従って、「一般理論」の上記①②③式は、次のように変換できる。
①’式 Y+ΔY(=ΔI) =C+(I+ΔI)
②’式 S+ΔS(=ΔI)= Y+ΔY(=ΔI)-C
③’式 ∴ ΔY=ΔS=ΔI
なお、上記③’式は、恒等式⑦-1及び⑦-2と全く等値である。
そして、上記③式「S=I」及び③'式「ΔY=ΔS=ΔI」から等式「S+ΔS=I+ΔI」が得られる。等式「S+ΔS=I+ΔI」から直接的に解釈できるのは、貯蓄(SまたはS+ΔS)の金額の決定要因(determinant)は、投資(I)及び追加的な投資(ΔI)だということである。逆に言えば、会計恒等式(accounting identity)の観点からは、消費(C)の金額がどうあれ、貯蓄(SまたはS+ΔS)の金額の決定とは無関係である。
投資による国民所得増加(ΔY)の限界貯蓄性向一定(s=1)の法則
恒等式⑦-1「投資による国民所得の変動(ΔY)≡貯蓄の変動(ΔS)」から解釈できるのは、追加的な「投資(純固定資本形成)の増加(ΔI')」によって発生する限界的な「国民所得の増加(ΔY)」は、これと同額で「貯蓄の増加(ΔS)」をもたらすという点である。
従って、投資による国民所得の増加(ΔY)の場合、その限界的な国民所得の増加(ΔY)に対する限界貯蓄性向(s)は1で一定(s=1)となることから、本稿では、本稿では、この命題を「投資による国民所得増加(ΔY)の限界貯蓄性向一定($${s=1}$$)の法則」と名付ける。

限界消費性向($${c=1-s}$$)または限界貯蓄性向($${s=1-c}$$)は、ケインジアンの投資乗数[$${1/(1-c)=1/s}$$]を決定する要因でもある。数学的にはこれと同値だが、ケインズの「一般理論」では投資乗数を[k]、限界消費性向を[$${1-1/k}$$]とする以下の記述がある。
『$${∆C_w}$$と$${∆I_w}$$をそれぞれ消費と投資の増加分とすると、$${∆Y_w=∆C_w+∆I_w}$$となり、それゆえ、この関係は$${∆Y_w=k∆I_w}$$という形に書くことができる。[限界消費性向をkを用いて表すと]$${1-1/k}$$が限界消費性向となる。kを投資乗数と呼ぶことにしよう。それは、総投資の増加があると、所得は投資の増加分をk倍した額だけ増加することを教えてくれる』(Keynes, 1936, p.71)。
会計恒等式の観点からすれば、偉大なケインズでさえ、ここで直感的な推論に基づく痛恨のミスを犯している。その数学的な理由は以下の通りである。
① ケインズが示す恒等式$${∆Y_w=∆C_w+∆I_w}$$は常に必ず成立する。その場合、左辺の国民所得の増加$${∆Y_w}$$の内訳として、投資財の売上$${∆Y_{wI}}$$=支出$${∆I_w}$$及び消費財の売上$${∆Y_{wC}}$$=支出$${∆C_w}$$も成立するので、結果として、$${∆Y_w=∆Y_{wI}+∆Y_{wC}=∆C_w+∆I_w}$$もまた常に必ず成立する。
② ケインズの投資乗数k(>1と仮定)を含む$${∆Yw=k∆Iw}$$と上記恒等式$${∆Yw=∆Cw+∆Iw}$$の左辺はいずれも$${∆Yw}$$で等しい。従って、これを等号で結ぶと、以下の数式が得られる。
$${k∆I_w=∆C_w+∆I_w}$$
$${(k-1)∆I_w=∆C_w}$$
ここで、投資乗数kについて、ケインズは『総投資の増加があると、所得は投資の増加分をk倍した額だけ増加する』と述べている。そこで、純粋に投資のみが[$${∆I_w}$$]増加し、消費は不変[$${∆Cw=0}$$]という場合の国民所得に対する乗数効果kについて思考実験を行ってみよう。
この場合、$${(k-1)∆I_w=0}$$であり、投資の増加分[$${∆I_w}$$]が一定のプラスの金額のとき、投資乗数$${k(>1)}$$の仮定に反し、投資乗数は$${k=1}$$でなければならない。逆に言えば、上記の数式$${(k-1)∆I_w=∆C_w}$$が意味するのは、投資(ΔI)による国民所得(ΔY)の乗数効果のうち、1を超える部分$${(k-1)∆I_w}$$は、投資(ΔI)の増加によって発生した訳ではなく、投資金額とは全く無関係に、あくまでも消費(ΔC)の増加と同額で増加した国民所得($${∆Y_{wC}=ΔC_w}$$)に過ぎない。要するに、ケインズの投資乗数kの1を超える部分は、直感的な推論では、一見、投資の増加分[$${∆I_w}$$]に対する乗数効果としての国民所得の増加分[$${∆Y_{wI}}$$]のように見えるが、実は、これは単に消費の増加分[$${∆C_w}$$]に対応した国民所得の増加分[$${∆Y_{wC}}$$]に過ぎないのである。
投資(純固定資本形成)の変動(ΔI’)≡貯蓄の変動(ΔS)
恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」の意味するところは、借入(Debt Finance)による投資の場合または貯蓄(≒資本)(Equity Finance)による投資の場合のいずれかを問わず、投資(ΔI':純固定資本形成)の変動額と同額で貯蓄(ΔS)が変動するという、厳密な複式簿記における会計恒等式(Accounting Identity)のロジックである。

既に指摘したように、従来、マクロ経済学の経済成長理論や動学的確率的一般均衡(DSGE)においては、SNA上、2.国内総生産勘定で発生した国民所得(Y)のうち、消費($${C=C_1+cY}$$)に支出された後の残余(residual)である貯蓄(S≒資本蓄積ΔK)を財源とする投資(I’:純固定資本形成)がなされるという一方向の因果の流れ、すなわち「貯蓄(S≒資本蓄積ΔK)→投資(I’:純固定資本形成)」という無意識かつ暗黙の仮定(tacit postulate)が置かれていた。これを言い換えれば、貯蓄(≒資本)(Equity Finance)による投資のみを想定していたに過ぎない。
しかし、現実には、恒等式⑦-2「投資(純固定資本形成)の変動(ΔI')≡貯蓄の変動(ΔS)」が示すように、「貯蓄(S≒資本蓄積ΔK)→投資(I’:純固定資本形成)」という一方向の因果の流れだけでなく、逆方向の因果関係、すなわち「投資(I':純固定資本形成)→貯蓄(ΔS≒資本蓄積ΔK)」という因果の流れも常に必ず成立する。従って、命題①「事後的(ex-post)に常に必ず投資(I’)自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す(Investment creates its own saving)」も常に必ず成立するのである。
更に付け加えると、追加的な投資(ΔI)が増加すればするほど、平均貯蓄性向(APS: average propensity to save)もまた、下記の数式に従い、上昇していく。
平均貯蓄性向(APS)$${=\dfrac {S+∆S(=∆I)} {Y+∆Y(=∆I)}}$$
一般的には、ケインズの②式「S=Y-C」に従い、倹約により消費(C)を減らさなければ、貯蓄(S)は増加しないという直感的な推論が働くのは人間の本性ともいえる。例えば、戦時中の標語としても有名な「欲しがりません、勝つまでは」「ぜいたくは敵だ」といった倹約を勧め、貯蓄増加による供給側(supply side)の生産力の増加を図ろうとする政策も実際に行われたのも事実である。また、戦後日本の高度成長の要因分析としても、勤勉な国民性に加え、高い貯蓄率(平均貯蓄性向:APS)が挙げられることが多い。
しかし、現実には、恒等式「貯蓄(S)≡投資(I)」から、追加的な投資支出ΔIを行った場合、同様の恒等式「$${S+ΔS≡I+ΔI}$$」が得られる。恒等式「$${S+ΔS≡I+ΔI}$$」から直接的に解釈できるのは、貯蓄(SまたはS+ΔS)の金額の決定要因(determinant)は、投資(I)及び追加的な投資(ΔI)ということである。従って、貯蓄(S)の金額や平均貯蓄性向(APS)を決定するのは、あくまでも投資(I)及び追加的な投資(ΔI)の金額である。
また、基本的な恒等式である国民所得(Y)≡消費(C)+貯蓄(S)に従えば、仮に倹約により消費(ΔC)を削減したとしても、それと同額で国民所得(ΔY)が減少することから、貯蓄(S)自体は不変である。なぜなら消費(ΔC)を削減すれば、ΔC分、総需要が減少し、消費財の売手(供給側)の国民所得(Y)もΔC分、減少するからである。従って、国民所得(Y)≡消費(C)+貯蓄(S)との恒等式が、国民所得(Y−ΔC)≡消費(C−ΔC)+貯蓄(S)と縮小・変形されるだけであり、貯蓄(S)自体は不変である。論理的に考えれば自明のことであるのに、人間の思考の枠を狭める旧来のパラダイムの恐ろしい点である。
ここで一つの実証データを示す。グラフ5は、世界銀行のデータバンクからダウンロードした日本と中国の対GDP粗貯蓄率と粗投資率(1970年-2016年)をグラフ化したものである。1980年代までは両国の粗貯蓄率、粗投資率は共に30%から40%という比較的高い水準にあった。1990年代以降、日本の粗貯蓄率と粗投資率は相関関係を維持しつつ、共に20%台前半にまで低下した。他方、中国は2000年代以降、粗貯蓄率と粗投資率は相関関係を維持しつつ、共に急速に上昇した。特に、リーマン・ショックを契機とする世界金融危機後、中国政府は年間で実質8%成長を維持する「保八」を合言葉として、2008年11月に4兆元(当時の為替レートで57兆円)もの公共投資を実施した。その結果、ピーク時の2010年には中国の対GDP粗貯蓄率51.8%、粗投資率47.6%という驚異的な数字を記録した。
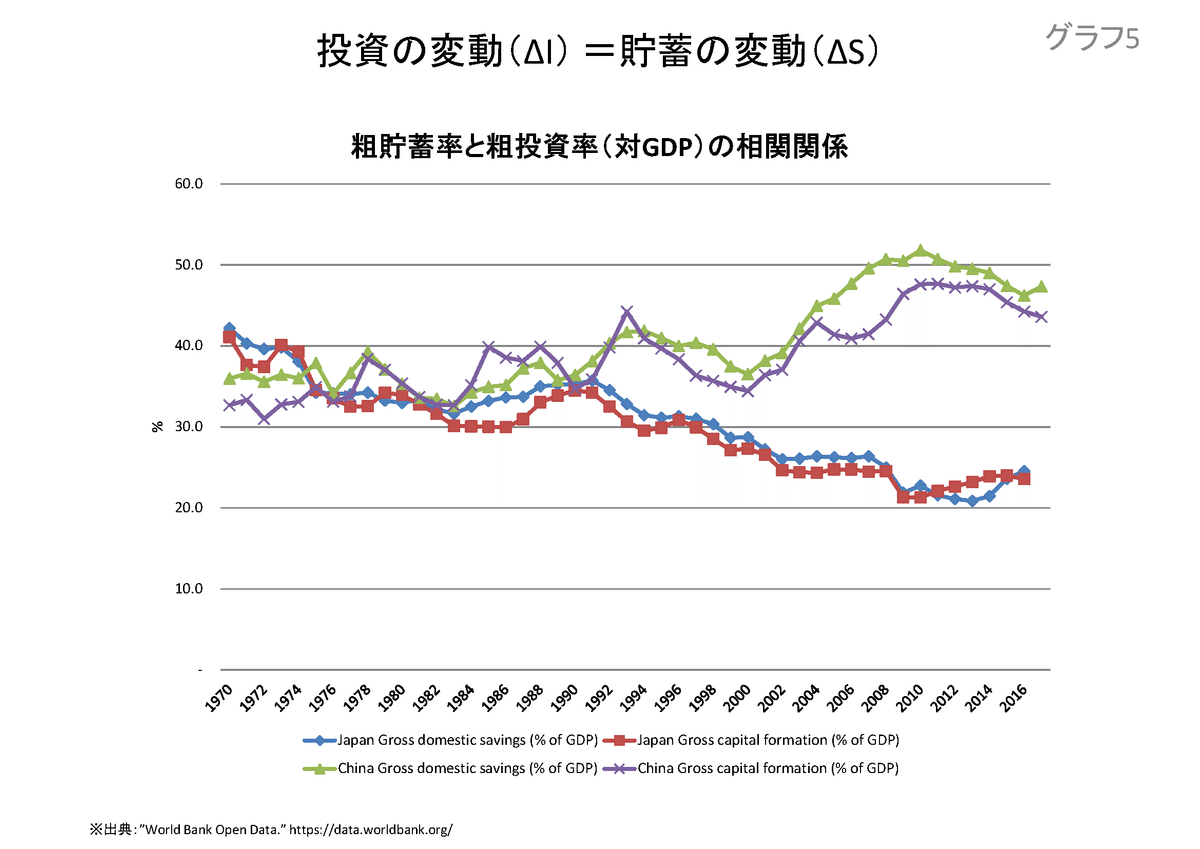
2010年代以降、訪日した中国人観光客が「爆買い」する様子は記憶に新しい。2000年代以降、中国人民がリーマン・ショックを契機として限界消費性向(c)を抑えて倹約に励み、限界貯蓄性向(s=1-c)を国民所得(Y)の50%以上にまで上昇させたとは常識的には考え難い。むしろ上記の命題「事後的(ex-post)に常に必ず投資(I')自体がそれと同額の貯蓄(S≒資本蓄積ΔK)を生み出す」ことが実証データとして確認されたものと解釈すべきと考える。
6-4. 実体的資本蓄積(ΔKs)による国民所得(Y)の拡大再生産
資本の拡大再生産プロセス
こうして貯蓄(S)フローから資本(K)ストックへの変換プロセスを複式簿記の仕訳のロジックで具体的な金額で算定した後、翌期(t+1期)の期首資本(国富)ストック($${K_{t+1}=K_t+ΔK_t}$$)、すなわち{当期首資本(国富)ストック($${K_t}$$)+当期(t期)の実体的資本蓄積($${ΔKs_t}$$)}に当期(t期)の$${β_t}$$(資本/所得比率)の逆数を乗ずると、拡大再生産による翌期の国民所得($${Y_{t+1}}$$)が算定される。
翌期(t+1期)の国民所得($${Y_{t+1}}$$)=翌期首資本(国富)ストック$${(K_t+ΔKs_t)/β_t}$$
={当期首資本(国富)ストック($${K_t}$$)+当期(t期)の実体的資本蓄積($${ΔKs_t}$$)}$${/β_t}$$
Kt: t期首の資本、ΔKst: t期の実体的資本蓄積、Yt: t期の国民所得(償却後可処分所得)、βt: t期の資本/所得比率
【図表16】付加価値生産サイクルにおける「国民所得方程式」

資本の拡大再生産による「国民所得方程式(National Income Equation)」
特に、翌期の国民所得($${Y_{t+1}}$$)=$${(K_t+ΔKs_t)/β_t}$$という数式は、付加価値生産サイクルを経て蓄積された期末資本(国富)ストック($${K_t+ΔKs_t}$$)が翌期に生み出す国民所得($${Y_{t+1}}$$)の拡大再生産を具体的な数値で予測することができる。本稿では、これを資本の拡大再生産による「国民所得方程式(National Income Equation)」と呼ぶ。
こうして付加価値生産サイクルにおいて、フロー変数であるGDP(国内総生産)→国民所得(Yt)→貯蓄(St)が資本ストック($${K_t+ΔKs_t}$$)に変換された後、翌期の国民所得$${(Y_{t+1})=(K_t+ΔKs_t)/β_t}$$に至る拡大再生産の全てのプロセスについて、SNA上の会計恒等式(Accounting Identity)と共に、この「国民所得方程式」を組み合わせるにより、具体的に測定可能(observable)な金額で表すことが可能となる。但し、実際には、4.調整勘定における当期(t期)の再評価による資本蓄積($${ΔKv_t}$$)、具体的には資産価格のキャピタルゲイン/ロスも翌期首の資本(国富)ストック($${K_{t+1}=K_t+ΔKs_t+ΔKv_t}$$)に影響を与えるので、その点にも留意が必要である。
