ピダハン族はなぜ色の名前を持たず、数や数え方を持たず、複雑な構文を持たないのか? PART2-2
数的能力
OTSとANS(SubitizingとEstimation)
アカルキュリアのくだりで触れたとおり、乳児にも認められる基本的な数量表現システムとしてOTS(Object Tracking System)とANS(Approximate Number System)の二つがあり、そのような能力は多くの動物種にも認められることから、個体発生的のみならず、系統発生的にも共有された長い進化の歴史を持つと考えられている。この二つのシステムはグッピーにもそなわっていること、つまり硬骨魚類にまで遡ることを示唆する研究もある。従ってその二つのシステムの存在を仮定する場合、それらはピダハン族にもそなわっている。それゆえにOTS(別名ではParallel Individuation Systemとも呼ばれる)に基づくSubitizing(およそ4以下の項目を数えることなく迅速かつ正確に認識)とANS(別名ではAnalogue Magnitude Systemとも呼ばれる)に基づく数量のEstimation(数量が大きくなるほど精度が下がるおおよその推定)が可能であり、それらは文化的学習を通じて記号的数表現・数的操作能力を獲得するにあたっての基盤を提供するとされる。
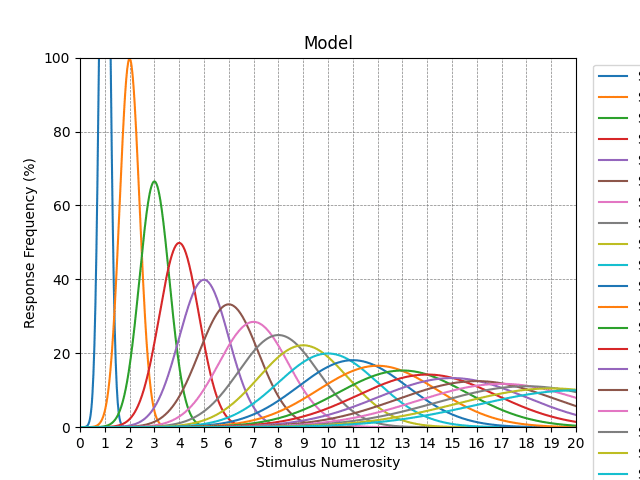
このような2システム仮説、すなわち3~4以下の少数はOTS(PIS)によって、それを超える多数はANS(AMS)によって表現されるという見方が支持される一方、脳における非記号的数量表現は3~4以下も含めて、すべてANSのみに基づいている(OTSはあくまで物理的実体に紐付けられた個体識別であって、抽象的な集合の基数性を表現してはいない)という1システム仮説もあるが、近年では(少なくとも純粋な)1システム仮説を否定する行動学的・神経生理学的な実験研究が多く、それを踏まえた上で、両システムのハイブリッドな見方も提起されている。この見方によれば、3~4以下の少数の対象の場合、脳がそれらを個々に符号化・追跡することが可能であり、従ってOTSによって処理されるが、多数の集合の場合、脳がそれらを個々に符号化・追跡できる限界を超えるゆえに、ANSによって要約的な数の大きさとして表現される。つまり基本的には少数か多数かによって、それぞれのシステムが使い分けられる。とはいえ3~4以下であっても、たとえば対象同士が密に寄り集まりすぎて個々の区別がつきにくい場合、あるいは注意や作業記憶のリソースが他のタスクに割かれていて十分に利用できない場合、その少数は多数と同様にANSによって概数的に表現される。後者の場合を日常的な例で言えば、居酒屋において美味しい食事に集中している場合、テーブルの上の料理が二皿か三皿か四皿なのかを正確に認識しているが、会話に集中して食事が疎かになっている場合、おおよそ三皿くらいという曖昧な認識になっているといった感じだろう。ただしこのハイブリッド仮説と似たような見方をとりながらも、単一のシステムによる統一的説明を試みる立場もある。その説によれば、Subitizingは対象の固定容量(およそ4個以下)によって駆動されるのではなく、視覚的に利用可能な情報量に柔軟に対応して、それを効率的に表現する(少数の対象であっても一瞬しか目にできない場合、不正確になるなど)。そもそも生物は野生の世界において、より頻繁に遭遇する少数の対象の表現に優れており、正確な表現の利点と感覚入力を処理するコストとのトレードオフ、ひいては情報処理能力の限界もある。仮にその限界が厳格である場合、限界より下の少数と限界より上の多数との間に(ある程度の)不連続性が生じて、単一のシステムであっても、多数の表現は厳密性から近似性へと遷移するという。
OTSの神経基盤はあまりよく分かっていないようだが、脳磁図(MEG; Magnetoencephalography)を用いてSubitizing中の脳の活性化パターンを調べた研究では、左右両側の後側頭-頭頂皮質に顕著な活性化が認められており、これは初期視覚処理と物体認識に関与する腹側視覚経路の反映とされる。またfMRIを用いてSubitizingにおける神経相関を調べた研究では、腹側注意ネットワークに属する右側頭-頭頂接合部(rTPJ)の少数(3以下の対象)に対する選択的活性化、および注意負荷に応じた変調が認められており、このrTPJは刺激駆動型注意(顕著な、または予期せぬ感覚的事象に誘引されるボトムアップ型の注意)に関与する領域と見なされている。関連する知見として、複数の視覚的物体を知覚する際、下頭頂間溝がまず4前後の対象を空間的位置に基づいて個体化する(個々の図を地から区別する)のに対して、上頭頂間溝および高次視覚野の外側後頭複合体(lateral occipital complex; LOC)は対象の詳細を識別する(物体表象の解像度を上げて精緻化する)ことに関与しており、物体の複雑さや精緻化の要求が増すにつれて、処理資源の制約により、視覚性短期記憶に保存される物体数が減少するという見方がある。この容量限度の可変性については、列挙課題(寸時提示される図形の数を答える)と視覚性短期記憶課題(同じ図形を用いてどの図形の傾きが変わったかを寸時提示で判断する)における正確性および脳の活性化を比較した結果、列挙課題(数を判断するだけでいいので、対象の識別は低精度で構わない)の方が視覚性短期記憶課題(傾きの変化を判断しなければならないので、対象の高精度の識別が必要)よりも正確に処理できる容量が多く、後頭頂葉の同じ領域(LIP野)の活性化がそれを反映していた(容量限度は列挙課題では3~4項目だが、視覚性短期記憶課題では2~3項目)という研究もあり、この結果は、物体認知と視覚性短期記憶が神経資源を共有しており、課題や文脈に応じた対象の顕著性(目立ちやすさ)や優先度によって、それを識別する精度が変わり、低い特徴分解能で済む場合は多くの項目、高い特徴分解能が必要な場合はより少ない項目を表現できることを示唆している。これらから、SubitizingはOTS(物体追跡システム)に密接に関連すると目されているとおり、やはり数量に特化しているというよりも、対象の個体化に基づくところが大きいようだ。
ANSの神経基盤としては、背側視覚経路に属する後頭頂葉の、とりわけ頭頂間溝(IPS)が主に関与していると見なされており、IPSは特定の量的パラメーターに特異的に活性化するのではなく、数と大きさ、数と位置などで重複を示すことから、数を符号化する神経細胞とその他の量的表現を担う神経細胞は混在して分布している(異なる量的表現の両方に反応する神経細胞もある)ことが示唆されている。それらの神経集団は刺激に応じて変調する地形図のように組織化されて、言わば神経地図を形成しており、たとえば数と大きさの場合、それぞれに対する反応の特性は異なるが空間的分布はほぼ重なっていることから(ただし数は右半球優位、大きさはより両側性)、その重複が汎化された数量表現を可能にしていることも推測されている。ANSに基づく数量知覚・認知についてまとめた最近の総説によれば、中脳の上丘や間脳の視床のような皮質下領域、一次視覚野に投射する視床後部の外側膝状核なども粗い数量処理に関与している可能性があり、そこから二次視覚野や三次視覚野を介して、背側視覚経路とIPS近傍からなる後頭頂皮質へと処理が続き、感覚入力から数量の情報が抽出される。そして数量のEstimation(推定)に関与するIPSの下位領域としてLIP野(外側頭頂間溝野)とVIP野(腹側頭頂間溝野)があり、人間と相同であると類推されるサルの研究から、LIP野はソロバンのように数の合計を表現する総和メカニズム(数が増えるにつれて神経細胞群の発火率も増える)、VIP野は選好される数とその他の数との比率に応じた表現をする数選択性メカニズム(神経細胞群は特定の数に同調するだけではなく、それとの比に応じて他の数に対する反応も調整するので、6と7のような近接した数よりも6と17のような離れた数の方が区別しやすい距離効果、4対5のような小さな数同士の方が44対45のような大きな数同士よりも区別しやすいサイズ効果が生じる)に関与している可能性がある。さらにIPSは前頭前皮質(PFC)の一部と強く相互接続して、前頭-頭頂ネットワークを形成しており、PFCにも数選択性の神経細胞が存在するが、PFCの方が反応が遅く、感覚入力に非依存的かつ離散的な数値に特化しているようであることから、PFCではより抽象的な数の一般化が行われていることが示唆される。
OTSとANSとの神経基盤を比較する研究もある。生後半年強の乳児を対象としたERP研究(知覚・認知処理に伴って発生する事象関連電位と呼ばれる脳の電気生理学的反応を計測する手法)では、Subitizing範囲(1・2・3個のドットを使った刺激)の場合、提示される数に応じて後頭-側頭部に反応が見られた一方、より多数の範囲(8・16・32個のドットを使った刺激)の場合、提示される数間の比率に応じて、後頭頂部により遅い反応が見られた。これはSubitizing範囲は知覚的な処理、大きな数量はより認知的な処理に依存していることを示唆しているかもしれない。またfNIRS研究(近赤外光を投射して脳活動に伴う血行動態を計測する手法)では、画面上のドットを見てその数を答える課題において、数の大小を問わず後頭-頭頂領域にやや右半球優位の活性化が見られたが、Subitizing範囲内の方がやや反応が早く、さらにSubitizing範囲を超えると両側IPS(特に右側)に急激な活動上昇が認められた。この結果から、Subitizingでは刺激駆動型注意に関与するrTPJの活性化が見られるという前出の先行研究を踏まえて、OTSに基づくSubitizingはEstimation(推定)を抑制する一方、注意の限界を超えるとその抑制が外れて、ANSによるEstimation(推定)が働くようになるという推測もなされた。その一方、数に反応する神経地図の研究を発展させて、皮質上の数性地図において、小さな数に対する選好から大きな数に対する選好が連続的に表現されていること、すなわち少数に対するSubitizingとそれを超えるEstimation(推定)に明確な区分がない可能性を示したうえで、やはりそれらは単一のシステムによるものであることを示唆する研究もある。そのような数性地図はIPSを含む頭頂皮質のみならず、側頭-後頭皮質、後頭-頭頂皮質、上前頭皮質にもあり、それらが地図ネットワークを形成している。さらにそれらの数性地図は、視覚野の視野地図(網膜像と対応する)、聴覚野の周波数地図(蝸牛における特定の周波数に対する選択的反応と対応する)、体性感覚野および運動野の体部位再現地図(各身体部位と対応する)などと類似しており、たとえば視覚野では周辺視野よりも中心視野の刺激に対して、より多くの神経細胞群がより鋭い同調性をもって反応するのと同様に、小さな数に同調する神経細胞群の方が割合が多く、ひいては広い面積を占める。そうした神経細胞の同調特性や割合の違いによって、Subitizingとそれを超えるEstimation(推定)との間に、急峻な精度の違いが生じるという。また別のfMRI研究では、提示刺激は1~5個のドットを用いたのでほぼSubitizing範囲ながら、非記号的な数量処理の際、右半球優位のものとして、後頭領域から頭頂領域にかけて物体位置符号化・総和符号化・数選択性符号化の順に活性化の勾配が認められること、また後頭領域は知覚刺激に依存して活性化するが、頭頂領域は課題の性質によって活性化が左右されることが示唆されており、やはり背側視覚経路に沿った段階的な処理を支持している。
こうした知見から、OTSとANS(あるいはSubitizingとEstimation)がそれぞれ分離したシステム(あるいはメカニズム)なのかは定かではないものの、次のような数量知覚・認知の概観が導かれる。(1)皮質下の早期処理から、後頭-頭頂の背側視覚経路を上るにつれて、知覚的な段階からより認知的な段階へと進行する勾配があり、それがさらに頭頂-前頭ネットワークにも繋がっていく。(2)後頭頂領域(特にIPS近傍)が数量の中核的な表現に関与している。(3)少数を把握するSubitizingの場合、おそらく初期視覚野における物体知覚やrTPJによる刺激駆動型注意がそれを深く支えている。(4)その一方で多数の項目の場合、それらを個々に同時識別できるような知覚表現・注意資源がないので、おおよその数量という要約的なEstimation(推定)になる。(5)またSubitizingの際、課題の難度や対象の複雑さによって、視覚性短期記憶の限界が生じるゆえに、精度や容量が下がることもある。
ピダハン族の場合、単純なマッチング課題であっても、3を超えると成績が悪くなったこと、「hói」「hoí」「baàgiso」という三つの用語の意味を調べる課題においても、条件の違いにより非常にまちまちな推定を行っていたこと、短期記憶が要求される課題の成績が特に悪化したことから、上記のような神経表現・神経ネットワークがあまり発達していない可能性が高いだろう。通常成人はSubitizing範囲が4までのところ、ディスカルキュリアの人は3までのことが多く、ディスカルキュリアの場合、IPSの感受性の低さ、およびIPSとその他の脳領域との機能的結合性の低さが指摘されていることから、ピダハン族の場合もおそらく、初期視覚野の知覚的段階よりも、IPS近傍および頭頂-前頭ネットワークなどの認知的段階における発達不足が窺われる。
神経心理学的研究も参考になる。大脳皮質基底核変性症(Corticobasal Degeneration; CBD)、あるいはそのCBDを代表的要因とするより広い臨床単位の、大脳皮質基底核症候群(Corticobasal Syndrome; CBS)の患者においては、しばしば頭頂または頭頂-前頭領域の萎縮が起こるが、それと関連して数的障害を呈するようになり、Subitizingが困難になったり、(おそらくANSが劣化して)距離効果やサイズ効果が生じなくなったりする事例が報告されている。また興味深いことに、そのCBSまたは後部皮質萎縮症(Posterior Cortical Atrophy; PCA)における後側頭-頭頂領域の萎縮に関連して、基数的な量化詞(「三つの」などの正確な基数表現)の理解障害が生じること、また行動障害型前頭側頭型認知症(behavioral variant frontotemporal dementia; bvFTD)においても、吻側前頭前野の疾患や実行制御障害に関連して、単純な知覚論理形式に依存する量化詞(「いくらかの」などの具体的な数量を含まない表現)、Majority量化詞(「少なくとも半分の」などの集合の過半以上の表現)の理解障害が生じることが報告されており、これらは大規模な前頭-頭頂ネットワークが量化詞(数量詞)の理解に重要な役割を果たしていること、大脳基底核の疾患が実行機能(ワーキングメモリや戦略的比較など)に関与する前頭-線条体ループ回路を阻害することを示唆している。CBS患者は一週間の日数やフィートあたりのインチ数なども理解できなくなるようで、これはアカルキュリアのくだりで取り上げた患者C.G.も一週間を「4日」と答えたこと、その損傷部位が左前頭-頭頂領域だったことを思い出させる。そして上記の知見は言うまでもなく、ピダハン族の言語には明確な量化詞(数量詞)が存在しないというエヴェレットの主張も思い出させるだろう。ちなみにこの量化詞の理解障害は失語症を伴わない患者において認められており、従って言語性ではなく、数量認知やワーキングメモリ(短期記憶の情報を維持・操作する能力)などに関する障害と推測されるが、ピダハン族の場合、そうした認知能力が発達不足であり、またその発達を強いられない文化圏・環境に暮らしているがゆえに、明確な量化詞がその言語において必要ではなく、ひいては発生しないという理路になるだろう。
SubitizingとCounting
さらにピダハン族の場合、数詞やアラビア数字などの数的記号を持たず、おそらくCounting(計数)ができない。これについてはまず第一に、数量知覚・認知における右半球優位という知見が示唆に富んでいる。たとえば生後6ヶ月の乳児を対象としたfNIRS(機能的近赤外線分光法)研究では、数に対する右頭頂領域に特化した活性化が報告されている。就学前の幼児を対象としたfMRI研究においても、数量表現に対して、右IPSの方が左IPSよりも鋭い神経同調性を示すこと、すなわち右半球の優位および早期成熟が報告されている。これらの研究の被験者は言語学習以前の乳児、記号的数体系習得以前の幼児であり、発達早期において数量処理は右半球に多くを依存していることを示唆している。その一方でそれ以降の年齢、就学後の6~14歳児を対象としたfMRI研究では、記号的数値の皮質表現における発達的変化を調べた結果、年齢と左IPSの活性化との間に相関が認められた。成人を対象としたfMRI研究においても、数の近似的なEstimation(推定)の場合、右頭頂-前頭ネットワークが活性化されたのに対して、正確なCounting(計数)の場合、それに加えて左頭頂-前頭の相同領域、および両側運動前野(数え上げに伴う発声や指の動きを反映している可能性がある)も活性化されたことが報告されている。また非記号的な数(量や大きさ)の処理は右IPSの活性化と相関する一方、記号的な数の処理は左下頭頂小葉の活性化と相関するという報告もある。これらの研究から、非記号的かつ大まかな数量処理はおそらく右半球優位であり、計数や記号的数体系を習得するにつれて、左半球優位の記号的かつ正確な数的処理も発達していくことが示唆される。これは大半の人々にとって、左が言語優位半球であることに関係がありそうだが、Counting(計数)の際、両側の頭頂-前頭領域に活性化が認められるという上記の知見から、記号的数処理の際にも、右頭頂領域は重要な役割を果たしているものと考えられる。
次いでこの点に関しても、神経心理学的研究が参考になるだろう。41名の脳損傷患者を標本として、ボクセルベース・モルフォメトリー(voxel-based morphometry; VBM)と呼ばれる全脳の灰白質・白質の体積や密度を解析する手法により、視覚的なEnumeration(数え上げ)において、Subitizing範囲(1~3)とそれを超えるCounting範囲(6~8)における障害の神経相関を比較した研究によれば、両範囲の障害には重複する脳領域も多いが、同名半盲や視覚性注意障害の影響を除外してもなお、それぞれ別々に分離可能な相関も認められるという。(1)Subitizing障害とCounting障害に共通して、両側視覚野および高次の後頭-頭頂領域(両側の中後頭・上後頭領域、IPSを含む頭頂領域、楔部)と前方・上方・内側の前頭皮質からなる病変ネットワーク、さらに視放線へと伸びる脳梁幹(脳梁体部)後部両側領域の病変との相関があり、これは外線条領域(視覚前野)と前頭-頭頂領域が視覚的数え上げで活性化されるという既存の知見と一致している。(2)Subitizingの精度低下に特に関連するものとして、視覚的物体処理を担うとされる外側後頭複合体(LOC)を含む左後頭領域(初期視覚野・左中後頭回・左上後頭回)の灰白質の減少、さらに右後頭領域(右楔部・右上後頭回)、右前頭領域(右上内側回および右中前頭回)の病変がある。(3)Countingの精度低下に特に関連するものとして、前頭極の小領域の病変、脳梁幹(脳梁体部)後部の白質損傷があり、前頭極の損傷は、項目の継続的な数え上げや視覚的注意の誘導に関する障害を反映している可能性がある(ただしSubitizing障害にもいくらか関連しているかもしれない)。(4)Subitizingに重い障害がある場合、Countingの精度も低く、両範囲において非常に不正確だが、そのような4人の重篤患者を除いた場合、左IPS水平部の灰白質の減少がCounting範囲の成績悪化と選択的に相関している。(5)Subitizing範囲でも数の増加に伴って反応時間の大きな増加が認められる場合、1~3項目でさえも並列的に寸時処理できず、直列的に順次Countingを行っていると推測されるが、そうした患者は、鳥距溝・楔部・楔前部からなる両側の内側後頭の広い領域(右側がより顕著)に灰白質減少が認められる。(6)なかでも楔前部は同時失認(Simultanagnosia)の研究において、大局的な視覚情報処理に関与していることが報告されており、同時失認患者は楔前部の活性化が低く、Subitizingの劣化が認められることも多いが、これはSubitizing障害と大局的視覚処理障害との関連性を示唆しており、Subitizing障害は細部の刺激を平行して理解する能力の低さによる可能性がある(同時失認との関連については少し後で述べる)。(7)視野障害(視覚的な探索や走査に時間がかかる)患者を除いた場合でも、Subitizing範囲の反応時間の遅さ(つまりその範囲でもCountingを行っている可能性)は、左側のローランド弁蓋部(島皮質前部を覆う領域)および中心前回の広い領域の損傷、さらに高次後頭領域(右側の上後頭回や楔部の近傍)、左視床、左下側頭回、中帯状回、下前頭回の灰白質の減少と相関しており、とりわけ中心前回の後部は一次運動野における手と身体の表現に関与していることから、Subitizingは数の学習における指数えとの関連性があるのかもしれない。(8)Subitizingは保たれているが、より大きな数のCountingが損なわれている場合、ワーキングメモリ(短期記憶の情報を維持および操作する能力)・実行機能・計算機能などの障害が示唆される(これらの能力は実行中の合計の維持や既に数えた項目を追跡することに関わる)。(9)SubitizingとCountingの反応時間の勾配には相関がないことから、両者は分離できることが示唆される一方、SubitizingとCountingの両範囲を左IPSが支えている。
以上からSubitizingとCountingともに、両側の後頭から頭頂領域へと流れる背側視覚経路、左IPS、そして頭頂から前頭領域にかけてのネットワークが関与していることが窺われる。前述のとおり左IPSは右IPSよりも記号的数処理に偏向している可能性が高いことから、すべての範囲にわたる数え上げに重要な役割を果たしているのだろう。また特にSubitizingにおいて重要な領域として、外側後頭複合体(LOC)を含む左後頭領域、右側がより優位な内側後頭領域(鳥距溝・楔部・楔前部)、左側の中心前回近傍があり、それぞれLOCは物体認知、楔前部は大局的な視覚処理、中心前回近傍は指数えと関連する運動性の表現に関連しているものと推測される。その一方、特にCounting(計数)において重要な領域として、前頭極を含む前頭領域、左IPSの水平部があり、前頭領域または前頭-頭頂ネットワークはワーキングメモリや実行機能や計算機能、左IPSは正確な数の表現に関わっているようだ。そして最後に、Subitizingの重度の障害はCountingの精度も低下させることから、前者が後者の土台の一部になっている可能性も示唆される(この点に関しては前出の、OTSが整数概念・基数表現・計数アルゴリズムなどを獲得する基礎になっているという仮説も参照)。
このような概観はその他の症例研究によっても補強される。主として右側もしくは両側の後頭頂・後頭・後側頭領域の病変、あるいは大脳基底核の尾状核に異常が認められる5人の同時失認患者を対象とした実験研究(スクリーンに表示された1~6個の長方形の数を答える)では、4以上のCounting(計数)が障害されているにもかかわらず、2~3以下のSubitizingは比較的保たれていたという報告がある。同時失認とは、個々の物体の知覚、視覚的情景の部分的な認識は保たれている一方、複数の物体を同時に知覚すること、視覚的情景を全体として認識することに困難をきたす症状であり、目の前に車が何台も通っていることは分かっていても、一台ずつしか見ることができなかったり、映画のスクリーンの断片や細部にばかり注目が囚われて、全体の意味を把握することができなかったりする。この同時失認では視覚情報処理において、(1)対象の同一性を識別する「何」システムと(2)対象の空間的位置を識別する「どこ」システムとの統合が損なわれている可能性があり、その結果、対象の同一性情報が空間的位置情報から切り離されてしまうかもしれず、この実験研究の場合、スクリーンに表示された長方形が大きさ・形・色などの違いがない同一の図形であったがゆえに、患者は直列的に一つずつ対象を数える場合、ターゲットの長方形同士を区別して追跡できず、ひいてはそれぞれの空間的位置を定位できないゆえに、見落としが生じてしまったり、同じものを何度も数えてしまったりしたものと推測された(ただし同時失認がどのようなメカニズムの障害なのかについては諸説ある)。そしてCounting(計数)は障害されていたにもかかわらず、2~3項目以下の数量化はそれなりに正確だったことから、Subitizingは直列的な計数(一つずつ順番に対象を数え上げていくこと)とは別の、並列的な処理であることが示唆された。とはいえ通常の成人よりもSubitizing範囲が狭かったことから、そちらも無傷ではない可能性が高い。この実験でもうひとつ興味深いのは、Subitizing範囲を超える4~6個の長方形であっても、それがサイコロの目と同様の規則正しい配置になっている条件の場合、その数を正答できる患者もいたことだ。対照群の健常者もこのサイコロ配置の場合、200ミリ秒の寸時提示であっても間違いを犯さなかったので、これは計数とは別のパターン認識によるものと推測された(見慣れたパターンが数とセットで記憶されているのだろう)。
上段の研究を行ったドゥアンヌとコーエンはその他の著者らと共に、Subitizingに障害があると思しき患者LECの症例も報告している。LECは3以下でも項目の数が増えるごとに、それ以上の数を数える時と同じように反応時間が増加していき、また刺激を一瞬フラッシュさせるだけの条件では、3以下の数でも誤りを犯した。つまり3以下の数でもおそらく直列的な数え上げを行っており、なおかつ、並列的な処理であれば把握できるはずの、寸時提示でも少数の知覚に困難を呈した。これはSubitizingに障害があることを示唆するが、興味深いことに、LECには左IPS近傍の皮質病変、加えて右後頭領域の出血もあり、同時失認およびゲスルトマン症候群を呈していた。ただしLECはSubitizing範囲を超えるCounting(計数)にも障害が認められており、また概数比較課題でも障害が認められたことから、ANSも含む数量表現が広範に損なわれている可能性が高い。これと類似した症例として、同様に左IPSに病変があり、一次性アカルキュリア(および当初は軽度の失書)を呈した患者ADにおいても、Subitizing範囲の縮小(2まで)、Counting(計数)の障害、ANSにもいくらかの障害が認められている。
5人の同時失認患者の研究に似て、3~4までのSubitizingは完璧に保たれている一方、その範囲以上のCounting(計数)に重大な障害(数えるのが遅く、正確性も低い)が認められたMHという患者も報告されている。このMHはCounting(計数)の障害に加えて、実験者が最大9個のブロックを順々に叩くのを見た後、それを同じ順番で叩かなければならないテストにおいて、2個までしか正しく叩けないという、顕著な視空間性短期記憶の障害を示した(健常者の平均は5~6個)。さらに紙の上の数十個の星マークを一つ残らずペンの頭で叩いていくテストにおいては、繰り返し同じ星を叩いてしまう回数が非常に多く、空間的位置情報の符号化に障害があることが示唆された。興味深いことに、MHは星マーク課題と類似した別の実験において、やはり同じ対象を誤って再訪問してしまう回数が異常に多かったが、にもかかわらず、それが再訪問であることに自分で気づくことができた。これはつい誤りを犯してしまうが、その誤りを検出するモニタリングは機能していることを示している。このMHの場合、基本的な数的理解力には問題がなく、音を数える能力は保たれていたことから、視空間的な障害の可能性が高く、そのうえ視覚的なCounting(計数)の際でも、対象を一つずつ指でタップすることを強いられた条件では、Subitizing範囲を超えてもかなり成績が改善した。これは運動記憶系の補助効果か、あるいは同時的ではなく逐次的な視空間情報の利用は可能であるか、いずれかの可能性があるという(触覚的な数え上げの可能性もある気がするが)。なお病変部位に関しては、皮質下は両側大脳基底核のレンズ核および尾状核前部の萎縮、皮質では両側の後頭頂領域、それも左側(後頭-頭頂の境界領域およびIPSを含む)でより顕著だった。
ピダハン族はその視知覚や視覚認知において、明らかに同時失認のような障害を呈してはおらず、またマッチング課題において3までは成績が良かったことから、Subitizing能力はそこまで極端に低いわけではない。前出のムンドゥルク族の数詞研究においても、ほぼ正確に用いられるのは1と2だけではあるものの、3と4の用語もそこそこ正確な精度で用いられている。おそらく高度な数的文化を持たない人々はSubitizing範囲が4よりも3に近い程度に留まるのだろうが、それでも現代的に工業化された文化圏の人々と比較して、視知覚という側面には取り立てて不足はないと思われる(アクションゲームはCounting能力を向上させるが、Subitizing能力は向上させないことを示唆する研究も報告されており、また知覚対象に関する知識はワーキングメモリの解像度を向上させるが、一度に取り扱える項目数は増加させないという研究もあることから、Subitizing範囲には臨界期・敏感期があるのかもしれない)。従ってピダハン族の場合、皮質下や後頭皮質の視覚処理よりも、より高次の認知処理、それも非記号的数量よりも、より正確な記号的数量に側性化している左IPSを中心とした神経表現、さらにはIPSから前頭領域へのネットワーク、これらにおける発達不足がやはり推測される。実際、アメリカ中流層の平均年齢3歳の幼児を対象として、数(集合の大きさ)を推定させた実験では、1まで推定できる者、2まで推定できる者、3まで推定できる者、4まで推定できる者などその能力は様々だったが(それ以上の数を暗唱することはできるが、数の意味は推定できる範囲までしか正確には理解していない)、4を超える集合を正しく推定できた者はわずかであり、多くの幼児は自分の推定できる範囲を超えた集合に対しては、すべて同じ数を当てはめたり、無作為に数を当てはめたりする傾向があった。この数的認知能力が発達途上にある幼児たちの特徴には明らかに、ピダハン族やムンドゥルク族との類似性が認められる。言語進化の観点からも、計数原理が広く文化的に構築されるまでは、人間の言語には1~3または4個の物体の集合を表す形態素しか存在せず、それらも元々は量化詞だったという言語学者の見解があり、数的文化を持たない場合、正確な数の理解には人間のSubitizing能力が反映されるに留まるのだろう。
以上はSubitizingがCounting(計数)の土台の一部になっている可能性、左IPSおよび前頭領域の損傷がCounting(計数)の障害に深く関連しているという知見から推測されるが、もう一点、非常に推測的ながらも連想されることがある。前頭領域は上述のとおり、頭頂領域とネットワークを形成しながら、計数の際、数えた合計や既に数えた対象を念頭に留めておくこと、つまり短期記憶上の情報を維持・操作するワーキングメモリに深く関わっている可能性があるが、これは左IPSがより記号的数表現に側性化しているという知見も含めて、前出の心的イメージ障害の症例研究における特定の見解を思い出させる。それはすなわち、左頭頂葉損傷の場合、視空間イメージ障害や同時失認に相当するものが、概念レベルの空間において生じる可能性があるという見解であり、念頭において、抽象的な数表現を維持できなかったり、数表現を操作できなかったりすることは、まさに概念レベルでのイメージ障害や同時失認に相当するのではないかとも思える(ただし同時失認は両側の損傷によるものというのが現在では定説のようだ)。
計算・算術
そして計数アルゴリズムや記号的数体系を習得しながら、その概念レベルにおいて数という抽象的表現を維持・操作する高度な能力として、計算や算術と呼ばれるものがあり、ピダハン族はそうした能力にも乏しいことから、それに対応する神経表現や神経回路も発達しないことが推測される。この点に関してはまず、ドゥアンヌらが前世紀末に提唱した数処理のトリプルコード・モデルが大まかな見取り図として参考になるだろう。このモデルによれば、脳内における数処理の際、課題に応じて三つの表現システムによる符号化が用いられる。すなわち、(1)数同士の大小および距離関係の非記号的・前言語的なアナログ表現を担っており、数量の意味的知識を支え、大きさの比較・推定・概算を可能にする量システムによるアナログ的な量または大きさのコード、(2)単語と同様に数字の語彙的・音韻的・統語的な表現を担っており、計数や暗記された算術的事実(九九など)の検索を可能にする言語システムによる言語性コード、(3)数をアラビア数字の文字列として符号化して、数の記号的な認識・操作を可能にする視覚システムによる視覚性アラビア数字コードの三つであり、(1)は両側のIPSを中核とした下頭頂領域、(2)は左側の角回・縁上回・側頭葉などのシルヴィウス溝(外側溝)周囲領域、(3)は両側の下腹側後頭-側頭領域がそれぞれ主に関与すると仮定されている。これらは計算の種類や難度によって異なった相互作用をする。たとえば暗記された一桁の足し算や掛け算の場合、アラビア数字で書かれた式を視覚システムが識別、それを言語システムが言語表現に変換、さらに学習された順序処理を担う大脳基底核および視床を通って暗記知識が自動的に読み上げられるという、左側の皮質-皮質下ループの直接経路を辿る。その一方、そのような自動的処理に頼れない(暗記知識に乏しい引き算や割り算、多桁の複雑な計算などの)場合、式を視覚システムが識別、それを量システムが量表現に変換、その量に対して意味的な操作手続きが実行された後、その結果が言語システムに送られて言語化されるという、間接経路を辿ることになる。もちろん大抵の計算では、この両方の経路が同時に使われる。たとえば多桁の掛け算では、それを単純な部分に分解して暗記知識で対処したのち、その結果を量的な操作で組み合わせたりするだろう。
さらにドゥアンヌらはこの見方に関連して、頭頂葉に以下のような、数処理のための三つの神経回路があることも提唱した。すなわち、(1)中核的な量表現に関与する両側の頭頂間溝(IPS)系、(2)言語性数処理に関与する左角回(lAG)系、(3)空間性および非空間性の注意に関与する後上頭頂小葉(pSPL)系であり、これらは前世紀末から今世紀初頭にかけての、fMRIを用いた神経解剖学的研究の進展を通じて推測されるようになった。もう少し詳しく言えば、(1)のIPS量系回路は頭頂間溝水平部(hIPS)を主要部位としており、この部位は空間地図や数直線に類似した非言語的な数量表現を担って、数の大きさや数同士の近接関係を直感する基礎となり、入力形式(アラビア数字・数詞・ドットなど)に依存せずに、それが表す抽象的な数量的意味を符号化する。また単に数的記号を読む時よりも、量的表現や数的操作が必要とされる場合(数のおおよその推定をしたり、大小の比較をしたり、引き算をしたりする際)により活性化する。(2)のlAG言語系回路は左hIPSの後下方の外側にあり、関係領域と連携しながら、量的表現そのものではなく、暗記された掛け算を想起する際など、数の言語的符号化が強く要求される場合にのみ、その度合いに応じて数処理に寄与する。従って、純粋な量的表現の操作を必要とする計算(引き算や割り算や複雑な計算)よりも、言語性記憶に保存された算術的事実(暗記された九九や一桁の足し算)を検索する場合により活性化する。(3)のpSPL注意系回路は両側hIPSの上後方に位置して、多くの場合、内側の楔前部へと拡張しており、比較・近似・二桁の引き算・計数などの際に活性化する。しかしこの領域は明らかに数処理に特異的ではなく、対象へ手を伸ばす・把持・指差し・視線または注意の定位・心的回転・空間性ワーキングメモリなどに関与していることから、空間に類似した心的次元、たとえば内的な「数直線」のような準空間的表現において、外空間において位置を選択するのと同様に、特定の数に注意を向けることに関与している可能性がある。これら三つの神経回路の機能的特徴や相互分離は、それぞれの領域の脳損傷患者を対象とした神経心理学的研究を通じても総じて支持、またはそれなりに示唆されている(たとえばアカルキュリアのくだりでも引用した文献やその他を参照)。
こうした概観はその後の研究を通じて掘り下げられている。たとえば数と計算に関するfMRI研究の56の実験データをメタ分析した論文では、後頭頂葉(IPSを境にして上下の頭頂小葉に分けられる領域)が最も高い活性化を示した部位の一つだったこと、下腹側後頭-側頭部にある左紡錘状回が視覚性数字認知に関与している可能性が高いことなど、トリプルコード・モデル(IPSが数量表現の中核であり、下腹側後頭-側頭部が視覚性アラビア数字コードを担う)を少なからず支持するような結果が出ている。ただし計算の際に活性化される前頭-頭頂ネットワークの各部において、足し算は左側性、引き算は両側性ないし左側性だが、掛け算はおおよそ右側性という結果が出ており、これは掛け算では左角回を主とした言語系の算術的事実検索に依存することが多いという、トリプルコード・モデルの予測とは相反する(四則演算それぞれの違いをメタ分析した研究においても、トリプルコード・モデルとの齟齬として、掛け算では右角回および右背側前頭前野が活性化されることが指摘されている)。これについてこのメタ分析では、右角回は目標指向の顕著性表現に関与していることから、問題解決時の視空間的な事実検索に関わっている可能性があるという解釈がなされている(暗算では頭の中で筆算をするように、計算過程を視空間的に思い浮かべることも多いので、そのような知識が呼び出されているのかもしれない)。この点に加えて、算術的情報処理においてワーキングメモリ・注意・認知制御などに関与する前頭前野が重要な役割を果たしていること、その前頭前野の寄与はおそらく、下前頭回は単純な課題、中前頭回はより複雑な手続きや認知的負荷を要求される課題、内側前頭回および上前頭回(特に前頭極)は多くの段階を要する問題を解くための戦略生成といったふうに、課題の難度によって大別されること、その他、背側帯状回・中心前回・島皮質・小脳なども数と計算に関する課題において活性化が認められることから、トリプルコード・モデルの更新が提案された。
より解剖学的・構造的な分析を行った研究もトリプルコード・モデルを概観として踏襲しながら、その修正を提案している。それによればまず、数の大きさに関連した処理は頭頂間溝(IPS)、IPSの後方領域(上頭頂小葉の7A野および7P野)、そして前頭領域の補足運動野・前頭眼野・下前頭回(ブローカ野および腹側前頭前野)を活性化させる。数量表現の中核と見なされるIPS領域以外の、補足運動野は様々な関連処理の支援、前頭眼野は注意制御(眼球運動を制御して視線を操作するのと同様に、内的な注意を調節しているのかもしれない)、下前頭回の特にブローカ野は規則の適用に関与している可能性がある。また言語性の算術的事実検索は左側の角回・縁上回・上側頭回・中側頭回といった言語野、そして長期記憶からの想起に関与する海馬・脳梁膨大後部皮質・腹内側前頭前野を活性化させる。さらに視覚性数字認知に関与する紡錘状回の視覚性数字形状領野(Visual Number Form Area; VNFA)はIPSと接続しており、数字と数の大きさの処理とが結びつけられている。これらの回路は数的認知において、統合された回路網として機能しており、課題の特性によって各々の関与の度合いが変わる。こうした見方に関連して、白質線維路による接続性に焦点を絞った分析では、以下のような連絡が数的認知を支える神経回路網と同定された。すなわち、(1)頭頂領域(IPS・上頭頂小葉・角回・縁上回)と前頭領域(背外側前頭前野・腹内側前頭前野・中心前回・補足運動野・下前頭回)との連絡を担う連合線維(同側の皮質領域間を接続する線維)としては、上縦束によって結ばれる背側経路および外包・最外包によって結ばれる腹側経路があり、(2)それらの領域と大脳基底核や視床との連絡を担う投射線維(皮質領域と皮質外領域を接続する線維)としては、上下方向に走行する放線冠上部や内包があり、(3)数の大きさ処理に関与する左右のIPSの連絡を担う交連線維(左右半球を接続する線維)としては、頭頂葉内側を結びつける脳梁峡部があり、(4)側頭葉内側の海馬はそれらの領域と結合性を持ち、算術的事実検索において重要な役割を果たしている。
トリプルコード・モデルにおける三つの表現システムの個々についても、より詳細な見方が提示されている。活性化尤度推定(Activation Likelihood Estimation; ALE)と呼ばれる脳領域の活性化位置を定位座標上に定量的に合成する手法を用いて、57の神経イメージング研究を定量的にメタ分析した論文によれば、記号的・非記号的な数表現に対する共通の活性化領域を探索した連結分析の結果、両側の下頭頂小葉および楔前部・左上頭頂小葉・右上前頭回がその領域として浮かび上がり、これらが表現形式に依存しない抽象的な数処理を支えている可能性があるが、その一方、記号的な数表現と非記号的な数表現に対する活性化パターンには関連性が認められないことから、むしろ入力形式に依存して異なった処理が行われている可能性も示唆された。そしてその後者を探索した対照分析の結果、まず記号的数処理では、左下頭頂小葉(特に角回)および右下頭頂小葉(特に縁上回)が特異的に活性化しており、なかでもアラビア数字に対しては、左下頭頂小葉に特化した活性化が認められた。この左右両側の下頭頂小葉の活性化は掛け算の際、右角回が活性化するという上述のメタ分析とも一致しており、左側が言語的処理と記号の読み取りに関与する一方、右側は注意過程を担って計算の実行に関与している可能性が推測される。次に非記号的数処理では、右側の上頭頂小葉および楔前部が特異的に活性化しており、上前頭回・内側前頭回・中心前回・島皮質・帯状回などと共に前頭-頭頂ネットワークを形成している。以上から、左頭頂葉の下方は記号的数処理に側性化していること、右頭頂葉は上方が非記号的処理、下方が記号的処理という活性化パターンを持っていることが示唆された。また計算課題などに伴う高次認知処理(ワーキングメモリ・注意制御・反応選択など)の影響をなるべく排して、数表現そのものに対する活性化パターンを抽出すべく、受動的な数刺激のみを分析した結果、記号的刺激では左楔前部および左紡錘状回、非記号的刺激では右楔前部および左上頭頂小葉、さらに左中後頭回の活性化が認められた。非記号的刺激の活性化のクラスターは右頭頂葉の方が大きかった。以上から、記号的数表現は左頭頂葉、非記号的数表現は右頭頂葉のより広い範囲を活性化することも示唆された。この定量的メタ分析では、数量表現システムはIPSのみならず頭頂領域全体に広がっていること、記号的・非記号的それぞれの数処理で左右の側性化の傾向があることが示されており、その点がトリプルコード・モデルと異なる。
上段の定量的メタ分析では、やはり左角回が言語的な数処理に関与していることも示唆されているが、算術における角回の役割については、トリプルコード・モデルの見解のみならず、それ以外の仮説も提起されている。この論点をまとめた総説によれば、その仮説は(1)トリプルコード・モデルの提案した言語性の算術的事実検索、(2)記号-参照の対応付け、(3)注意配分の三つに大別される。まず(1)の算術的事実検索とは、これまでにも述べたとおり、角回が長期記憶として保存された知識を取り出す媒介を担っているという仮説であり、加齢や訓練に伴って、前頭領域および皮質下(大脳基底核や視床)の活性化が減少する一方、左角回およびその周辺領域の活性化が増えるという研究、あるいは反復経頭蓋磁気刺激(rTMS)によって左角回に一時的障害を引き起こした場合、被験者が計算手続きを用いたと報告した問題よりも、暗記知識の検索に頼ったと報告した問題の解答能力が低くなったという研究などに基づいている。これらから、人は算術に習熟するにつれて、手続き的な計算を担う前頭-頭頂(さらには基底核を含む)ネットワークから、暗記知識の検索を担う側頭-頭頂ネットワークにより多くを依存するようになり、その検索には左角回近傍が主に関与していることが示唆される(知識を記憶する初期過程では特に、記憶の符号化を担う海馬が重要な役割を果たすと考えられている)。次に(2)の記号-参照の対応付けとは、角回が記号とその記号が参照する概念との結び付きを支えているという仮説であり、両側の角回が算術以外の、図形-空間問題の訓練後にも活性化が増加するという研究、数学能力が高い人の左角回の活性化は暗記された算術の想起に限定されず、数学記号全般の処理能力と相関しているという研究などに基づいている。さらに加えて、左角回は書き言葉と話し言葉との対応付け、あるいは視覚的な単語とその意味との対応付けにも関与しているという知見もある。これらから、角回は数的情報処理に特異的ではなく、より一般的な記号-参照処理に関与していることが示唆される。最後に(3)の注意配分とは、角回が複雑な手続きが必要な計算よりも、暗記された単純な知識の検索によって活性化するのは、文字どおり注意資源の配分によるものだという仮説であり、角回がデフォルト・モード・ネットワーク(安静状態・受動的状態では活性化が高まる一方、より困難な心的課題に努めて取り組むほどに非活性化を示す大規模な神経ネットワーク)の後方拠点として、記憶検索時に後帯状領域・楔前部、左の海馬傍領域と共に活性化する(その後、検索された情報を操作する過程ではより背側かつ前方の、前部IPSおよび中心後溝が大きく関与する)という研究、さらに角回と縁上回からなる腹側頭頂皮質が(刺激や情報が内発性か外発性かを問わない)ボトムアップ型注意を媒介しており、記憶検索時の想起が確かなほど、顕著な内容を自動的な注意によって捕捉できているゆえに活性化する(その一方、背側頭頂皮質はトップダウン型注意処理を媒介しており、記憶検索時の想起が不確かなほど、それを努めて思い出そうと意識的に注意を向けるゆえに活性化する)という理論などに基づいている。これに関連して、記憶検索それ自体には海馬・海馬傍回・脳梁膨大後部領域などが大きな役割を果たしており、左角回は「仲介役」または「回路遮断器」のように働き、算術中、ボトムアップ的な事実検索とトップダウン的な計算操作との間で注意資源の割り当てや切り換えを調整するという見方もある(つまり頭頂皮質の上方はトップダウン型注意、下方はボトムアップ型注意を担っており、片方が活性化するほどに、もう片方は非活性化するという相互依存関係にある)。これらから、角回は算術処理に特異的ではなく、より一般的な注意資源の配分に主に関与していることが示唆される。以上の三つの仮説は必ずしも相互に排他的ではなく、両立しているかもしれない。たとえば九九の想起といった算術に関する事実検索は、記号-参照の対応付けの一種とも見なせるものであり、記号とそれが参照する意味内容を自動的に結びつける際には、ボトムアップ型注意が主要な役割を果たすとも見なせる。この総説の著者らは、算術における事実検索と計算手続きそれぞれの活性化領域のメタ分析も行っており、その結果、事実検索は左角回と上・中側頭回にまたがる活性化、計算手続きは前頭領域の右帯状回と左下前頭回の活性化と特に関連しており、また両方に共通して両側の下頭頂小葉(左側は上頭頂小葉にも及ぶ)の活性化が浮かび上がったことから、その包括的な機能が何であるにせよ、少なくとも暗記された知識を想起する際、やはり左角回が重要な役割を果たしている可能性が高いことが示唆される。
数字認知については、視覚性数字形状領野(Visual Number Form Area; VNFA)、または単に数字形状領野(Number Form Area; NFA)とも呼ばれるアラビア数字の処理に特化した脳領域を探索するfMRI研究の結果は一貫しておらず(発見を示唆する結果もあれば不在を示唆する結果もある)、現生人類の歴史において、かなり新しい発明である数字体系やアラビア数字に特異的な処理機構が進化を通じて生得的にそなわっているとは考えがたいことから、その存在が疑問視されてもいるが、諸研究を選りすぐって統合したメタ分析では、非常に不十分な証拠ながら、トリプルコード・モデルの予測した両側の紡錘状回ではなく、右側の下側頭回後部(紡錘状回のすぐ近くではある)にその推定位置が収束した(つまりもし仮にNFAが存在するとしたら、それは右後下側頭回に位置する可能性がある)。さらにその推定NFAに加えて、右側の楔前部・前上頭頂小葉・IPSから下頭頂小葉に及ぶ頭頂領域、同じく右側の上前頭回(特に運動前野)・帯状回・下前頭回といった前頭領域、また左側のIPSから下頭頂小葉(特に縁上回)に及ぶ頭頂領域、これらからなる右側優位の「記号的数字処理ネットワーク」が視覚的に提示されたアラビア数字の処理に機能的に特化している可能性も示唆された。ただし推定NFAを電気刺激して一時的に障害を引き起こした結果、アラビア数字のみならずローマ字(つまりアルファベット)の処理も阻害されたことから、この領域はより一般的な記号処理に柔軟に関与している可能性がある。またネットワークという観点では、推定NFAを含む後部下側頭回は前部IPS(および上頭頂小葉の一部)と機能的に結合しており、アラビア数字の受動的処理(記号の視覚的認識)の場合、推定NFAを含む後部下側頭回は前部IPSとボトムアップ型の結合を強く示す一方、算術処理(計算のような高次の数的処理への数字認識の統合)の場合、その逆のトップダウン型の結合を強く示すことも示唆されている。とはいえ神経心理学的研究では、左側の側頭-後頭領域(特に紡錘状回後部)の損傷に起因することが多い純粋失読(読字が選択的に傷害されており、書字や音声言語は基本的に無事)における文字と数字の読みを調査した総説において、その片方が傷害されて片方が無事という事例を明確に示した研究はこれまでに一つもなく、数字の失読と文字の失読との間に強い乖離があるという確固たる証拠はないと述べられている。これは数字認識に特異的な領域は存在せず、あくまで文字と同様の、より汎用的な記号処理機構がその媒介であることを示唆している。あるいは上記のネットワークという観点を踏まえれば、その他の領域との結合性によって、相対的に特化された処理が行われるのかもしれない。この総説では興味深いことに、純粋失読では押し並べて、文字よりも数字の方が障害の程度が軽い傾向があるが、健常者を対象とした実験でも文字よりも数字の方が認識能力が高かったことから、そもそも数字の方が認識しやすいのではないかとも述べられている。その理由としては、アルファベットは一つの文字だけでは明確な意味を持たないが、数字は一つだけでも量という具体的な参照を持つゆえに、単なる視覚的記号として受動的に処理されるよりも、トップダウンの意味的な修飾を受けやすい可能性、あるいは数字認識は文字認識よりも右半球に側性化されているゆえに、左半球の損傷に起因する純粋失読の場合、比較的障害を免れやすい可能性などが指摘されている。
これらトリプルコード・モデルに関連したメタ分析は押し並べて成人を対象としたものだが、当然ながら子供を対象としたメタ分析、あるいは発達研究も参考になる。子供の数課題(数の大きさの比較やドットの数の推定など)と計算課題(足し算や引き算など)における神経相関の定量的メタ分析(14歳以下の定型発達児のfMRI研究のデータを使用)では、特に縁上回を中心とした下頭頂小葉からIPSの一部に及ぶ頭頂領域において、数課題は右半球優位、計算課題は左半球優位の活性化が認められており、それぞれの側性化が示されている。計算課題では上前頭回と内側前頭回から内側に伸びる背側前帯状回も主要な活性化領域であり、前帯状回は心的注意やワーキングメモリにとっても重要な、様々な高次認知活動の調整役と見なされることから、情動的動機から認知的目標への橋渡しを担っている可能性が示唆されている。また計算課題では中心前回から下前頭回および中前頭回へと広がる領域にも活性化が認められるが、中前頭回(背外側前頭前野)は手続きの複雑さやワーキングメモリ処理に関与しているものと考えられる。それら前頭-頭頂領域に加えて、計算課題では右側の島皮質と左側の前障の活性化も検出されており、この島皮質と前障は数課題でも小さな活性化が認められる。島皮質は外側溝の深部で側頭葉と前頭葉をつなぐ構造であり、前障はその島皮質と内側で隣接している。これらの領域については、島皮質は課題に対する内発的動機付け、前障はトップダウン処理とボトムアップ処理の統合に関与している可能性がある。成人の計算と比較した場合、子供の計算は前帯状回と島皮質が目立った活性化領域であり、これらは難しい問題解決にあたっての、自制心や内発動機付けと関連しているのかもしれない。
発達期における算術の神経相関のメタ分析では、前頭領域・頭頂領域・後頭-側頭領域・海馬を含む内側側頭領域からなる相互接続されたネットワークが浮かび上がり、計算において前頭-頭頂ネットワークが重要な役割を果たしていることなど、成人と重なる部分も多いが、特に成人との違いとして、(1)算術的事実学習の初期段階において、おそらく長期記憶の形成を反映して、海馬の活動増加が認められること、さらに海馬と前頭領域および頭頂領域との機能的結合性が強まること、(2)その海馬の活動が年齢を重ねるにつれて減少すると共に、事実検索への依存度の高まりを反映して、左の縁上回・角回前部・後頭-側頭領域の活動が増加すること、(3)暗記された事実検索への依存度が高まるにつれて、努力を要する手続き的な計算の負担が減り、ひいてはワーキングメモリや実行制御への依存度が下がり、それを反映して、背外側および腹外側前頭前野の活動が減少することなどが報告されている。
またそのような算術・計算の基盤として、当たり前と言えば当たり前にも聞こえるが、数的記号(数詞やアラビア数字)の習得こそが、基数性や序数性の理解などを通じて、非記号的な数的能力(主に物体の数を理解したり操作したりする能力)と正式な数学能力の橋渡しをする決定的な役割を果たすという知見がある。この点をまとめた総説によれば、(1)非記号的な数量処理は主に右頭頂葉に依存しており、その活動は発達を通じて安定している一方、(2)記号的な数処理は主に左頭頂葉に依存しており、その活動は発達を通じて増加するという、左右の非対称性があり、さらに(3)記号的な数処理の発達に伴って、非記号的な数量処理の精度も向上することが(単純な相関関係ではないが)示唆されている。これらの発達は多くの国々では、主として小学校からの算数教育によるだろう。
以上のような概観から、ピダハン族の場合、左頭頂葉に側性化された記号的数処理、前頭-頭頂ネットワークによる抽象的な数的表現や数的操作、海馬および左下頭頂小葉や上・中側頭回などに依存して記憶および想起される算術知識、右下側頭回後部または紡錘状回が初期処理を担う可能性のあるアラビア数字の認識、それらを含む複雑な計算処理ネットワークなどもまた発達しないことが推測される。とはいえ、伝統的には非常に限られた数詞しか用いないオーストラリア先住民の子供を対象とした実験では、対照群の英語を母語とするメルボルン在住の子供に比べて、視覚的な物体の数を記憶する際、先住民の被験者は言語に頼らず、空間的なパターン認識を多用して、それなりの正確性を示したという報告があり、ピダハン族の場合も記号的な数的能力が発達していない代わりに、別の能力が発達している可能性もあるかもしれない。またピダハン族の一部の村では既に、ブラジル政府がポルトガル語や数え方を学ぶ学校を設立しているので、数的能力を発達させたピダハン族も次第に増えていくものと思われる。
空間と数
その他の重要な知見としては、まず空間と数との関連性が挙げられる。前出のドゥアンヌらが提唱した数処理に関わる三つの頭頂回路のうち、pSPL(後上頭頂小葉)注意系回路は数処理に特異的ではなく、腕・手指・視線・注意の操作や制御、心的回転や空間性ワーキングメモリなどにも関与しており、そのような機能が心的数直線のような準空間的表現においても利用されている可能性が述べられていた。この心的数直線の存在は、数字の大小と空間的位置には関連があり、心的表現として左側に小さな数字、右側に大きな数字が配置されることを示唆する研究結果、すなわち小さな数字に対する反応は左手で速く、大きな数字に対する反応は右手で速いという傾向によって示唆されており、これはSNARC(Spatial-Numerical Association of Response Codes)効果と呼ばれる。一説にはIPS領域のうち、VIP野(腹側頭頂間溝野)には数量を表現する神経細胞群があり、LIP野(外側頭頂間溝野)は視線を中心とした座標空間を表現することから、このVIP-LIP回路が心的数直線とそれに沿った注意の移動を担っている可能性がある。
新生児においても左に小さな数量、右に大きな数量を相対的に関連付けるという研究があり、この結果は左から右へと方向付けられた数と空間の関連性、そこから類推できる心的数直線の存在が生得的であることを示唆しているとも解釈できる。だがその一方、(1)アラビア語など右から左へ読み書きする文化圏の場合、SNARC効果の向きが逆転すること、縦書きを習慣とする中国人の場合、中国語の数詞では上から下へのSNARC効果が生じること、読み書きの方向が相反する複数言語を身につけた人の場合、双方の影響が競合してSNARC効果が弱まること、イスラエル人の場合、言語は右から左へ読み書きするヘブライ語だが、アラビア数字は左から右へ読み書きする習慣を持っており、おそらく双方が相殺されてSNARC効果が見られないこと、パプアニューギニアのユプノ族やアマゾンのツィマネ族など、記号的経験に欠けた非工業化社会の人々は数と空間を関連付ける際、その方向に一貫性が認められないことなどから、SNARC効果は教育や文化の影響を受けることが示されており、(2)そのうえ一時的な課題の文脈(たとえば数字を定規上に思い浮かべるか時計盤上に思い浮かべるかなど)に応じても、その向きが非常に柔軟に変化したりもすることから、それは読み書き習慣によって不変に固定されているわけでもなく、(3)歴史的にも数直線の概念には普遍性が認められず、17世紀になってからようやく明確に出現したという知見があり、これらの証拠から、空間と数との関連付けは習慣やその時々の経験に応じて可変的であること、心的数直線のような内的表現はあくまで後天的な産物にすぎない可能性も示唆されている。
関連して示唆に富む知見としては、学校教育を受けていないユプノ族の場合、10までの数詞を理解しているにもかかわらず、それらの数を「端から端まで続く道」と説明された線分に対応付ける課題において、1(または2や3まで)は左の端に、それ以上の数はすべて右の端に振り分けるという行動を取り、連続した線分の範囲内にそれを配置することをしなかったというものがある。これは自発的に数直線の概念が投影されるかを調べる実験だったので、実験者は(過度の手がかりを与えないようにすべく)事前の実演として左端に1、右端に10を対応付けてみせるだけだったのだが、事前の実演の際、線分の中央に5も対応付けてみせた場合、被験者は左端に1と2という小さな数,中央に3~5という中くらいの数、右端に6~10という大きな数を振り分けた。ちなみに学校教育を受けたユプノ族の場合、線分上におおよそ均等に10までの数を配置してみせたので、数直線の概念を投影している可能性が高い。この結果は、不就学のユプノ族の場合、数を間隔尺度に従って線分に写像するのではなく、大小や大中小といった相対的なカテゴリーに分類したものと解釈できる。とはいえその後に実施されたまた別の、条件を変えた実験では、不就学のユプノ族も数量の大小に応じて線的な秩序を形成するという結果が出ており、課題の際、カテゴリー分けという解釈がなされた場合はそのように分類するが(ひとつ前の実験では、事前の実演によってこちらの解釈が誘発されたのだろう)、順序付けという解釈がなされた場合にはそのように並べてみせるという、文脈に応じた行動を取ることが示された。こうした知見を加味すれば、新生児は左に小さな数量、右に大きな数量を関連付ける偏向を生得的に持っているようだが、それが数直線のような水平方向の連続的表現に基づくかどうかは定かではなく、方向性を伴う相対的な分類や比較のようなものである可能性も考えられるかもしれない。
ある見解では興味深いことに、感情価(Valence)仮説を援用した動機付け仮説によって、左には小さな数量、右には大きな数量を位置付けるという、この非対称性の説明を試みている。感情価仮説とは、大脳半球の左右の前部領域がそれぞれ接近と回避の処理に特化しており、左(接近)は肯定的な感情、右(回避)は否定的な感情に関連しているという見方であり、それゆえに好ましい刺激は左半球を活性化させる一方、好ましくない刺激は右半球を活性化させる。加えて大脳には、左半球の活性化は右側への注意の方向付け、右半球の活性化は左側への注意の方向付けという対側性がある。そこから導かれる動機付け仮説では、乳児にとって、より多くの摂食につながる大きな数量はより好ましいものであり、それは肯定的な動機付けとして左半球を活性化させるので、結果として右側へ注意が向けられるという見方が提案されている。これが右側に大きな数量が関連付けられる素因であり、対照的に左側には小さな数量が関連付けられるものと仮定される。
空間-数の関連性(Spatial-Numerical Association; SNA)それ自体については、上記のとおり文化的影響を受けるにしても、乳幼児や動物の諸研究の蓄積から、生得的なものであることが強く示唆されている。この関連性がどのような仕組みに基づいているかについては、空間と数、さらには時間やその他の量的次元がすべて共通の一般化大きさシステム(Generalized Magnitude System; GMS)によって処理されているという、大きさ理論(A Theory Of Magnitude; ATOM)が過去に提唱されたりもしたが、様々な研究を多角的にまとめた総説によれば、少なくとも幼児期以降にはそれらの量的表現はそれなりに分離している証拠が数多くあり、近年では、仮に生まれつきには共通の処理システムが存在するという立場を取るにしても、それは乳児期以降の発達に伴って分岐していくという見方が提示されている。そして幼児期の後、教育段階における数学的思考と空間的思考との関連性については、視空間的なイメージを生成・想起・維持・操作する能力、すなわち空間的視覚化こそが、とりわけ新しい解法を生み出すにあたって重要な役割を果たすという見解がある。ある研究では、心的イメージ能力を生成・維持・変換・走査という四つの下位構成要素に分類した場合(イメージ走査とは、心的イメージにおいて注意を移動させる能力)、心的回転課題によって計られたイメージ変換能力のみが、小学生の計算能力と相関しており、従ってイメージの視覚的表現(初期視覚野が関与)よりも空間的変換(頭頂皮質が関与)こそが、数学的技能と密接な関連性があること、ひいては数学的思考に寄与する空間的視覚化とは、(おそらく心的回転だけには限られないが)視空間的なイメージ変換能力であることが示唆された。
同様に空間的視覚化に着目して、心的回転と数的・数学的推論の神経相関、それぞれの重複と乖離を探索した定量的メタ分析(総計83のfMRI研究論文が対象)によれば、(1)心的回転は両側の頭頂葉(特に右IPS・右楔前部)および前頭葉、(2)記号的数処理は両側の頭頂葉および右前頭葉、(3)暗算は左IPSおよび多くの両側の頭頂・前頭諸領域の活動とそれぞれ関連しており、これら三つの認知課題すべてにおいて、IPSおよび上下頭頂小葉に最大の収束領域があり、またいずれも前頭領域の活動も認められた。さらに連結分析および対照分析の結果、(1)心的回転では右IPSが最大の活性化領域である一方、記号的数処理と暗算では左IPSが最大の活性化領域であり、(2)心的回転では右側の楔前部・上頭頂小葉に際立った活性化があり、(3)心的回転と暗算に共通する最大の活性化領域は右楔前部、なおかつ双方ともに前頭領域では中前頭回の活動と関連しており、(4)暗算と記号的数処理はともに左IPSを含む両側の下頭頂小葉に際立った活性化があり、(5)暗算と記号的数処理はともに右島皮質および前障の活動とも関連しているという概観が示された。これらのうち、数的推論全般に前頭-頭頂ネットワークが関与していること、記号的数処理や暗記された計算結果の想起には左IPSや左角回を含む左下頭頂小葉が関与していることなどは、既出の諸研究でも示された多くの知見と一致している。さらに加えて、(1)心的回転と暗算に共通する(特に左側の)中前頭回が一般的な心的操作に関与している可能性があること、(2)同じく心的回転と暗算に共通する活性化領域であり、なおかつ心的回転に強く関連する領域でもある楔前部は、視覚-空間イメージ・空間における注意の方向付け・目標指向性の運動の計画や想像などに関与しているという知見があり、そのような機能が数学的推論に利用されていることも示唆された。そしてそのように空間的思考が数学的思考に利用されるメカニズムとしては、長い歴史を経て進化的に適応した脳の空間的・感覚運動的能力、つまり元々は道具・物体・空間内の場所と相互作用するために生じた機能が、人類史において新しい文化的発明である数学に共同利用または転用されて、神経基盤を共有するようになったという見方が提起されている。これはドゥアンヌとコーエンが提唱した神経細胞リサイクル仮説に基づいており、この仮説によれば、読字や数学のような文化的技能は、学習主導型の脳の可塑性を通じて、それらの技能と進化的に類似した機能を有する既存の神経回路に侵入することで、特定の皮質領域を再編成する。ただしその学習主導型の可塑性は何でも柔軟に取り入れることができる広範なものではなく、進化および脳の組織化によって強固に制約されており、文化的習得に浸食されても、元々の機能や構成が完全に上書きされることはない。
心的回転に代表されるような、視空間的な心的イメージ操作が数的・数学的推論と深く関連しているという上記のような知見は、ピダハン族が心的回転の必要な課題を苦手としたこと、アカルキュリアを構成要素とするゲルストマン症候群の根底には心的イメージ障害があるという仮説などと整合性がある。とはいえ上段のメタ分析では、ともに左右両側が関与しているにせよ、心的回転の活性化領域も、それと暗算と共通する活性化領域も、どちらかと言えば右頭頂葉であることが示されており、ゲルストマン症候群は通常、左頭頂葉損傷に起因するので一見、左右が食い違っているようにも思える。だが実のところ、右頭頂葉損傷は空間性のアカルキュリアを引き起こすことが以前から報告されている。たとえば24人の右半球損傷患者の数的能力を検査した研究では、特に左半側空間無視(空間や物体の左側に注意が向かない障害)を有する患者は様々な課題の成績が悪く、なかでも一桁の掛け算の暗算に障害が見られたが(空間無視がない患者も多少の誤りは犯したが、軽微な割合に留まった)、興味深いことに、それらの患者の空間無視は心的イメージにまで及んでおり、内的表現に注意を向けることに困難が生じている可能性が指摘された。一桁の掛け算は主として左角回(またはその隣の左縁上回)を介した言語性算術的事実の自動検索に依存するというのが定説だが、単に九九を暗唱するなどではなく問題として解く場合、右頭頂葉の担う心的な数量表現、それもおそらくは(それこそ心的数直線と解釈されるような)空間的な数量表現がそれを下支えしているのかもしれない。
実際、アメリカの高校生を対象としたfMRI研究では、一桁の計算の正誤を判定する課題において、右IPSの活性化が大きい学生ほど、相関してPSAT(大学受験の予備テスト)の数学の成績が悪く、左縁上回の活性化が大きい学生ほど、その成績が良かったという研究もあり、これは一桁の計算でも心的な数量表現への依存があること、そのような心的な数量表現に頼らず、言語性の事実検索が自動化されている人ほど計算能力が高いことを示唆する。他にも多桁の掛け算の暗算における神経相関を調べた研究では、小学校戦略(小さな桁から掛けていく)と熟練者戦略(最も大きな桁から掛けていく)を比較したところ、小学校戦略の方が内的な空間的表現と注意に関与するpSPL(後上頭頂小葉)の活性化が大きく、その活性化は右優位かつ楔前部にも及び、特に桁数が多い問題の場合、心的表現の保持と変換に関与するPPC(後頭頂皮質)の活性化も強まった。これは自動的な記憶検索だけでは済まず、複雑な段階を要する問題を解く際、熟練していない計算手続きを取るほどに、空間的視覚化に依存する傾向があることを示唆している。
また別の空間性アカルキュリアの症例では、右側の角回・縁上回・シルヴィウス溝(外側溝)周辺領域を損傷したPNという患者の場合、暗記された算術的事実の想起は無事であり、算術手続きそれ自体の論理的知識も保存されていたにもかかわらず、多桁の掛け算を筆算で解く際、繰り上がる数をどこに書いてどこに加えるかを間違えたり、部分積を適切な位置に書けなかったり、数の列を混同したりといった空間的な誤りを多く犯したことが報告されている。多桁の足し算や引き算には問題がなかったことから、これは複雑な空間的図式の知識が必要な筆算において、数の空間的な配置手続きに障害が生じているものと解釈された(割り算も同様の可能性があるが、割り算の筆算は学業から離れると手順を忘れてしまう人も多いゆえに課題から外された)。
多桁の暗算にせよ筆算にせよ、通常はそれを構成要素に分解して計算したのち、足し合わせたりして答えを出すものであり、分解された単純な計算がたとえ左頭頂葉の暗記された事実検索に多くを依存しているにしても、結局のところ、それにも右頭頂葉は関与しているようだ。この左右の役割に関しては、次のような知見も参考になる。脳腫瘍患者9人を被験者として、その開頭手術中、直接皮質電気刺激(Direct Cortical Electrostimulation; DCE)により、主に左右の頭頂葉の上頭頂小葉・IPS水平部・IPS腹側部・角回・縁上回を刺激しながら、一桁の単純な計算をしてもらった研究では(局所麻酔で頭蓋骨の一部を開くだけなので意識はあり、脳そのものは痛みを感じないので直接電極を貼って刺激できる)、左頭頂葉を刺激して不活性化させた場合、解答に近似的な誤り(たとえば8×3=25)が生じる傾向が非常に強く、これは右頭頂葉の厳密性を欠いた概算で対処した可能性を示唆するが、その一方、右頭頂葉を刺激して不活性化させた場合、解答に検索の誤り(たとえば8×3=32)が生じる傾向が増え、これは左頭頂葉が暗記された掛け算表から知識を取り出す際、近接する項目が干渉した可能性(この例の場合は8×4の答えが誤って呼び出された可能性)を示唆する。同様の傾向は一桁の足し算でも認められた。この結果は一桁の単純な計算であっても、近似による概算を担う右頭頂葉と記号的計算の検索を担う左頭頂葉がともに協調して、相互に補完し合いながら、解の導出に寄与していることを示唆している。つまり暗記された知識を想起する場合でも、おおよその数値を絞り込んだり結果の妥当性を評価したりするような右頭頂葉による近似表現がやはり、左頭頂葉による検索を下支えしているのだろう。ちなみに掛け算の場合、左頭頂葉では角回よりもむしろ縁上回の不活性化で近似的な誤りが生じる傾向があり、右頭頂葉の不活性化による検索の誤りでは、角回・縁上回・IPS・上頭頂小葉など、それを生じさせる部位がばらついていた。加えて左右の皮質下への刺激でも掛け算と足し算の誤りが生じた。これらは単純な計算であっても、それに関わる数処理が頭頂内および頭頂間、そして皮質下など他領域へも、ネットワークとして広がっていることを支持している。この実験を行った著者らは、数学機能の側性化についての総説において、かつては分離脳研究に基づき、ほぼ左半球だけが数学を担っているとされていたが、現在では左右半球の複雑な編成によってそれが担われているという豊富な証拠があることを提示した。その中でひとつ興味深いのは、右島皮質を損傷すると複雑な数字列におけるゼロの誤配置が生じる(読み書きにおいて40265を4265としたり、107を1007としたりする)という知見であり、上述の空間性アカルキュリア患者PNも多桁の掛け算を筆算で解く際、不要な0を生成してしまうという行動を見せた。なぜそうなるのかについては、さほど説得力の感じられる説明はないようだが。
いずれにしても、ゲルストマン四徴のうちのアカルキュリアについては、左右いずれの頭頂葉損傷によっても生じうることが分かる。発達において初期の非記号的な数量処理は右頭頂葉優位であり、のちに左頭頂葉優位の記号的な数処理が発達していっても、それを右頭頂葉が下支えしているということは、初歩的な数的能力にはむしろ右半球の方が重要ということを示唆しているのかもしれない。数学学習困難(ディスカルキュリアを含むより広範な数学的技能の学習障害)のメタ分析においても、とりわけ右IPSおよび右前頭-頭頂ネットワークの異常が報告されており、そのことから、右IPSは記号的な数処理にも関与していることが強調されている。
そして次に、指と数との関連性を重視する見方もある。手指失認のくだりで以前にも触れたように、生まれつき手足がない人でも数学は身につけられるので、指数えが計数や足し引きの習得に必須というわけではなく、実際にそれを支持する証拠もあるが(ただし先天性四肢欠損症の子供が幻肢の手指で数を数え、簡単な算数の問題を解いていたという報告もある)、経験に基づく関連性にせよ、指と数や計算との神経相関を示すfMRI研究は少なくない。たとえば、指数えの習慣が異なる二群(左手から指数えを開始する群と右手から指数えを開始する群)に一桁の数字や数詞を提示すると、明らかには指を動かしていないにもかかわらず、小さな数の場合、数え始める手とは逆の大脳半球(手の制御は対側性なので、要するに数え始める手に対応する方)の運動前野が活性化した。このような知見に関連して、SNARC効果の向きは読み書きの習慣よりも、むしろ指数えの習慣による文化的影響を受けるという説もある。
あるいは18人の成人を対象として、算術課題(引き算および掛け算)と指弁別課題(画面に表示された手の特定の指を識別して、自分の手は見ないまま、体性感覚をたよりに自分の同じ指を対応させる課題)における神経相関を比較した研究では、特に左側のhIPS(頭頂間溝水平部)、および両側のpSPL(IPSの後部から楔前部へ広がる後上頭頂小葉領域)において、算術と指弁別に共通した活性化があり、その活性化パターンに正の相関も認められた。算術課題では検索に多くを依存する掛け算よりも、特に引き算において指弁別との共通活性化が認められており、学習初期の児童は引き算の際によく指を使うことから、この結果はhIPSおよびpSPLが順序付けられた系列および段階的変化の追跡(心的表現に対する注意の移動)を担っており、それが数と指に共通する離散的表現を媒介することを示唆している。ちなみに指弁別に特異的な活性化領域は、両側の外側後頭側頭皮質の一部である有線外皮質身体領域(Extrastriate Body Area; EBA)、識別した手指とは対側の頭頂葉最前部に位置するS1 (一次体性感覚野)、同じく対側の前頭葉最後部に位置するM1 (一次運動野)であり、EBA・S1・M1はそれぞれ身体部位に対応した視覚的・体性感覚的・運動的表現に関与するものとされる。それらがhIPS/pSPLと共に、EBA–PSPL/hIPS–S1/M1という一連の神経ネットワークをなしているようだ。そのうちのEBAは顔以外の身体部位の認識、行為の符号化などに関与していると考えられており、EBAを含む外側後頭側頭皮質(Lateral Occipitotemporal Cortex; LOTC)には、顔や人体や物体や動物や情景などのほか、手に選択的に反応する領域、それと密接に重なる道具に反応する領域などもある。
指数えの方向(たとえば左手から右手へ)や指の順序付けられた系列などは、いずれも空間的性質を持っており、それが心的表現を構成するとすれば、指と数との関連性も結局のところ、空間と数との関連性に包含されるだろう。そしてそれが内的な空間的表現に基づくとすれば、やはり心的イメージとの関連性も推測される。これについては、前述のH.P.という純粋なゲルストマン症候群患者の症例が参考になるかもしれない。H.P.は一般的な知的能力の障害や失語症などは認められなかったにもかかわらず、数や計算に関わる処理全般に障害がある純粋な包括的アカルキュリアを呈していた。
①口頭での数唱では指を使って数えなければならず、数えるのが非常に遅く、途中の数を飛ばしてしまうこともあり、3つずつ数えたり、逆方向に数えたりすることはできなかった。アラビア数字や数詞の書字でも同様だった。その一方、他人の数唱を復唱することは可能だった。
②ランダムに配置された(つまりパターン認識ができない)ドットが特に5つ以上ある場合、その数え上げに誤りを犯した。
③数詞の読み書きは良好だったが、アラビア数字の読み書きに重度の障害があり、アラビア数字から数詞へ、あるいはその逆の変換にも大きな障害があった。特にアラビア数字を数詞に変換する場合、三桁以上の数になると統語的な誤りを多く犯した。たとえば2612というアラビア数字列は、数詞では「二千六百十二」と読むべきだが、それを「二十六千十二」と読んでしまったりした。統語的に誤った数詞の読み方の判断を求められた際、たとえば「六十五百二十四」などを正しいものとして受け入れてしまった。これらは数詞表記の統語規則の喪失を示唆している。
④数の大きさの比較にも障害があり、正確な数値による判断ではなく、視覚的または語彙的な手がかりに依存して推定していた。具体的には、最も大きな桁数で比較するという戦略を採っており、アラビア数字の場合、「329」と「325」のような大きな桁が同じものに限って誤答していた。また数詞の場合、英語で言えば「a hundred-thousand and sixty-five」と「three-hundred thousand」との比較において、後者(300,000)の方が大きな数にもかかわらず、最初の言葉である「a hundred」と「three」だけを比較して、前者(100,065)の方が大きいと誤判断したりした(スイスの患者なので実際にはフランス語が用いられている)。
⑤計算では暗記された知識の検索に障害があり、暗算ができなかった。自由なやり方を許されると、足し算でさえ自分でドットを書き、そのドットを指で数えることで回答した。引き算の手順にも問題があり、十の位が1までは良好な成績だったが、十の位が2を超えると成績が落ち、たとえば67引く1を56と答えるなどした。掛け算表は2の段ですら想起できず、割り算はまったくできなかった。選択肢から最も近似的な数を選択する問題でも誤りを犯して、概算にも困難を示した。
⑥筆算においては、数の桁数を正しく揃えて視覚的に配置する課題には問題はなかった。だが計算それ自体には障害があり、繰り上がりの誤り、掛け算の手順の喪失、引き算では繰り下がりが分からないのか、上下段の位置関係を無視して常に大きな数から小さな数を引くという誤りを犯した。
⑦視覚的または聴覚的に提示された数を垂直のスケール(0・50・100の三つの目盛りが与えられる)の上に配置する課題では、ためらいながらも、どうにか目盛りと比較して妥当な回答をした。だが、始点と終点だけの目盛りのない直線上に数を位置付けることはできず、指示された数の意味が分からないと言った。
⑧1分間に100以下の数をできるだけ多く口頭で言うように求められても、9個しか口に出せなかった。それも順序立てて数えたりはせず、完全に無作為な数ばかりだった。
⑨繰り返しの質問を通じて、実験者が頭の中で選んだ100以下の数を当てるという課題において、メモを許されたにもかかわらず、正解に辿り着くのに約90分もかかった。「20と30の間ですか?」と質問した直後に「40と80の間ですか?」と質問するなどして、正解の範囲を狭めるために必要な数の意味的表現が損なわれているようだった。
⑩写真を見て対象の高さ・重さ・個数などの数量を推定することに重度の障害があり、傘の重さを10キロと答えたりした。だが自分の体重など既知の基準と比較できた場合、その対象の数量(写真に写った人物の体重)を妥当に答えることができた。20枚は手紙の分量として多すぎるか少なすぎるか、一週間の日数といった文脈的または事実的な知識に基づく問題であれば正しく答えることができた。それはにはおそらく数量の推定が必要ではなく、実際、自分自身や日常生活に関する自伝的・百科事典的な数量の知識(自分の身長や牛乳の値段など)に関しては障害が見られなかった。
⑪形式的推論課題において、「非動物で構成されていない群とは?」といった意味的・統語的に入り組んだ理解が必要な論理関係の記述問題では、正常範囲内の成績を収めることができたが、「ポールはヘンリーより背が高いが、ルイよりも背が低い。誰が一番背が高い?」といった大きさ関係の記述問題の場合、非常に成績が悪かった。しかし後者の場合も、問題を視覚的な図式として提示した場合(下掲の例図参照)、正常な成績になった。
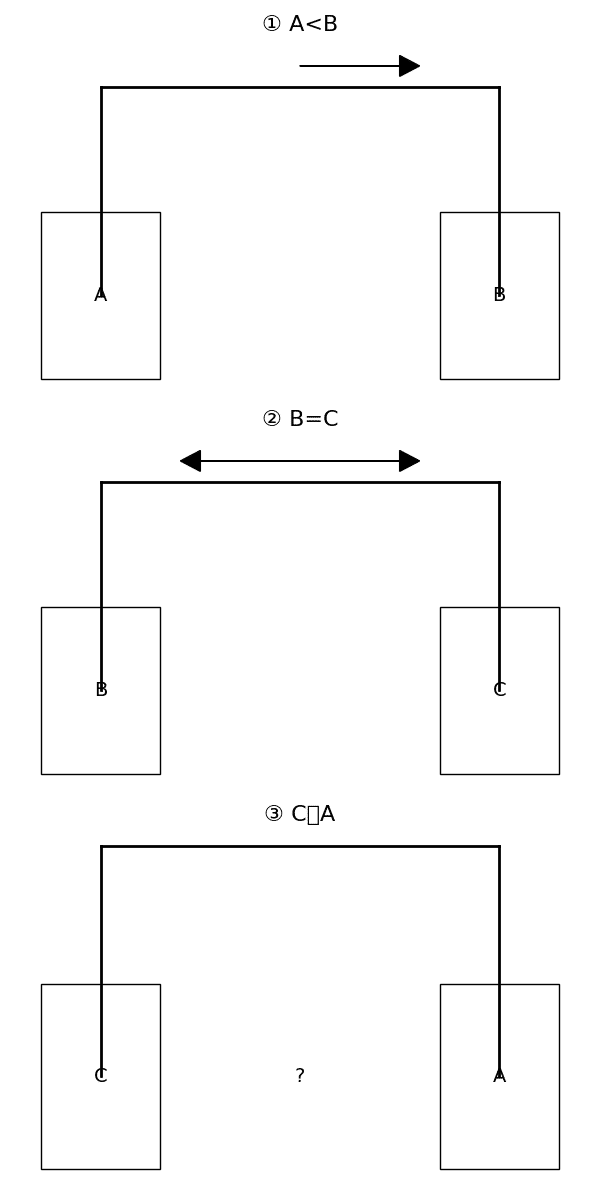
以上から、Subitizing範囲を超える非記号的な数表現(②)、非記号的な大きさの比較(⑪)、概数的な数量の比較や推定(⑨⑩)、基本的な数の序列(①⑧)、アラビア数字の処理(③)、記号的な数の比較(④)、暗記された算術的事実検索(⑤)、筆算(⑥)、繰り上がりや繰り下がりなどの計算手順(⑤⑥)、数直線的な意味表現(⑦)など、これまでに見てきた数的・数学的能力に包括的な障害が認められる。そしてH.P.の病変は左角回の深部皮質下に限局しており、下頭頂小葉は無事のまま、より深い皮質下構造の視床や基底核にも及ばずに、角回前部を後頭-側頭領域や上頭頂小葉から孤立させていた。またH.P.のゲルストマン症候群に関する論文では、右側の同じ領域に接続する連合線維も遮断されていることが示唆されていた。つまりおそらく、数量表現に関与する右頭頂葉、記号的数表現に関与する左頭頂葉、筆算の空間的手続きの想起に関与する右角回、言語性算術的事実の想起に関与する左角回や左縁上回や左側頭葉、内的な注意操作に関与する後上頭頂小葉など、数的処理や算術処理の際に連携して機能するはずの諸領域間の、ネットワーク接続が遮断されてしまっているのだろう。視空間的な心的イメージに特に関与する後頭頂葉内側の楔前部もおそらく、その断絶に含まれるものと思われる。実際、H.P.は課題において、量的・順序的な心的表現を思い浮かべる必要がある場合、非常な困難を示した一方、視覚的に手がかりを提示されれば、それをたよりに答えることができた。たとえば足し算の暗算さえできなかったが、それを視覚的にドットとして書いて解いた。始点と終点だけの直線には数を位置付けられなかったが、目盛りがあればおおよその位置付けができた。三者の身長の高さ関係を問われる課題でも、文章問題では成績が悪かったが、図式問題にすると正答できた。これらは心的イメージの障害を強く示唆しており、H.P.はゲルストマン症候群の他の要素に関しても、とりわけ自分の手が見えない条件において手指失認、心的回転が必要な条件において左右識別障害を示した。
H.P.は「文字に関しては一貫性があるが、数に関してはそれを何にも結びつけることができない。それが何であるか分からない」と述べており、このアカルキュアに焦点を絞った論文の著者らは、ドゥアンヌらの提唱した心的数直線、SNARC効果なども引き合いに出しながら、H.P.は数の連続的・順次的な表現を喪失している可能性があること、ひいてはイメージの心的表現に影響する障害、空間的な心的イメージ操作の障害がこの困難を説明できる可能性があることを示唆している。
文献
*129 Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in cognitive sciences, 8(7), 307–314. https://doi.org/10.1016/j.tics.2004.05.002
*130 Nieder A. (2021). Neuroethology of number sense across the animal kingdom. The Journal of experimental biology, 224(Pt 6), jeb218289. https://doi.org/10.1242/jeb.218289
*131 Agrillo, C., Piffer, L., Bisazza, A., & Butterworth, B. (2012). Evidence for two numerical systems that are similar in humans and guppies. PloS one, 7(2), e31923. https://doi.org/10.1371/journal.pone.0031923
*132 Revkin, S. K., Piazza, M., Izard, V., Cohen, L., & Dehaene, S. (2008). Does subitizing reflect numerical estimation?. Psychological science, 19(6), 607–614. https://doi.org/10.1111/j.1467-9280.2008.02130.x
*133 Hyde, D. C., & Spelke, E. S. (2009). All numbers are not equal: an electrophysiological investigation of small and large number representations. Journal of cognitive neuroscience, 21(6), 1039–1053. https://doi.org/10.1162/jocn.2009.21090
*134 Hyde, D. C., & Spelke, E. S. (2011). Neural signatures of number processing in human infants: evidence for two core systems underlying numerical cognition. Developmental science, 14(2), 360–371. https://doi.org/10.1111/j.1467-7687.2010.00987.x
*135 Piazza, M., Fumarola, A., Chinello, A., & Melcher, D. (2011). Subitizing reflects visuo-spatial object individuation capacity. Cognition, 121(1), 147–153. https://doi.org/10.1016/j.cognition.2011.05.007
*136 Ester, E. F., Drew, T., Klee, D., Vogel, E. K., & Awh, E. (2012). Neural measures reveal a fixed item limit in subitizing. Journal of Neuroscience, 32(21), 7169–7177. https://doi.org/10.1523/JNEUROSCI.1218-12.2012
*137 Choo, H., & Franconeri, S. L. (2014). Enumeration of small collections violates Weber’s law. Psychonomic bulletin & review, 21, 93–99. https://doi.org/10.3758/s13423-013-0474-4
*138 Cutini, S., Scatturin, P., Moro, S. B., & Zorzi, M. (2014). Are the neural correlates of subitizing and estimation dissociable? An fNIRS investigation. Neuroimage, 85, 391–399. https://doi.org/10.1016/j.neuroimage.2013.08.027
*139 Hyde, D. C. (2011). Two systems of non-symbolic numerical cognition. Frontiers in human neuroscience, 5, 150. https://doi.org/10.3389/fnhum.2011.00150
*140 Cheyette, S. J., & Piantadosi, S. T. (2020). A unified account of numerosity perception. Nature human behaviour, 4(12), 1265–1272. https://doi.org/10.1038/s41562-020-00946-0
*141 Vuokko, E., Niemivirta, M., & Helenius, P. (2013). Cortical activation patterns during subitizing and counting. Brain research, 1497, 40–52. https://doi.org/10.1016/j.brainres.2012.12.019
*142 Vetter, P., Butterworth, B., & Bahrami, B. (2011). A candidate for the attentional bottleneck: set-size specific modulation of the right TPJ during attentive enumeration. Journal of Cognitive Neuroscience, 23(3), 728–736. https://doi.org/10.1162/jocn.2010.21472
*143 Xu, Y., & Chun, M. M. (2009). Selecting and perceiving multiple visual objects. Trends in cognitive sciences, 13(4), 167–174. https://doi.org/10.1016%2Fj.tics.2009.01.008
*144 Knops, A., Piazza, M., Sengupta, R., Eger, E., & Melcher, D. (2014). A shared, flexible neural map architecture reflects capacity limits in both visual short-term memory and enumeration. The Journal of neuroscience : the official journal of the Society for Neuroscience, 34(30), 9857–9866. https://doi.org/10.1523/JNEUROSCI.2758-13.2014
*145 Ansari D. (2008). Effects of development and enculturation on number representation in the brain. Nature reviews. Neuroscience, 9(4), 278–291. https://doi.org/10.1038/nrn2334
*146 Nieder, A., & Dehaene, S. (2009). Representation of number in the brain. Annual review of neuroscience, 32, 185–208. https://doi.org/10.1146/annurev.neuro.051508.135550
*147 Harvey, B. M., Fracasso, A., Petridou, N., & Dumoulin, S. O. (2015). Topographic representations of object size and relationships with numerosity reveal generalized quantity processing in human parietal cortex. Proceedings of the National Academy of Sciences of the United States of America, 112(44), 13525–13530. https://doi.org/10.1073/pnas.1515414112
*148 Lorenzi, E., Perrino, M., & Vallortigara, G. (2021). Numerosities and other magnitudes in the brains: a comparative view. Frontiers in Psychology, 12, 641994. https://doi.org/10.3389/fpsyg.2021.641994
*149 Cai, Y., Hofstetter, S., van Dijk, J., Zuiderbaan, W., van der Zwaag, W., Harvey, B. M., & Dumoulin, S. O. (2021). Topographic numerosity maps cover subitizing and estimation ranges. Nature communications, 12(1), 3374. https://doi.org/10.1038/s41467-021-23785-7
*150 Tsouli, A., Harvey, B. M., Hofstetter, S., Cai, Y., van der Smagt, M. J., Te Pas, S. F., & Dumoulin, S. O. (2022). The role of neural tuning in quantity perception. Trends in Cognitive Sciences, 26(1), 11–24. https://doi.org/10.1016/j.tics.2021.10.004
*151 Roggeman, C., Santens, S., Fias, W., & Verguts, T. (2011). Stages of nonsymbolic number processing in occipitoparietal cortex disentangled by fMRI adaptation. The Journal of neuroscience : the official journal of the Society for Neuroscience, 31(19), 7168–7173. https://doi.org/10.1523/JNEUROSCI.4503-10.2011
*152 Halpern, C., Clark, R., Moore, P., Cross, K., & Grossman, M. (2007). Too much to count on: impaired very small numbers in corticobasal degeneration. Brain and cognition, 64(2), 144–149. https://doi.org/10.1016/j.bandc.2007.01.006
*153 Koss, S., Clark, R., Vesely, L., Weinstein, J., Powers, C., Richmond, L., Farag, C., Gross, R., Liang, T. W., & Grossman, M. (2010). Numerosity impairment in corticobasal syndrome. Neuropsychology, 24(4), 476–492. https://doi.org/10.1037/a0018755
*154 Morgan, B., Gross, R. G., Clark, R., Dreyfuss, M., Boller, A., Camp, E., Liang, T. W., Avants, B., McMillan, C. T., & Grossman, M. (2011). Some is not enough: quantifier comprehension in corticobasal syndrome and behavioral variant frontotemporal dementia. Neuropsychologia, 49(13), 3532–3541. https://doi.org/10.1016/j.neuropsychologia.2011.09.005
*155 Hyde, D. C., Boas, D. A., Blair, C., & Carey, S. (2010). Near-infrared spectroscopy shows right parietal specialization for number in pre-verbal infants. NeuroImage, 53(2), 647–652. https://doi.org/10.1016/j.neuroimage.2010.06.030
*156 Kersey, A. J., & Cantlon, J. F. (2017). Neural Tuning to Numerosity Relates to Perceptual Tuning in 3-6-Year-Old Children. The Journal of neuroscience : the official journal of the Society for Neuroscience, 37(3), 512–522. https://doi.org/10.1523/JNEUROSCI.0065-16.2016
*157 Vogel, S. E., Goffin, C., & Ansari, D. (2015). Developmental specialization of the left parietal cortex for the semantic representation of Arabic numerals: an fMR-adaptation study. Developmental cognitive neuroscience, 12, 61–73. https://doi.org/10.1016/j.dcn.2014.12.001
*158 Piazza, M., Mechelli, A., Price, C. J., & Butterworth, B. (2006). Exact and approximate judgements of visual and auditory numerosity: an fMRI study. Brain research, 1106(1), 177–188. https://doi.org/10.1016/j.brainres.2006.05.104
*159 Sokolowski, H. M., Hawes, Z., Peters, L., & Ansari, D. (2021). Symbols are special: an fMRI adaptation study of symbolic, nonsymbolic, and non-numerical magnitude processing in the human brain. Cerebral Cortex Communications, 2(3), tgab048. https://doi.org/10.1093/texcom/tgab048
*160 Demeyere, N., Rotshtein, P., & Humphreys, G. W. (2012). The neuroanatomy of visual enumeration: Differentiating necessary neural correlates for subitizing versus counting in a neuropsychological voxel-based morphometry study. Journal of Cognitive Neuroscience, 24(4), 948–964. https://doi.org/10.1162/jocn_a_00188
*161 Himmelbach, M., Erb, M., Klockgether, T., Moskau, S., & Karnath, H. O. (2009). fMRI of global visual perception in simultanagnosia. Neuropsychologia, 47(4), 1173–1177. https://doi.org/10.1016/j.neuropsychologia.2008.10.025
*162 Dehaene, S., & Cohen, L. (1994). Dissociable mechanisms of subitizing and counting: neuropsychological evidence from simultanagnosic patients. Journal of Experimental Psychology: Human perception and performance, 20(5), 958. https://psycnet.apa.org/doi/10.1037/0096-1523.20.5.958
*163 Dalrymple, K. A., Barton, J. J., & Kingstone, A. (2013). A world unglued: simultanagnosia as a spatial restriction of attention. Frontiers in human neuroscience, 7, 145. https://doi.org/10.3389/fnhum.2013.00145
*164 Mazza V. (2017). Simultanagnosia and object individuation. Cognitive neuropsychology, 34(7-8), 430–439. https://doi.org/10.1080/02643294.2017.1331212
*165 Lemer, C., Dehaene, S., Spelke, E., & Cohen, L. (2003). Approximate quantities and exact number words: Dissociable systems. Neuropsychologia, 41(14), 1942–1958. https://doi.org/10.1016/S0028-3932(03)00123-4
*166 Ashkenazi, S., Henik, A., Ifergane, G., & Shelef, I. (2008). Basic numerical processing in left intraparietal sulcus (IPS) acalculia. Cortex, 44(4), 439–448. https://doi.org/10.1016/j.cortex.2007.08.008
*167 Demeyere, N., Lestou, V., & Humphreys, G. W. (2010). Neuropsychological evidence for a dissociation in counting and subitizing. Neurocase, 16(3), 219–237. https://doi.org/10.1080/13554790903405719
*168 Green, C. S., & Bavelier, D. (2006). Enumeration versus multiple object tracking: the case of action video game players. Cognition, 101(1), 217–245. https://doi.org/10.1016/j.cognition.2005.10.004
*169 Scolari, M., Vogel, E. K., & Awh, E. (2008). Perceptual expertise enhances the resolution but not the number of representations in working memory. Psychonomic bulletin & review, 15(1), 215–222. https://doi.org/10.3758/pbr.15.1.215
*170 Le Corre, M., & Carey, S. (2007). One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles. Cognition, 105(2), 395–438. https://doi.org/10.1016/j.cognition.2006.10.005
*171 Hurford, J. R. (1987). Language and number: The emergence of a cognitive system. New York: B. Blackwell.
*172 Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical cognition, 1(1), 83–120. https://www.unicog.org/publications/DehaeneCohen_TripleCodeModelNumberProcessing_MathCognition1995.pdf
*173 Zorzi, M., Priftis, K., & Umiltà, C. (2002). Neglect disrupts the mental number line. Nature, 417(6885), 138–139. https://doi.org/10.1038/417138a
*174 Arsalidou, M., & Taylor, M. J. (2011). Is 2+ 2= 4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage, 54(3), 2382–2393. https://doi.org/10.1016/j.neuroimage.2010.10.009
*175 Rosenberg-Lee, M., Chang, T. T., Young, C. B., Wu, S., & Menon, V. (2011). Functional dissociations between four basic arithmetic operations in the human posterior parietal cortex: a cytoarchitectonic mapping study. Neuropsychologia, 49(9), 2592–2608. https://doi.org/10.1016/j.neuropsychologia.2011.04.035
*176 Klein, E., Suchan, J., Moeller, K., Karnath, H. O., Knops, A., Wood, G., Nuerk, H. C., & Willmes, K. (2016). Considering structural connectivity in the triple code model of numerical cognition: differential connectivity for magnitude processing and arithmetic facts. Brain structure & function, 221(2), 979–995. https://doi.org/10.1007/s00429-014-0951-1
*177 Moeller, K., Willmes, K., & Klein, E. (2015). A review on functional and structural brain connectivity in numerical cognition. Frontiers in human neuroscience, 9, 227. https://doi.org/10.3389/fnhum.2015.00227
*178 Sokolowski, H. M., Fias, W., Mousa, A., & Ansari, D. (2017). Common and distinct brain regions in both parietal and frontal cortex support symbolic and nonsymbolic number processing in humans: A functional neuroimaging meta-analysis. Neuroimage, 146, 376–394. https://doi.org/10.1016/j.neuroimage.2016.10.028
*179 Sokolowski, H. M., Matejko, A. A., & Ansari, D. (2023). The role of the angular gyrus in arithmetic processing: a literature review. Brain structure & function, 228(1), 293–304. https://doi.org/10.1007/s00429-022-02594-8
*180 Zamarian, L., Ischebeck, A., & Delazer, M. (2009). Neuroscience of learning arithmetic—Evidence from brain imaging studies. Neuroscience & Biobehavioral Reviews, 33(6), 909–925. https://doi.org/10.1016/j.neubiorev.2009.03.005
*181 Fresnoza, S., Christova, M., Purgstaller, S., Jehna, M., Zaar, K., Hoffermann, M., Mahdy Ali, K., Körner, C., Gallasch, E., von Campe, G., & Ischebeck, A. (2020). Dissociating Arithmetic Operations in the Parietal Cortex Using 1 Hz Repetitive Transcranial Magnetic Stimulation: The Importance of Strategy Use. Frontiers in human neuroscience, 14, 271. https://doi.org/10.3389/fnhum.2020.00271
*182 Grabner, R. H., Ischebeck, A., Reishofer, G., Koschutnig, K., Delazer, M., Ebner, F., & Neuper, C. (2009). Fact learning in complex arithmetic and figural-spatial tasks: the role of the angular gyrus and its relation to mathematical competence. Human brain mapping, 30(9), 2936–2952. https://doi.org/10.1002/hbm.20720
*183 Grabner, R. H., Reishofer, G., Koschutnig, K., & Ebner, F. (2011). Brain correlates of mathematical competence in processing mathematical representations. Frontiers in human neuroscience, 5, 130. https://doi.org/10.3389/fnhum.2011.00130
*184 Schlaggar, B. L., & McCandliss, B. D. (2007). Development of neural systems for reading. Annual review of neuroscience, 30, 475–503. https://doi.org/10.1146/annurev.neuro.28.061604.135645
*185 Sliwinska, M. W., James, A., & Devlin, J. T. (2015). Inferior parietal lobule contributions to visual word recognition. Journal of cognitive neuroscience, 27(3), 593–604. https://doi.org/10.1162/jocn_a_00721
*186 Sestieri, C., Corbetta, M., Romani, G. L., & Shulman, G. L. (2011). Episodic memory retrieval, parietal cortex, and the default mode network: functional and topographic analyses. The Journal of neuroscience : the official journal of the Society for Neuroscience, 31(12), 4407–4420. https://doi.org/10.1523/JNEUROSCI.3335-10.2011
*187 Cabeza, R., Ciaramelli, E., & Moscovitch, M. (2012). Cognitive contributions of the ventral parietal cortex: an integrative theoretical account. Trends in cognitive sciences, 16(6), 338–352. https://doi.org/10.1016/j.tics.2012.04.008
*188 Bloechle, J., Huber, S., Bahnmueller, J., Rennig, J., Willmes, K., Cavdaroglu, S., Moeller, K., & Klein, E. (2016). Fact learning in complex arithmetic-the role of the angular gyrus revisited. Human brain mapping, 37(9), 3061–3079. https://doi.org/10.1002/hbm.23226
*189 Sokolowski, H. M., Hawes, Z., & Ansari, D. (2023). The neural correlates of retrieval and procedural strategies in mental arithmetic: A functional neuroimaging meta-analysis. Human brain mapping, 44(1), 229–244. https://doi.org/10.1002/hbm.26082
*190 Yeo, D. J., Wilkey, E. D., & Price, G. R. (2017). The search for the number form area: A functional neuroimaging meta-analysis. Neuroscience and biobehavioral reviews, 78, 145–160. https://doi.org/10.1016/j.neubiorev.2017.04.027
*191 Grotheer, M., Ambrus, G. G., & Kovács, G. (2016). Causal evidence of the involvement of the number form area in the visual detection of numbers and letters. NeuroImage, 132, 314–319. https://doi.org/10.1016/j.neuroimage.2016.02.069
*192 Daitch, A. L., Foster, B. L., Schrouff, J., Rangarajan, V., Kaşikçi, I., Gattas, S., & Parvizi, J. (2016). Mapping human temporal and parietal neuronal population activity and functional coupling during mathematical cognition. Proceedings of the National Academy of Sciences of the United States of America, 113(46), E7277–E7286. https://doi.org/10.1073/pnas.1608434113
*193 Starrfelt, R., & Behrmann, M. (2011). Number reading in pure alexia--a review. Neuropsychologia, 49(9), 2283–2298. https://doi.org/10.1016/j.neuropsychologia.2011.04.028
*194 Arsalidou, M., Pawliw-Levac, M., Sadeghi, M., & Pascual-Leone, J. (2018). Brain areas associated with numbers and calculations in children: Meta-analyses of fMRI studies. Developmental cognitive neuroscience, 30, 239–250. https://doi.org/10.1016/j.dcn.2017.08.002
*195 Peters, L., & De Smedt, B. (2018). Arithmetic in the developing brain: A review of brain imaging studies. Developmental cognitive neuroscience, 30, 265–279. https://doi.org/10.1016/j.dcn.2017.05.002
*196 Merkley, R., & Ansari, D. (2016). Why numerical symbols count in the development of mathematical skills: Evidence from brain and behavior. Current Opinion in Behavioral Sciences, 10, 14-20. https://doi.org/10.1016/j.cobeha.2016.04.006
*197 Butterworth, Brian & Reeve, Robert (2008). Verbal counting and spatial strategies in numerical tasks: Evidence from indigenous australia. Philosophical Psychology 21 (4):443–457. http://dx.doi.org/10.1080/09515080802284597
*198 Butterworth, B., Reeve, R., & Reynolds, F. (2011). Using mental representations of space when words are unavailable: studies of enumeration and arithmetic in indigenous Australia. Journal of Cross-Cultural Psychology, 42(4), 630–638. https://doi.org/10.1177/0022022111406020
*199 Horák, M., Uhrin, M., & Amaral, A. P. (2023). Status of the Current Scientific Knowledge on Pirahã: What is Known and What Could be Studied in Future?. Anthropologia Integra, 14(2), 25–33. http://dx.doi.org/10.5817/AI2023-2-25
*200 Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122(3), 371–396. https://doi.org/10.1037/0096-3445.122.3.371
*201 Hubbard, E. M., Piazza, M., Pinel, P., & Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nature reviews. Neuroscience, 6(6), 435–448. https://doi.org/10.1038/nrn1684
*202 de Hevia, M. D., Veggiotti, L., Streri, A., & Bonn, C. D. (2017). At Birth, Humans Associate "Few" with Left and "Many" with Right. Current biology : CB, 27(24), 3879–3884.e2. https://doi.org/10.1016/j.cub.2017.11.024
*203 Di Giorgio, E., Lunghi, M., Rugani, R., Regolin, L., Dalla Barba, B., Vallortigara, G., & Simion, F. (2019). A mental number line in human newborns. Developmental science, 22(6), e12801. https://doi.org/10.1111/desc.12801
*204 Göbel, S. M., Shaki, S., & Fischer, M. H. (2011). The cultural number line: A review of cultural and linguistic influences on the development of number processing. Journal of Cross-Cultural Psychology, 42(4), 543–565. https://doi.org/10.1177/0022022111406251
*205 Núñez, R. E. (2011). No innate number line in the human brain. Journal of Cross-Cultural Psychology, 42(4), 651–668. https://doi.org/10.1177/0022022111406097
*206 Cooperrider, K., Marghetis, T., & Núñez, R. (2017). Where Does the Ordered Line Come From? Evidence From a Culture of Papua New Guinea. Psychological science, 28(5), 599–608. https://doi.org/10.1177/0956797617691548
*207 Pitt, B., Ferrigno, S., Cantlon, J. F., Casasanto, D., Gibson, E., & Piantadosi, S. T. (2021). Spatial concepts of number, size, and time in an indigenous culture. Science advances, 7(33), eabg4141. https://doi.org/10.1126/sciadv.abg4141
*208 Núñez, R., Cooperrider, K., & Wassmann, J. (2012). Number concepts without number lines in an indigenous group of Papua New Guinea. PloS one, 7(4), e35662. https://doi.org/10.1371/journal.pone.0035662
*209 Vallortigara G. (2017). Comparative cognition of number and space: the case of geometry and of the mental number line. Philosophical transactions of the Royal Society of London. Series B, Biological sciences, 373(1740), 20170120. https://doi.org/10.1098/rstb.2017.0120
*210 Toomarian, E. Y., & Hubbard, E. M. (2018). On the genesis of spatial-numerical associations: Evolutionary and cultural factors co-construct the mental number line. Neuroscience and biobehavioral reviews, 90, 184–199. https://doi.org/10.1016/j.neubiorev.2018.04.010
*211 Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends in cognitive sciences, 7(11), 483–488. https://doi.org/10.1016/j.tics.2003.09.002
*212 Hamamouche, K., & Cordes, S. (2019). Number, time, and space are not singularly represented: Evidence against a common magnitude system beyond early childhood. Psychonomic bulletin & review, 26(3), 833–854. https://doi.org/10.3758/s13423-018-1561-3
*213 Hawes, Z., & Ansari, D. (2020). What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior. Psychonomic bulletin & review, 27(3), 465–482. https://doi.org/10.3758/s13423-019-01694-7
*214 Bates, K. E., Gilligan-Lee, K., & Farran, E. K. (2021). Reimagining mathematics: The role of mental imagery in explaining mathematical calculation skills in childhood. Mind, Brain, and Education, 15(2), 189–198. https://doi.org/10.1111/mbe.12281
*215 Hawes, Z., Sokolowski, H. M., Ononye, C. B., & Ansari, D. (2019). Neural underpinnings of numerical and spatial cognition: An fMRI meta-analysis of brain regions associated with symbolic number, arithmetic, and mental rotation. Neuroscience and biobehavioral reviews, 103, 316–336. https://doi.org/10.1016/j.neubiorev.2019.05.007
*216 Dehaene, S., & Cohen, L. (2007). Cultural recycling of cortical maps. Neuron, 56(2), 384–398. https://doi.org/10.1016/j.neuron.2007.10.004
*217 Benavides-Varela, S., Pitteri, M., Priftis, K., Passarini, L., Meneghello, F., & Semenza, C. (2014). Right-hemisphere (spatial?) acalculia and the influence of neglect. Frontiers in human neuroscience, 8, 644. https://doi.org/10.3389/fnhum.2014.00644
*218 Price, G. R., Mazzocco, M. M., & Ansari, D. (2013). Why mental arithmetic counts: brain activation during single digit arithmetic predicts high school math scores. The Journal of neuroscience : the official journal of the Society for Neuroscience, 33(1), 156–163. https://doi.org/10.1523/JNEUROSCI.2936-12.2013
*219 Rosenberg-Lee, M., Lovett, M. C., & Anderson, J. R. (2009). Neural correlates of arithmetic calculation strategies. Cognitive, affective & behavioral neuroscience, 9(3), 270–285. https://doi.org/10.3758/CABN.9.3.270
*220 Granà, A., Hofer, R., & Semenza, C. (2006). Acalculia from a right hemisphere lesion dealing with "where" in multiplication procedures. Neuropsychologia, 44(14), 2972–2986. https://doi.org/10.1016/j.neuropsychologia.2006.06.027
*221 Semenza, C., Salillas, E., De Pallegrin, S., & Della Puppa, A. (2017). Balancing the 2 Hemispheres in Simple Calculation: Evidence From Direct Cortical Electrostimulation. Cerebral cortex (New York, N.Y. : 1991), 27(10), 4806–4814. https://doi.org/10.1093/cercor/bhw277
*222 Salillas, E., Benavides-Varela, S., & Semenza, C. (2023). The brain lateralization and development of math functions: progress since Sperry, 1974. Frontiers in human neuroscience, 17, 1288154. https://doi.org/10.3389/fnhum.2023.1288154
*223 Furumoto H. (2006). Pure misallocation of "0" in number transcoding: a new symptom of right cerebral dysfunction. Brain and cognition, 60(2), 128–138. https://doi.org/10.1016/j.bandc.2005.10.002
*224 Benavides-Varela, S., Passarini, L., Butterworth, B., Rolma, G., Burgio, F., Pitteri, M., Meneghello, F., Shallice, T., & Semenza, C. (2016). Zero in the brain: A voxel-based lesion-symptom mapping study in right hemisphere damaged patients. Cortex; a journal devoted to the study of the nervous system and behavior, 77, 38–53. https://doi.org/10.1016/j.cortex.2016.01.011
*225 Haupt, M., Gillebert, C. R., & Demeyere, N. (2017). The zero effect: voxel-based lesion symptom mapping of number transcoding errors following stroke. Scientific reports, 7(1), 9242. https://doi.org/10.1038/s41598-017-08728-x
*226 Tablante, J., Krossa, L., Azimi, T., & Chen, L. (2023). Dysfunctions associated with the intraparietal sulcus and a distributed network in individuals with math learning difficulties: An ALE meta-analysis. Human brain mapping, 44(7), 2726–2740. https://doi.org/10.1002/hbm.26240
*227 Crollen, V., Seron, X., & Noël, M. P. (2011). Is Finger-counting Necessary for the Development of Arithmetic Abilities?. Frontiers in psychology, 2, 242. https://doi.org/10.3389/fpsyg.2011.00242
*228 Melzack, R., Israel, R., Lacroix, R., & Schultz, G. (1997). Phantom limbs in people with congenital limb deficiency or amputation in early childhood. Brain : a journal of neurology, 120 ( Pt 9), 1603–1620. https://doi.org/10.1093/brain/120.9.1603
*229 Tschentscher, N., Hauk, O., Fischer, M. H., & Pulvermüller, F. (2012). You can count on the motor cortex: finger counting habits modulate motor cortex activation evoked by numbers. NeuroImage, 59(4), 3139–3148. https://doi.org/10.1016/j.neuroimage.2011.11.037
*230 Pitt, B., & Casasanto, D. (2020). The correlations in experience principle: How culture shapes concepts of time and number. Journal of experimental psychology. General, 149(6), 1048–1070. https://doi.org/10.1037/xge0000696
*231 Andres, M., Michaux, N., & Pesenti, M. (2012). Common substrate for mental arithmetic and finger representation in the parietal cortex. NeuroImage, 62(3), 1520–1528. https://doi.org/10.1016/j.neuroimage.2012.05.047
*232 Lingnau, A., & Downing, P. E. (2015). The lateral occipitotemporal cortex in action. Trends in cognitive sciences, 19(5), 268–277. https://doi.org/10.1016/j.tics.2015.03.006
*233 Martory, M. D., Mayer, E., Pegna, A. J., Annoni, J. M., Landis, T., & Khateb, A. (2003). Pure global acalculia following a left subangular lesion. Neurocase, 9(4), 319–328.
※文献128以前は前回・前々回を参照。
