AtCoder Beginner Contest 330 振り返り

flower

昨日の振り返りです！

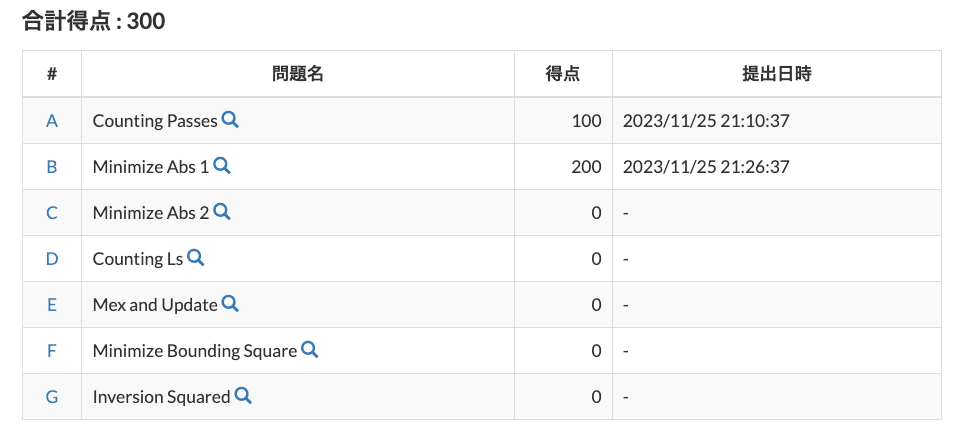
結果

C問題でWAが解決できずに終わってしまいました
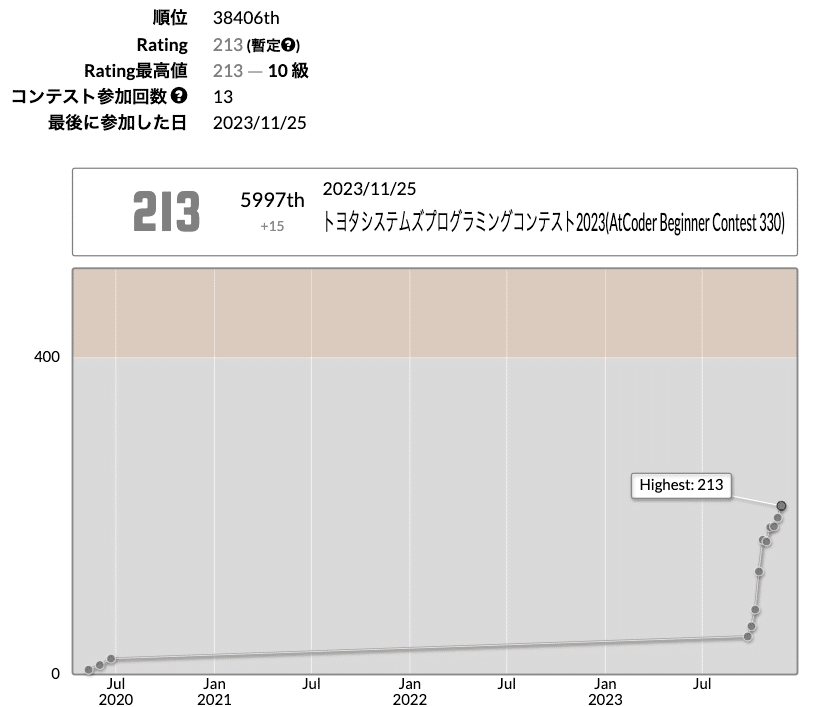
レーティングはちょっと上がったけど納得いかない

今回の結果
+15上がりました

各問題の振り返り

A - Counting Passes

ある値以上の要素をカウントする問題。
filterしてlengthするだけです。

main :: IO ()
main = do
  [_, l] <- readInputIntList
  as <- readInputIntList

  print $ length $ filter (>= l) as

B - Next

最初問題見た時「何これ？」なった問題です。（笑）
わかれば難しいことはなくて、入力値に対して絶対値が最も小さくなる値、つまり最も近い値を求める問題です。
$${A_i}$$ が $${L \le X \le R}$$の間にいる間は$${A_i}$$がそのまま回答になって、$${A_i \lt L}$$ の場合は $${L}$$ , $${A_i \gt R}$$ の場合は$${R}$$が回答になります。二分探索も考えましたが全探索で十分でした。

main :: IO ()
main = do
  [_, l, r] <- readInputIntList
  as <- V.fromList <$> readInputIntList

  putStrLn $ unwords $ V.toList $ V.map show $ findClosest l r as

findClosest :: Int -> Int -> V.Vector Int -> V.Vector Int
findClosest l r = V.map go
  where
    go a
      | a < l = l
      | a > r = r
      | otherwise = a

C - Minimize Abs 2

$${\vert x^2 + y^2 - D \vert}$$の最小値を求める問題。xを固定してyを二分探索で解けそうだなーと思ったんですが、何回やってもWAで終わってしまいました。。

main :: IO ()
main = do
  d <- readInputInt

  print $ findMinDiff d

findMinDiff :: Int -> Int
findMinDiff d = minimum [abs (x ^ 2 + y ^ 2 - d) | x <- [0 .. limit], let y = bSearch 0 limit (x ^ 2)]
  where
    limit = floor . sqrt $ fromIntegral d
    bSearch l h x2
      | h < l = h
      | otherwise =
          let mid = l + (h - l) `div` 2
              midVal = mid ^ 2
           in if midVal + x2 == d
                then mid
                else
                  if midVal + x2 < d
                    then bSearch (mid + 1) h x2
                    else bSearch l (mid - 1) x2

Xでnaoyaさんが平方数をあらかじめ生成して三分探索を使えば解けると言っていたので、この解法で解き直したところACになりました。

三分探索は凹凸型の関数の最小・最大値を求める時に使えるアルゴリズムで、今回のような$${\vert x^2 + y^2 - D \vert}$$の最小値を求めるケースに適用できます。(cyancyanさん教えていただきありがとうございました！)

実際に解いてみると実装は以下のようになります。

main :: IO ()
main = do
  d <- readLn @Int

  let xs = takeWhile (<= d) $ map (\i -> i * i) [0 ..]
      n = length xs
      ys = listArray @UArray (1, n) xs
      f d x y = abs (x + y - d)

      res = minimum $ concat [map (\i -> f d x (ys ! i)) (range result) | x <- xs, let result = trisect (1, n) (\i -> f d x (ys ! i))]

  print res

trisect :: (Int, Int) -> (Int -> Int) -> (Int, Int)
trisect (l, r) f
  | r - l <= 2 = (l, r)
  | f m1 > f m2 = trisect (m1, r) f
  | otherwise = trisect (l, m2) f
  where
    m1 = (l * 2 + r) `div` 3
    m2 = (l + r * 2) `div` 3

これだとACになりました。

全体を振り返って

C問題解けると思ったんだけどできなかったなあ…

おまけ

今回、何のテストで落ちているかがわからなかったのが敗因の一つなので、次回からプロパティベーステストを使いたいと思っています。
プロパティベーステストとは超ざっくり説明すると「プロパティに沿ってテストデータを自動生成する単体テスト」のことを指します。
実践プロパティベーステストも買ったので、これを読んで勉強しながら次に備えたいと思います！
https://www.lambdanote.com/collections/proper-erlang-elixir/products/proper-ebook


この記事が気に入ったらサポートをしてみませんか？