AtCoder Beginner Contest 326 振り返り
恒例の振り返りです。
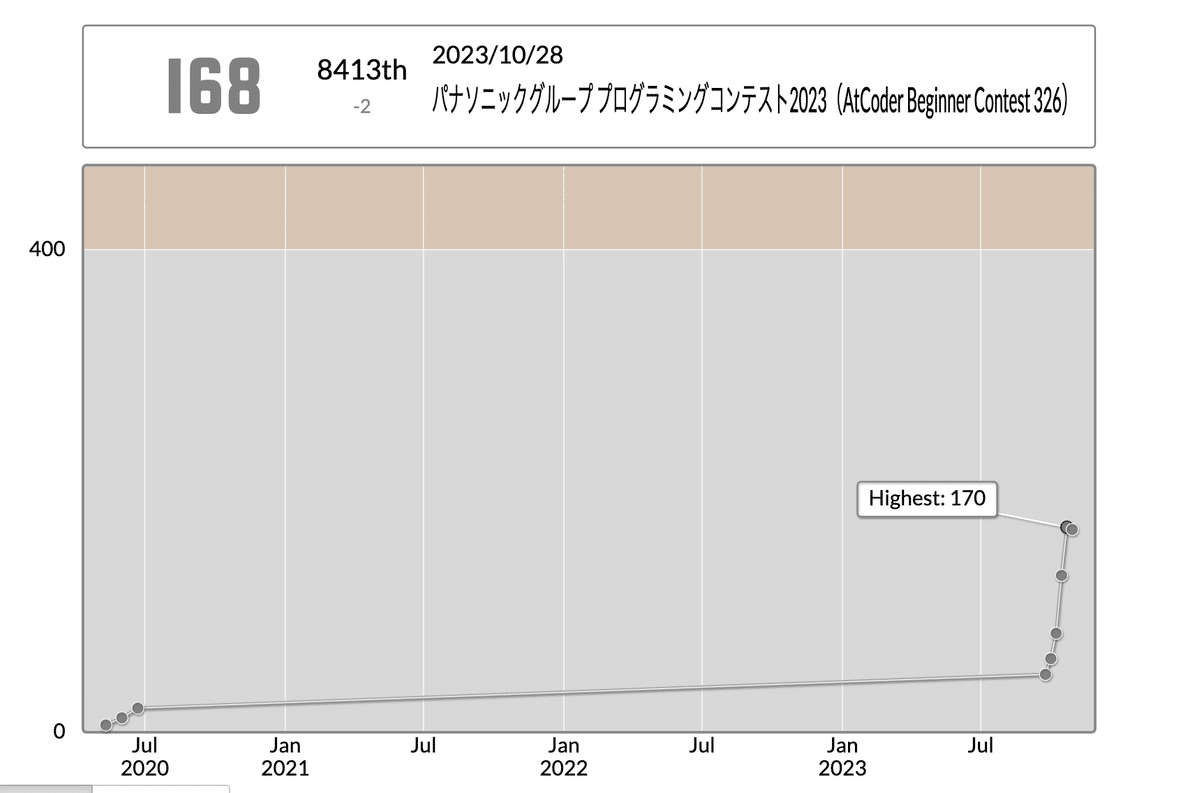
結果
今回はBまでしか解けませんでした。。

各問題の振り返り
A - 2UP3DOWN
ちょっとハマってしまいました…
main :: IO ()
main = do
(x, y) <- readPairInt
if (y > x) && (y - x <= 2) || (x > y) && (x - y <= 3) then putStrLn "Yes" else putStrLn "No"B - 326-like Numbers
これは特に問題なく解けました。divModが商と余りを同時に得られて便利。
main :: IO ()
main = do
n <- readInputInt
let listOf326Numbers = generate326Numbers
print $ minimum $ V.filter (>= n) listOf326Numbers
isLike326Number :: Int -> Bool
isLike326Number n =
let (hundreds, rest) = n `divMod` 100
(tens, ones) = rest `divMod` 10
in hundreds * tens == onesC - Peak(Upsolved)
今回残念ながら解けませんでした。尺取法と呼ばれる方法を使って解くのがセオリーなようです。
Haskellの尺取法はhttps://zenn.dev/osushi0x/articles/e5bd9fe60abee4が参考になりました。
main :: IO ()
main = do
(n, m) <- readPairInt
positions <- readInputIntList
print $ solve n m (VU.fromList $ L.sort positions)
solve :: Int -> Int -> VU.Vector Int -> Int
solve n m positions = shakutori 0 0 0 positions
where
shakutori :: Int -> Int -> Int -> VU.Vector Int -> Int
shakutori left right maxCount positions
| right >= n = maxCount
| otherwise =
let start = positions VU.! left
end = positions VU.! right
in if end - start < m
then shakutori left (right + 1) (max maxCount (right - left + 1)) positions
else shakutori (left + 1) right maxCount positionsちなみに二分探索でも解けます。
main :: IO ()
main = do
(n, m) <- readPairInt
positions <- readInputIntList
let sortedPositions = V.fromList $ L.sort positions
print $ countPresents m sortedPositions n
countPresents :: Int -> V.Vector Int -> Int -> Int
countPresents m positions n =
let findMaxPresents startPos =
let endPos = upperBinarySearch (startPos + 1) (n - 1) (positions V.! startPos + m)
in endPos - startPos
upperBinarySearch low high x
| low > high = low
| otherwise =
let mid = (low + high) `div` 2
in if positions V.! mid < x
then upperBinarySearch (mid + 1) high x
else upperBinarySearch low (mid - 1) x
in maximum $ map findMaxPresents [0 .. n - 1]全体を振り返って
今回全然だめだった。。実力不足なので練習します!
