
多数決で決めすぎてない?日常に役立つデータ収集のコツ
数学史上、最も美しい式をご存じだろうか。
いや、まさか知らないとは言わせない。聞けば誰もが思い出す。
e^iπ+1=0
いわゆるオイラーの等式である。
自然対数の底eと円周率πと虚数iと、1と0が贅肉なく一つの式に、あるべくしてあるように収まるこの公式は、もしもこの世に神様がいるとすれば、その最有力の証拠物件として挙げられる一品だろう。
数学が得意な阿良々木暦はこんな風に思う。
そんなわけで、今回は数学の物語だ。
数学と言うと構えてしまう向きもあるかもしれないので、砕いて算数の話と言い換えてもいい。
いっそもっと端的に、数の話と言ってしまっても。
なにせ、これは、数の多さで解が決まってしまう話。
即ち、多数決の話なのだから。
多数決。
間違ったことでも真実にしてしまえる、唯一の方法。幸せではなく、示し合せを追及する積木細工の方式。
不等式。
不当式。
オイラーの等式が、神の存在を証明できる証拠物品であるならば、多数決という不当式は人類が本当の意味で発明したとされる最も醜い式である。
こちらは私の好きな作家・西尾維新の作品からの引用です。言葉遊びが非常に巧みで、読んでいて深みを感じます。上の引用では、「オイラーの等式」という神の存在を証明しかねないほど美しい式と、反対に「多数決」という人類が生み出した最も醜い式が対比されています。
多数決に対するイメージ
皆さんは多数決についてどのような印象をお持ちでしょうか?
「決め事を楽に決められる便利な方法では?」という肯定的な見方もあるでしょう。逆に、「自分は納得していないけど、多数決の結果に従わなくてはならない経験がある」という人も少なくないはずです。
実際、私たちの身近には多数決があふれています。たとえば国民による多数決(選挙)で総理大臣や都知事が決まり、学校や職場のちょっとした意見調整も多数決で行われることがしばしばあります。国の運命を左右するような重大な選択から、ランチのメニューまで──私たちは日常的に多数決を使い、「人数の多さ」で可否を決めているのです。
しかし、ここには重大な問題があります。たとえば51対49であれ、51の意見が採用されてしまえば、残り49の意見は事実上無視される。この構造こそが「多数決」の正体です。まさに引用部分にもあるように、「間違ったことでも真実にしてしまえる、唯一の方法」なのかもしれません。
人数による決定と、論理による決定
ここまで長い導入をしたのは、「人間社会は人数に基づいて決定が下される一方、数学や論理の世界では合理性や論理性で真偽が決まる」という対比を示したかったからです。オイラーの等式は、神をも証明しかねないほど美しい「等式」。対して多数決は、人類が発明した「不当式」とすら言えるかもしれない。
ここでは、人数ではなく科学的・論理的な手法で「真」を導くプロセスに注目してみたいと思います。すなわち、「多数決では決められない」場面でどのような方法が用いられているか──科学論文や研究の場で信頼性を確保するための手法を簡単に紹介しましょう。
🐑信用できるデータを集めるには?
多数決であれば「賛成する人の数=データの大きさ」がものをいいますが、それが本当に“正しさ”を担保しているとは限りません。どのようにデータが集められたかに偏りがあれば、結果は大きく歪められてしまいます。
たとえば、クラスの委員長選出を多数決で行うとき。候補者の1人が多くの友人を抱えていれば、あらかじめ話を合わせることで有利に票が集まるかもしれません。科学的な研究でも同じで、データ収集が偏っていれば、どんなに大規模な調査でも信頼度は疑わしいものになります。
多数決では単に“人の数”で決まってしまうが、科学では“どんな人をどのように抽出するか”が極めて重要になる。
そのため、科学的論文では「どうデータを集めるか」を非常に重視します。統計学者のフィッシャーが提案したフィッシャーの三原則(繰り返し・無作為化・局所管理)は、こうした偏りを最小限に抑えるための基本的な指針です。
フィッシャーの三原則がなんであるかイメージしやすいよう簡単に説明を加えると
繰り返し :同じ実験やデータ収集を何度も行い、結果の再現性を確保する。
無作為化 :調査対象をランダムに選ぶことで、偏りを最小限にする。
局所管理 :同一条件下でデータを収集し、外部要因の影響を排除する。
これらを意識することで、偏りや誤差の入り込む余地を減らし、より“信用できる”データを得ることが可能になります。
もっと詳しいこと知りたい方はこちらのwikiを参照ください。
こちらのは私が書いたnoteなのですがこちらでのデータ収集もこれを意識したものになっています。
ハッシュタグをなるべくジャンルがかぶっていないようにランダムに選び検証。
ハッシュタグの変更以外は同じ条件(日時、記事数、急上昇50以内であること)に統一しデータを収集。
繰り返しについては毎日同じ時間(局所管理)にデータを収集を行うことで比較する上で信用できるデータになります。
🐑実際どのような「調べ方」があるの?
データ収集での“人数”が多いこと自体は意味がありますが、それが「ランダムに」「公平に」選ばれた人数であるかどうかが重要です。代表的なサンプリング手法を3つ挙げてみます。
単純無作為抽出
単純無作為抽出というのは、「くじ引き」のようなやり方で調べたいものを選ぶ方法です。
データを収集したい対象が膨大な時すべてのデータを収集するのは大変な場合、この手法を使って調べる対象の数を減らし、ランダムに調査対象を選ぶ。
このランダムな抽出によって調査対象の対象である人が皆同様に選ばれる可能性があるようにする方法が単純無作為抽出です。

系統抽出法
系統抽出法は、「等間隔で選ぶ」方法です。「とび縄式」や「階段式」の選び方とも言えます。
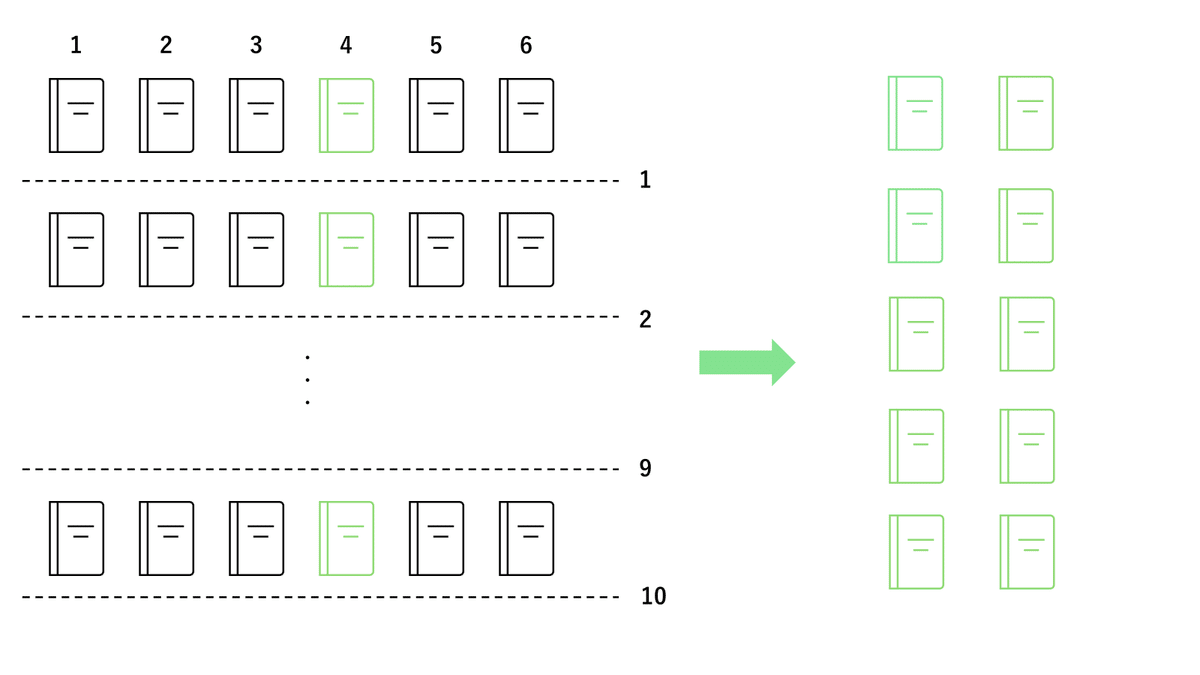
例えば、書類をずらっとナンバリングして並べたうえで、4番ごとに1枚取り出すことで手軽に全体をバランスよくサンプリングすることができます。
層化抽出法
層化無作為抽出法は、「グループに分けてから選ぶ方法」です。
男女比や地域差を考慮して、全体の比率に応じてサンプル数を決めることでどのグループからも平等に意見を扱うことができます。

🐑いろいろな選び方とその使い方
単純無作為抽出(くじ引き方式)
とにかく公平に、特別な条件がない場合に
例:クラスの代表をくじ引きで決める
系統抽出法(とび縄方式)
順番に並んだ対象が大量にある場合、手軽に全体をバランスよくサンプリングしたい場合
例:大量の資料や図書の中から間隔を空けて抽出する
層化無作為抽出法(グループ分け方式)
重要なグループの意見を確実に含めたいとき、異なる層のバランスを取りたいとき
例:男女別・学年別・地域別など、セグメントがはっきりある場合
大切なポイントは以下の2点です。
目的に合った方法を選ぶ
できるだけ公平・ランダム性を保つよう注意する
たとえば、
「何でもいいから一つ選ぶ」 → くじ引き(単純無作為抽出)
「順番どおりに並んでいる対象から効率的に拾いたい」 → とび縄方式(系統抽出)
「バランスよく選びたい」 → グループ分け(層化抽出)
目的や状況に合わせて最適な手法を選ぶことが、信頼度の高いデータを得るうえで重要です。
🐑まとめ
「最も美しい式」と評されるオイラーの等式は、神秘的なほどの調和を秘めています。それと対照的に、ほんの僅差であっても勝敗が決まる多数決は、ある種の「醜さ」をはらみながらも、私たちの社会を動かしてきた現実があります。
けれど、正しさを追求するためには、単純な人数の論理に頼るだけでは不十分です。データをどう集め、どう分析するかといった科学的アプローチが、不確かさを補い、より公正な視点をもたらしてくれます。
「美しさ」と「醜さ」の間を行き来しながら、人間は自らの社会を形作ってきました。私たちが意思決定をする際にも、ただ数に任せるだけでなく、論理やデータを活かし、新たな調和点を見出していくことが求められているのかもしれません。
