1993年のJリーグのレーティング推移
これまでで、イロレーティングとグリコレーティングについて学び、計算することもできるようになりましたので、実際に1シーズンを通してレーティングの算出をして、その推移を見てみたいと思います。
使用したデータはJリーグ初年度の1993年のリーグ戦の試合結果です。
イロレーティングの推移
算出方法は、レーティングの初期値が1500、変動係数Kの値は20に設定してあります。
得点差やホームアドバンテージは考慮していない、いわゆるオリジナルの計算方法です。

グラフを見ると、最初の方は徐々に差が広がっていくのがわかります。
なお、9月から10月の間はリーグ戦の中断期間だったため、変動がありません。
グリコレーティングの推移
算出方法は、レーティングは初期値が1500、レーティング偏差の初期値は350、レーティング偏差の減衰を表すcの値は、1ピリオド15日として2年間で50から350に戻るという計算で、c=約49.7に設定してあります。
こちらも、得点差やホームアドバンテージは考慮していない、いわゆるオリジナルの計算方法です。

グリコレーティングで算出した結果は、イロレーティングとは大きくちがって、激しく変動しています。
レーティング偏差が最大値から始まっているため、開幕直後は、特に大きな変動になっています。
その後、変動はだんだん落ち着いてきますが、9月から10月の中断期間後には、また少し変動が大きくなります。試合が無いため、レーティング偏差が時間経過とともに大きくなったのがわかります。
イロレーティングとグリコレーティングの比較
上位、中位、下位の3チームを抜き出して、イロレーティングとグリコレーティングの推移の比較をしてみます。
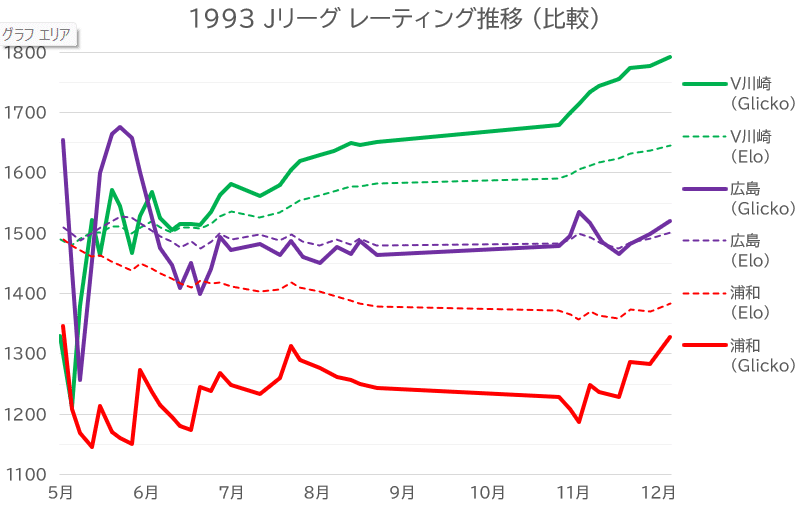
破線がイロレーティング、実線がグリコレーティングです。
中位の広島の推移は、序盤を除いて、どちらの算出方法でもほとんど変わりませんが、一方、上位のV川崎や下位の浦和は差が大きくなっています。
イロレーティングの動きが鈍いのか、あるいは、グリコレーティングの動きが激しすぎるのか、それとも両方か、検証の必要がありそうです。
