損失関数を使ってレーティングの正確性を評価してみる
これまでで、どの種類がより正しいレーティングかなのかを検証するには、「損失関数」なるものを使えばよいことがわかりました。
今回は、レーティングの値と実際の結果を基に、損失関数を使って計算して、比較していきます。
使った損失関数とデータ
平均絶対誤差 (MAE: Mean Absolute Error)
平均二乗誤差 (MSE: Mean Squared Error)
ロジスティック損失関数 (LogLoss)
これらのうち、LogLossについては、結果が0か1かのどちらかの場合に適用できる手法なので、試合結果のうち引き分けを除外して算出することにしました。
データは、1993年から1998年までのJリーグのリーグ戦。
試合前のレーティングの差から求めた期待勝率を予測値、実際の試合結果の勝ち(1)・引き分け(0.5)・負け(0)を正解値として、計算しています。
評価結果(基本の4種類+固定)
これまで算出してきたイロレーティング(Elo)、グリコレーティング(Glicko)、および、それぞれ得点差とホームアドバンテージ加味したバージョン(Elo+, Glicko+)の4種類と、レーティングを一切変化させない1500固定バージョンを追加して比較してみました。
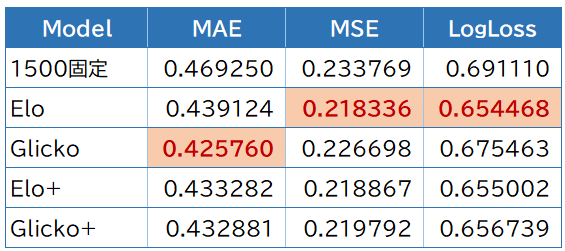
数値を縦に見比べた時に、より小さい値ほど誤差が少ないので、良いモデルと言えます。
赤色になっている数値が、各損失関数の中で最も良い値が出たものです。
1500固定が、当然ながら一番悪い値となっています。
平均絶対誤差(MAE)でも平均二乗誤差(MSE)でもロジスティック損失関数(LogLoss)でも最低値になっていることから、どの損失関数を使っても正しく評価できていることがわかりますし、レーティングを算出するどのモデルを使ったとしても、何もしないよりは良いということがわかります。
意外にも、得点差とホームアドバンテージを考慮したバージョン(Elo+, Glicko+)は、この中で一番良いモデルとはなれませんでした。
一番良かったのは、平均絶対誤差(MAE)ではオリジナルのグリコレーティング(Glicko)、平均二乗誤差(MSE)とロジスティック損失関数(LogLoss)では、わずかの差でオリジナルのイロレーティング(Elo)となりました。
評価結果(EloのKの値20~50)
次に、イロレーティング(Elo, Elo+)について、変動係数であるKの値を20~50の10刻みで変えて、比較してみました。
上で算出したイロレーティングはKの値を20にしてありましたので、新たに30, 40, 50を追加しました。

平均絶対誤差(MAE)では、Kの値を大きくすればするほど、数値が小さくなるので、良いモデルとなっています。
平均二乗誤差(MSE)とロジスティック損失関数(LogLoss)では、オリジナルではKが30、得点差とホームアドバンテージをつけた (+) ものではKが20のものが良いモデルとなっています。
また、MSEとLogLossは数値こそ違うものの、モデルの評価順は同じで、似たような指標であることがわかります。
評価結果(GlickoのRDの初期値100~350)
次に、グリコレーティング(Glicko, G+)について、レーティング偏差(RD)の初期値および最大値を350, 250, 200, 150, 100と変えて、比較してみました。
最初に算出したグリコレーティングのRD値は350でしたので、新たに250, 200, 150, 100を追加しました。
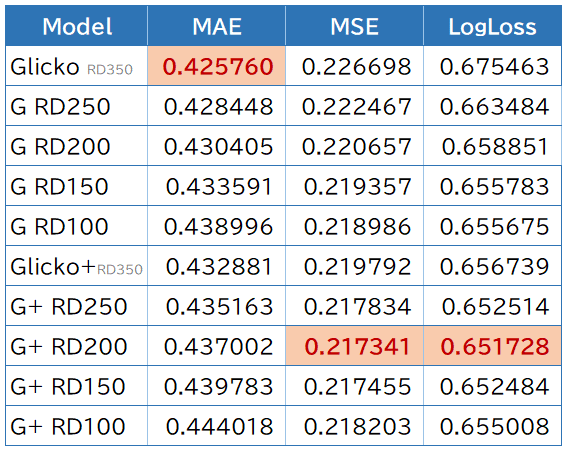
MAEでは、変動幅が大きくなるRD350のオリジナルバージョンがお気に入りのようです。
MSEおよびLogLossでは、+の付いていないオリジナルだとRD100、得点差等を考慮したバージョンですと、RD200あたりが最も良い数値となりました。
また、G+ RD200の数値は、今回算出したMSEおよびLogLossでは最も良い値になりました。
今回のまとめ
レーティングを一切変化させないバージョンと比べることで、損失関数を使ったレーティングモデルの比較が有効であることがわかりました。
平均絶対誤差(MAE)は、他の2つの損失関数とは違っていました。
感覚的なことですが、MAEはあまり正確な指標とはなっていないような気がします。
平均二乗誤差(MSE)とロジスティック損失関数(LogLoss)は、数値こそ違いますが、指標としては同じようなものであることがわかりました。
LogLossでは引き分けを無視していますので、たいして変わらないのであれば、今後は平均二乗誤差(MSE)だけの算出で問題なさそうです。
