統計検定2級②

まずは①を見てから

【超重要】標準化とは

Zにすることではあるが
本来は平均0、分散1にすること

【超重要】棄却する場合

①棄却域に入っている時
②信頼区間から外れる時

片側か両側か判断する時

変動係数とは

標準偏差÷平均

推定量の分散

一致推定量、標本分散と不偏分散(不偏推定量とも言う)

一致推定量とは

取る値が、母集団と一致するような値

不偏分散(不偏推定量)とは

毎回違う値を取るけど、推定量の平均が母集団と一致するような値

不偏推定量(不偏分散)を求める計算(覚えなくても良い)

分散、共分散と期待値の関係(超基本)

和と差の確率変数の性質

【例題】

【Iに関して】
UとVの平均は等しい👉⭕️

U=X+Y, V=X-Yで、XとYはどちらも平均が等しいので、UとVの平均も等しい

【IIに関して】
分散1＝分散2のときのみ、UとVは互いに独立である
👉⭕️

「UとVが独立」＝　「UとVの相関係数が0である」
相関係数の分子は、分散1ー分散2
↓
つまり分散1＝分散2であれば、相関係数は0になる！

【Ⅲに関して】
分散1と分散2の値によらず、UとVは同じ分布に従う
👉⭕️

まず、UとVは平均が同じ
また、分散に関して
V(U)＝V(x+y)＝V(x)+V(y)+2cov(xy)
V(v)＝V(xーy)＝V(x)+V(y)ー2cov(xy)
さらに、xとyは独立なのでcov(xy)は0

よって、V(U)＝V(v)

t値とは

標本をとったときのZのこと

t値から考えて、棄却する場合

①「t分布のパーセント点」から、自由度•有意水準からt値を導き、信頼区間に入ってない時

②棄却域に入る場合

自由度とは

自由に動ける変数の数のこと

サンプルサイズn=10をとっただけ👉自由度は10
n=10をとり、標本平均が確定した後👉自由度は9
↓
なぜなら、標本平均が確定したら、９個のデータを決めると残り一つも確定するため

P値(P−値とも表記する)とは

母集団の中で、信頼区間の外側にある確率のこと

P値から考えて棄却する場合

①p<有意水準のとき
②「標準正規分布の上側確率」よりP値を導き、
p<有意水準のとき
③P値から逆算して、「標準正規分布の上側確率」よりt値を導く。そして信頼区間に入っていないとき

F値とは

一元配置分散分析からF値を導く場合

F値から考えて棄却する場合

◯上側のみを考える場合
分散分析(３つ以上の標本があるとき)を考えるなら、「有意水準5%」と言われたら上側の5%を考える

◯上側と下側両方を考える場合
等分散性(2つの標本のみがあるとき)を考えるなら、「有意水準5%」と言われたら上側&下側2.5%を考える
👇
上側2.5%を考える時、普通にf分布の%表を参照すれば良い
下側2.5%を考える時、Fを1/F(逆数)にして、f分布を見る時も自由度を逆にして参照すれば良い

確率変数の差(X-Y)に関する確率

X＝ある年の6月の電気料金、Y＝前年の電気料金

P(X-Y≧800)を考える
これは平均0(なぜならXもYも平均同じだから、X−Yの平均は4000-4000)
さらに標準偏差500同士なので…

Pが未知の場合の処理の仕方(難)

(例)

①まずは二項分布のZを求めて、1.96で挟む
②信頼区間の幅を求める
③この幅にp(1-p)/nが含まれているが、このp(1-p)は最大が0.5×0.5で0.25となる。故に、分子が最大の時でも6%以下になるようなnを求めれば良い

母比率の推定値

(例)

母比率の推定値とは

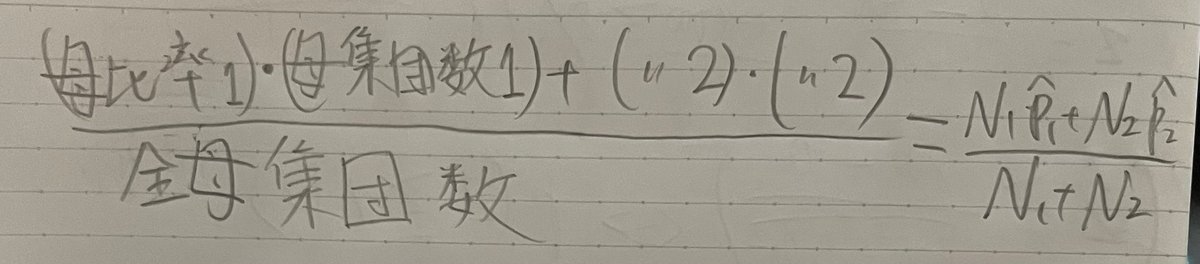
母比率の推定値の標準誤差とは

母比率(母平均)の差の信頼区間、t値

通常の信頼区間を求めるときは…

母比率(母平均)の差の信頼区間を求めるとき

①分散が既知の場合

【例題】

(キーポイント)
「非常に関心がある」と答えた割合に差があるかを検証している

まずは信頼区間を求めて、この信頼区間で「差がない」を表す「0」があるかどうかを検証するべきである

②分散が未知の場合

過誤

第一種の過誤

間違って帰無仮説が正しくなること

第二種の過誤

間違って対立仮説が正しくなること

カイ二乗検定

次のようなヒストグラムが来たら、まずはクラス集計表を書く必要がある

回帰分析

残差を全て均一にして関数にしたもの
つまり、残差の平均は0である

✅残差＝(元のデータ)ー(予測値の平均)

⭐️回帰分析での自由度の求め方

パラメータの自由度👉1を引くだけ
残差の自由度👉標本数からパラメータ引く

回帰分析でのt値の求め方(回帰係数の信頼区間の求め方につながる)

単回帰モデル•重回帰モデルの見方

最小二乗法

✅Interceptは切片を表す

「Interceptは定数項β0を表す」とあるが、14.3931＝β0の値である

0.4121＝β1の値である
つまり、total.incomeが1増えるごとに全体が0.4121増えることを表す

✅Pr(>|t|)はPー値を表し、有意水準を下まわれば、0ではないことが証明される

この場合の帰無仮説は、普通明記されないが
「各パラメータは0である」になる
👇
そのため、棄却すれば0ではない、つまり「パラメータは存在する」となる

ローレンツ曲線と完全平等線、ジニ係数

ローレンツ曲線から遠い＝ジニ係数が大きい＝不平等

ラスパイレス係数

抽出法

☑️単純無作為抽出法
全ての母集団から無作為に抽出

☑️系統抽出法
全ての母集団から、決まったルールで抽出

✅層化抽出法
互いに被ることのないグループに分けて、各層から無作為に抽出

✅集落(クラスター)抽出法
互いに被ることのないグループに分けて、各層の全てを抽出

○二段抽出法
二段階に分けて抽出する方法
例えば、最初は全国区で調査して、その後に地域ごとに調査するなど

研究の形態

✅観察研究
調査対象に介入をしない
(例)
国公立大に進学した人、私立大に進学した人の費用を調査

✅実験研究
介入を行う
(例)
ある病気の患者を2グループに分け、新薬と旧薬の効果の違いを観察

フィッシャーの三原則

無作為化

制御できない要因の影響を、偶然誤差に変えられる

繰り返し

同一の条件で、1人もしくは複数人の被験者のデータを取ること

局所管理

「実験条件」を同じようにして、各ブロックにわかること