確率分布と統計的推測(統計検定2級①)
確率変数とは
確率の集合のこと
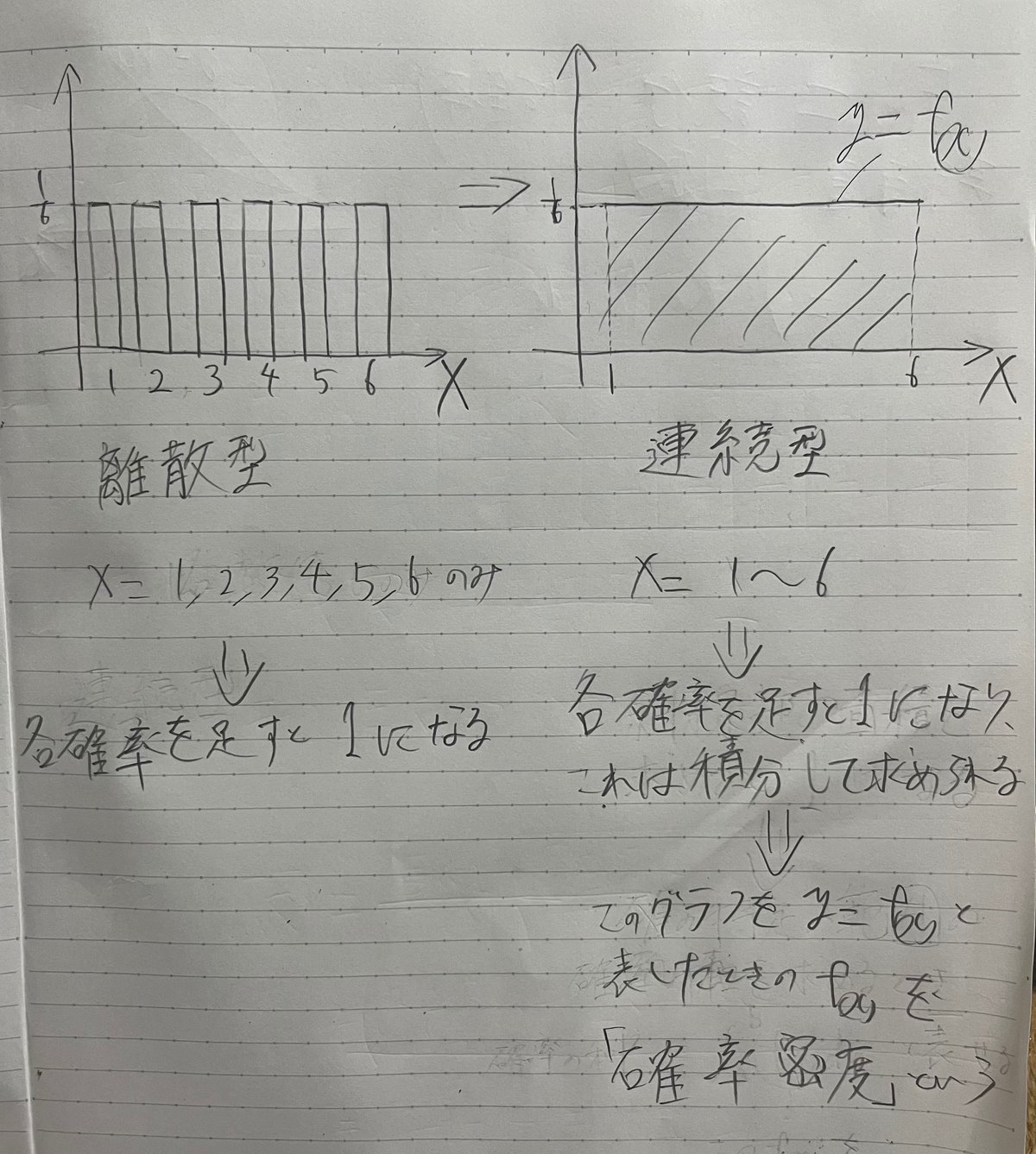
確率変数で、期待値の求め方

分散と期待値の関係(超基本)

和と差の確率変数の分散(公式)


二項分布とは


正規分布、標準正規分布
二項分布で、nを無限大まで飛ばすと、正規分布に近づく

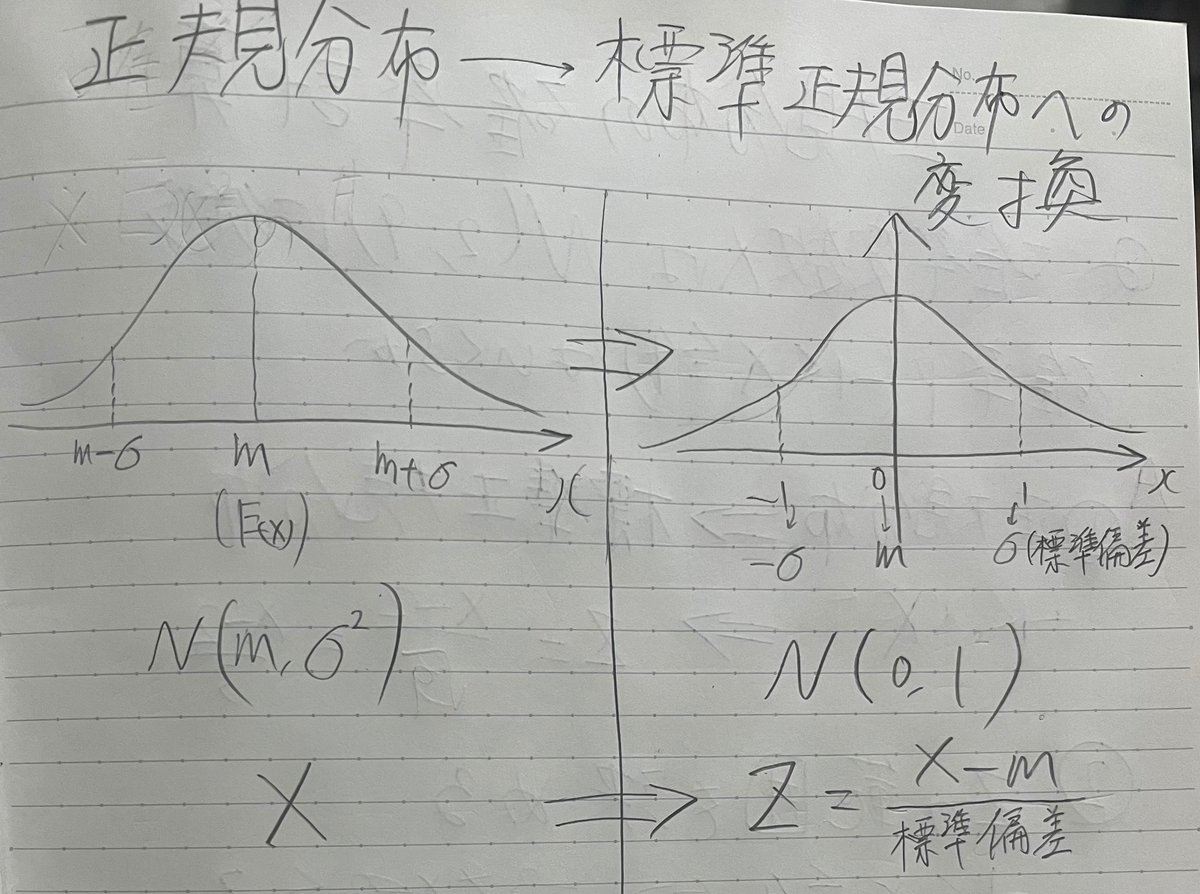
標準化(正規分布→標準正規分布への変換)
【標準化とは】
平均0標準偏差1の値Zに変えることである
標準正規分布の確率計算、上側確率の表の使い方

上側確率の表は、左の行が少数第一位、上の列が少数第二位を示す
↓
なので、例えばP(Z≧0.67)を求めたい場合、
左側の06、上側の0.07が交差するところを参照すれば良い

正規分布の確率計算

母集団と標本
✅母集団=全ての集団
☑️標本=母集団から一部をとったもの
✅母平均=母集団の中の平均
☑️標本平均=標本の中の平均
信頼区間 ①②
①標本平均(標本比率)の中で明らかな外れ値を除いたときの、母平均(母比率)の範囲
あくまで母平均(母比率)の範囲なので、
(標本平均)+1.96×(標本平均の分散)のように標本平均で評価をする

②母平均(母比率)の中で明らかな外れ値を除いたときの、標本平均(標本比率)の範囲
あくまで標本平均(標本比率)の範囲なので、
(母平均)+1.96×(母平均の分散)のように母平均で評価をする

Zを求めて、「標準正規分布の上側確率」からZの範囲を求める↓
そこから標本平均or母平均の範囲を求める
✅標本平均の分散=母分散/標本数
①母平均の信頼区間 例題

標本平均(標本比率)の信頼区間 例題


その他の関連例題

①Zの分母を先に計算する
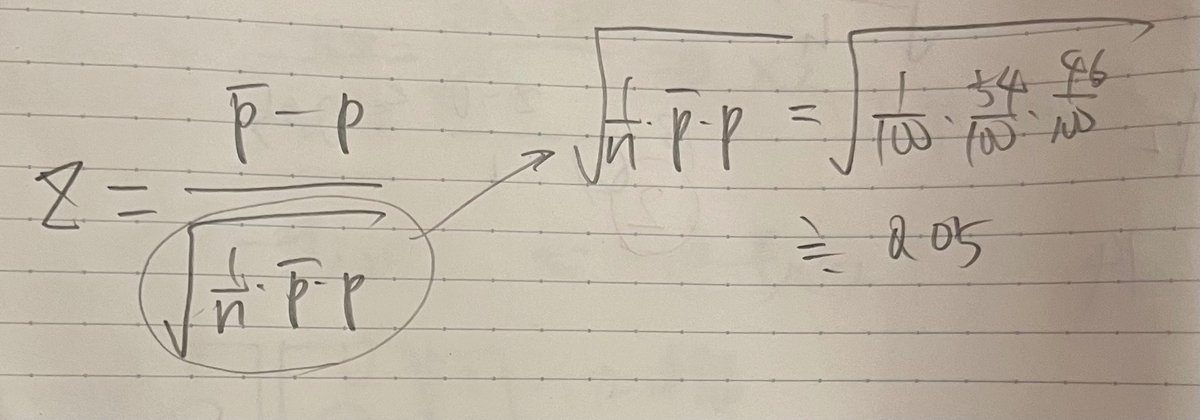
②Zの分子≦0.1なので、そこからZの範囲を求める

③よって、Z≦2となる確率を「標準正規分布の上側確率」より求める
終わり
【おまけ】
✅母平均は、期待値と同じになる
✅母平均=標本平均の期待値=いつも通りの確率だったら取れそうな値
この記事が気に入ったらサポートをしてみませんか?
