
球体そのもの以外に恐れるものはない
地球は球体であるという証拠がいくつもあります。なぜ地球平面論者は球体を恐れるのでしょうか? 1990 年の NASA のガリレオ宇宙探査機や 100 年以上前の地図には、南極が南極点にある大陸として明確に示されています。地球が球体であることは、さまざまな証拠によって裏付けられています。
ジョン・ギデオン・ハートネット 2024年7月11日

上の写真は、1990 年に NASA のガリレオ宇宙探査機が撮影した写真から合成された南極大陸全体の合成写真です。地球平面説を信じる多くの人々が主張しているように、探検家が南極点に到達するのを巨大な氷壁が妨げているという証拠は見当たりません。しかし、地球平面説を信じる人々は、NASA が発表するものは何も信用できないとも言います。

その結果、私はインターネットで 1950 年以前に作成された南極の地図がないか探してみることにしました。つまり、宇宙飛行や衛星の時代以前に作成された地図ということです。大陸全体を示すそのような画像をいくつか見つけましたが、その多くは iStock などの企業からのものであり、著作権の対象となっているため、ここで再現することはできません。画像検索は自分で簡単に行うことができます。

しかし、さらに遡って調べてみると、1900 年以前の地図帳の画像が見つかりました。そこには、南極大陸を含む球状の地球全体の地図が載っています。ここに示した地図帳「Illustrirter Hand-Atlas der Geographie und Statistik」は、トラウゴット・ブロムが編集し、1862 年にクライス & ホフマン社からドイツ語で出版されました。

これは、1900 年以前に、陸地や海の島々を地図に描いた船乗りたちの記録から、南極大陸を含む全世界の地図を作成した地図製作者が多数いたことを意味します。南に氷の壁がある平面地球は示されていません。平面なのは地図が印刷されているページだけで、球形の惑星を平面のページに投影するために使用されます。
では、地球が球体であることの何がそんなに重要なのでしょうか? 地球平面説を信じる人々はなぜ球体をそれほど恐れるのでしょうか? 彼らは「球体そのもの以外に恐れるものはない」と言います。
球体の物理学
インターネット上では、高性能なニコンのカメラで水面越しに見た建物、例えばミシガン湖越しに見たシカゴなどが、地球が平らであることを証明していると主張する人々がいる。
残念ながら、水上では、大気の高度に応じて温度が変化するため、レンズ効果が発生し、光が水面上で曲がる蜃気楼効果も発生します。
時々、見る人から少し離れたところで船の一部が地平線の下に隠れている画像が示されることがありますが、これは地球が球形であるという説を否定するものです。実際には、その逆で、海が球面上に広がっていることを示しています。

これは、海面が球状であることを示す良い例です。背景の船は、見える水平線の下に沈んでいます。船の甲板に積み上げられた輸送コンテナは見えますが、船体は見えません。明らかに、手前の船とは対照的です。手前の船は、はるかに近くにあるため、水中に沈んでいるように見えます。これは簡単に説明できます。
まず、球体の幾何学から始めましょう。

図 1 を使用して、海面に立っていて、高さがh (足元から目まで) で、海を眺めていると想像してください。遠くにある海面からの高さtの建物 (または船) がちょうど地平線上にあるのが見えます。建物 (または船) はtよりも高いかもしれませんが、それはあなたが立っている場所から地平線上にちょうど見える点です。建物 (または船) が見えない場合は、上の画像で遠くの船の船体によって示されているように、地平線の下にあります。
測定(レーザー測距装置を使用)により、見える建物(または船)までの距離がわかります。図 1 では、距離はd + Dと表されています。距離dは、目から直線がちょうど海面に触れる点、つまり海面に接する点までの距離です。距離Dは、同じ点から、海面、つまり地平線上にちょうど現れる建物(または船)の点までの距離です。
距離d は身長によって異なり、距離D は海抜の建物(または船)の高さによって異なります。
地球の半径は図 1 でRとして示されています。地球は球体で、実際には惑星の急速な自転により赤道に潮汐の膨らみがある扁平楕円体です。したがって、図 2 に示すように、その半径は赤道の最大半径約a = 6,378 km (3,963 マイル) から極の最小半径約b = 6,357 km (3,950 マイル) までの範囲です。以下を参照してください。

縮尺は正確ではありません。出典: Wikipedia
ピタゴラスの基本幾何学から、図 1 を使用して次の式を書き表すことができます。
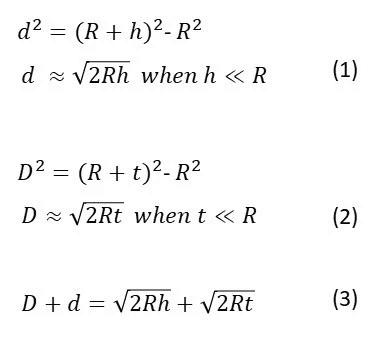
海抜高度hと建物(または船)の高さtは惑星Rの半径よりもはるかに小さいため、正確さを損なうことなく上記の近似値を簡単に算出できます。
式 (3) を使用すると、地球の曲率をテストできますが、前述のように、大気中の熱レンズ効果により、通常予想されるよりも遠くの地平線を見ることができます。ただし、この効果は曲率の議論を強化します。仮想の平面地球ではレンズ効果はなく、原則として制限なく見ることができるはずです。
FE論者は、球形の地球の赤道上半径に基づいて、曲率は地平線から1マイルの2乗あたり8.27インチずつ下がるはずだとよく言います。彼らが使用する単位は非常に扱いにくいですが、数字は正しいです。上記の式から、次のことがわかります。

どちらの場合でも、高さhから距離d 2まで、または地平線t上に見える建物 (または船) の高さから距離D 2までは同じであり、地球の直径の逆数、または定数である半径の 2 倍 (2 R )に等しくなります。これが明確であることを願っています。
これをテストするには、地平線からちょうど見える、異なる距離Dにある高さtが既知の一連の建物が必要になります。または、異なる距離にある高さが既知の船を使用することもできます。
これまで私が見た限りでは、測定値は球体惑星の予想とすべて一致しています。しかし、海上の空気の屈折率の変化によるレンズ効果により誤差が生じるでしょう。
しかし、惑星の半径を測定するにはもっと良い方法があります。紀元前 200 年、エラトステネスは現代のニコンのカメラなしでそれを行いました。私の図解による説明はここをご覧ください。
式 (4) の 1 マイルの 2 乗あたり 8.27 インチという数字は、地球の半径の尺度です。しかし、地球が実際に平らであれば、式 (4)の R は無限大に設定できます。つまり、この 8.27 という数字はゼロになります。まったく低下はありません。しかし、海上の船舶は明らかにそれを否定しており、海面は球面に従います。これがジオイドと呼ばれるものです。私の図解プレゼンテーションの 50 分あたりから始まる部分をご覧ください。
では、地球平面論者が球形の惑星に対して抱く恐怖とは何でしょうか?
球体そのもの以外に恐れるものは何もありません!
