
統計検定凖1級ワークブック 第3章:分布の特性値
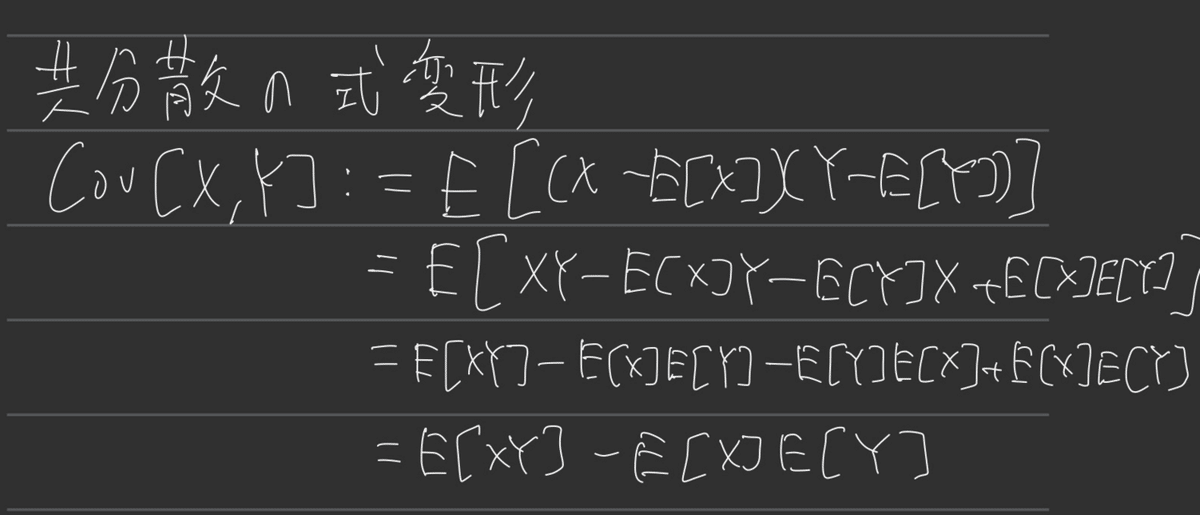




不偏分散は、標本分散と違い、期待値を取ると母分散になって嬉しいらしい。

分散共分散行列は確率変数が多次元のときに、その分布がわかるものらしい。(自分でも非常にぼやけたイメージしか湧いてない)
以下がおいおい分かりやすくなってくるんだろうなと思えた。
公式、法則、定理を導出、証明しまくった。確かに計算練習にはなったが、本番は逐一導出する時間がないし、今導出するにもかなり時間を喰う。それだけの価値があるといいな

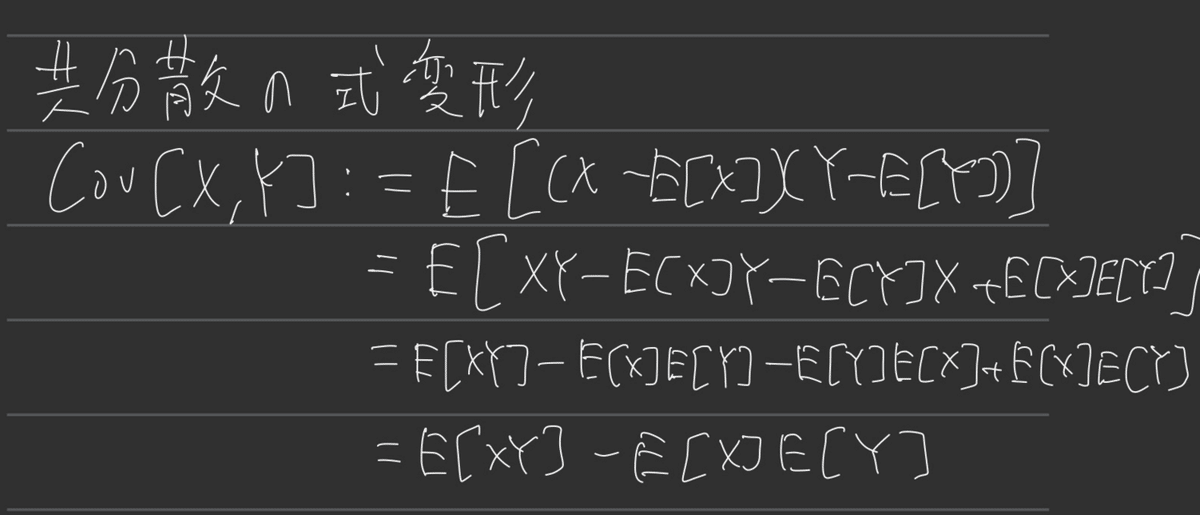




不偏分散は、標本分散と違い、期待値を取ると母分散になって嬉しいらしい。

分散共分散行列は確率変数が多次元のときに、その分布がわかるものらしい。(自分でも非常にぼやけたイメージしか湧いてない)
以下がおいおい分かりやすくなってくるんだろうなと思えた。
公式、法則、定理を導出、証明しまくった。確かに計算練習にはなったが、本番は逐一導出する時間がないし、今導出するにもかなり時間を喰う。それだけの価値があるといいな