見出し画像

ベイジアンネットワーク~因果の流れを捉えて予測する～

sogachin3

1. はじめに

　今回の記事ではベイジアンネットワークについて学んだことのアウトプットに挑戦しました。本記事の内容に関する間違いがあれば、ぜひご指摘いただけれると嬉しいです。
　統計的因果推論を学んでいると、因果関係は捉えたけども、そのモデルにて予測を行ってみたいと思うことがありました。因果推論と予測は別物なので、得られたデータを検討する際には注意しなければいけません。因果関係を明らかにするということは、原因となる要因が結果となる要因にどのような影響を及ぼしているかを明らかにすることにつながります。
　例えば、ある薬を飲んで病気の症状が緩和するということが分かれば、薬を飲むという行為によって病気の治癒につながるという因果関係が存在することが認識できます。加えて、ある薬を飲むと健康に関わる数値が変化するということが分かったとします。もっと詳しく掘り下げてみます。ある薬を1回飲むと健康に関わる数値が10減少するということが分かったとします。この数値の減少は症状の緩和を示す指標の一つだとすると、薬と病気との因果関係には、薬を飲むことによって症状を緩和させる影響(健康に関わる数値が10減少すること)が存在していることが判明します。
　ここで視点を変えてみます。薬を飲むことによってどのくらい健康に関わるデータが減少するのかという立場に立つとします。そうすると、この薬を飲むことで健康に関わる数値がどれくらい減少するのかと考えることになり、このデータから得られる視点は予測になります。因果の視点でデータを捉えるか、予測の視点でデータを捉えるかで、データが持つ意味が変わってきます。
　多くの人にとっては、因果と予測は別物で相いれない関係だと捉えてしまうかもしれません。ですが、統計素人である自分にとってはとある疑問が浮かんできました。まずは因果の視点から立って因果関係を把握して、その因果関係のモデルから予測を立てることはできないだろうか。イメージとしては↓の図のような感じです。


図1 疑問

　この疑問に一つの光を差しのべてくれたのがベイジアンネットワークでした。

2. DAG(Directed Acyclic Graph)

　ベイジアンネットワークの話に移る前に、押さえておくべき用語があります。それが有向非循環グラフ(通称DAG)という用語です。因果推論の際には、変数から他の変数に関連を示す場合には、グラフィカルモデルというもの使って表現します。これは、変数間を矢印で結ぶことによって因果の流れを視覚的に捉えることができるグラフです。例えば下の図を見てください。
　

図2 因果の流れ

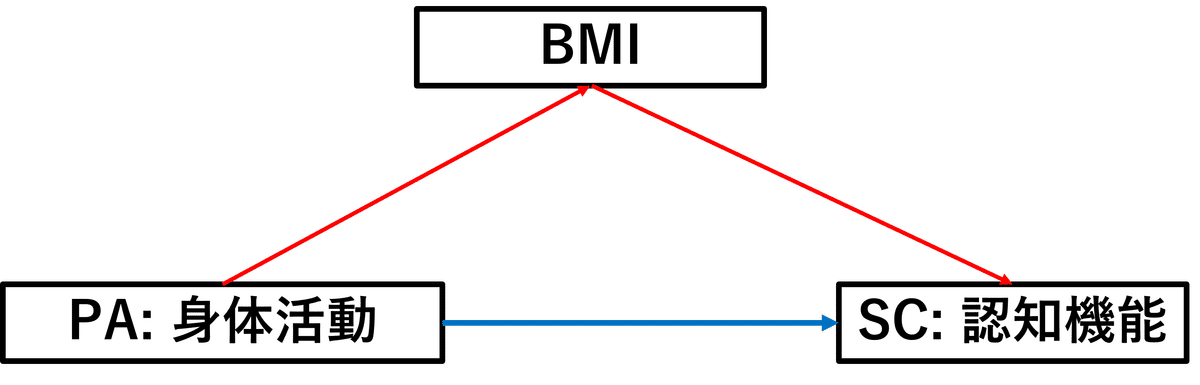
　↑図では、身体活動・BMI・認知機能(認知パフォーマンス)という関係がグラフィカルモデルによって表現されています。この図から、身体活動は認知機能に影響を与えており、かつBMIにも影響を与えているととが分かります。加えて、身体活動から影響を受けたBMIは認知機能に影響を与えていることも分かります。このモデルのように、矢印を辿っても元の変数に帰ってこないことを非循環と言います。また、矢印の向きが示されていることを有向と言います。この非循環と有向が合わさったグラフィカルモデルを有向非循環グラフと言います。英語では、Directed Acyclic Graphというので、略されてDAGと呼ばれています。

図2に示した因果関係の図は架空のモデルなので実際の現象とは異なることがありますのでご注意ください。

3. ベイジアンネットワーク

　ベイジアンネットワークでは、第2章にて述べたDAGの概念を用いて、パラメータ推定ということを行っていきます。例えば下の図のような因果関係が分かったとします。


図3 ベイジアンネットワークに用いるDAG

　図3では、身体活動がBMIに影響が与えられて、影響を与えられたBMIが認知機能に影響を与えています。ベイジアンネットワーク用いることによって、身体活動からBMIに向かうパラメータやBMIから認知機能に向かうパラメータの推定を行うことができます。つまり、パラメータ推定をすることで、身体活動の変数・BMIの変数・認知機能の変数を予測することができます。今回は連続型のデータにて、多変量正規(ガウス)分布を用いた因果モデルにおけるパラメータ推定を行っていきます。このような確率分布を用いてデータを予測するというプロセスは、ベイズ統計モデリングと似ている点がありますね。

　正規分布によるパラメータ推定ということなので、ベイジアンネットワークにおけるパラメータ推定を図にすると↓図のようになります。

図4 パラメータの表現

　Normalというのが正規分布を示しています。ということで、正規分布に即したパラメータを推定していることが分かります。このパラメータを用いることで変数の予測を行うことできます。つまり、このパラメータによって、PA・BMI・SCのどの変数でも予測することが可能になります。

4. Rによる実装

　ベイジアンネットワークでできることが分かったので、最後にRを用いてベイジアンネットワークを実装してみることで理解を深めていきます。詳しいコードの説明については、参考文献・資料の[5]・[6]・[7]・[8]をご参照ください。
4.1 データセット作成
　データセットは乱数発生によって作成した疑似データを用います。データセットは↓のコードを用いて作成しました。データの総数は1500としています。

set.seed(1234)
ta=rnorm(500,60,5) #正規分布：平均60で標準偏差5の乱数
tb=rnorm(500,70,5) #正規分布：平均70で標準偏差5の乱数
tc=rnorm(500,80,5) #正規分布：平均80で標準偏差5の乱数
#身体活動量の乱数生成
ea=rnorm(500,20,5) #正規分布：平均20で標準偏差5の乱数
eb=rnorm(500,40,5) #正規分布：平均40で標準偏差5の乱数
ec=rnorm(500,60,5) #正規分布：平均60で標準偏差5の乱数
#BMIの乱数生成
ra=rnorm(500,40,2) #正規分布：平均40で標準偏差2の乱数
rb=rnorm(500,30,2) #正規分布：平均30で標準偏差2の乱数
rc=rnorm(500,20,2) #正規分布：平均20で標準偏差2の乱数
#データフレームの作成
data1=data.frame(ta,ea,ra)　
data2=data.frame(tb,eb,rb)
data3=data.frame(tc,ec,rc)
#データフレームの列名変更
names(data1) <- c("SC", "PA","BMI")
names(data2) <- c("SC", "PA","BMI")
names(data3) <- c("SC", "PA","BMI")
#データフレームの結合
data12=rbind(data1,data2)
data_all=rbind(data12,data3)

4.2 必要なパッケージのインポート
　今回のベイジアンネットワークの実装で必要なパッケージをインポートします。bnlearnというパッケージがベイジアンネットワークを行うために使用するパッケージとなっています。

library(dplyr)
library(bnlearn)
library(igraph)
library(forecast)
library(ggplot2)

4.3 DAGの作成
　次に判明している因果モデルのDAGを作成します。

dag.bnlearn = model2network("[PA][BMI|PA][SC|BMI]")
dag.igraph = as.igraph(dag.bnlearn)
ly=matrix(c(1,1,2,2,1,2),3)
vcol=c( "darkgray", "darkgray","black")
plot(dag.igraph, layout=ly,vertex.size=50, edge.arrow.size=1,
     edge.color="black", vertex.color=vcol, vertex.label.color="white")

このコードを実行すると↓図が作成出来て、意図したDAGが作成できていることを確認できます。

図5 DAG

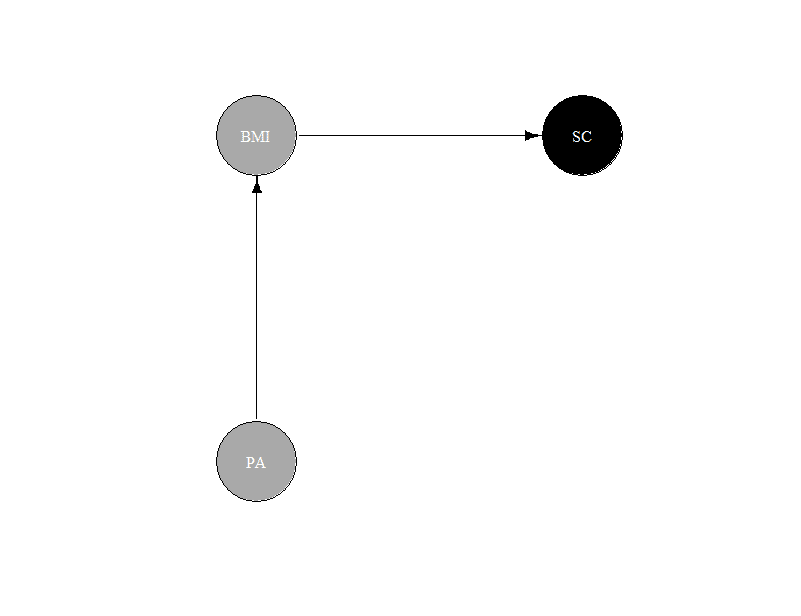
　図4の図と配置が違いますが、表していることは同じです。dag.bnlearn = model2network("[PA][BMI|PA][SC|BMI]")というコードでDAGを作成しています。作成したDAGをigraphパッケージを用いて図5のように図示しています。

4.3 パラメーター推定
　作成したDAGから多変正規分布を用いたベイジアンネットワークによるパラメーター推定を行います。

fit=bn.fit(dag.bnlearn, data_all)

　パラメーターの推定がたった1行でできるとは凄すぎますね、結果を↓に示します。

図6 パラメーター推定の結果

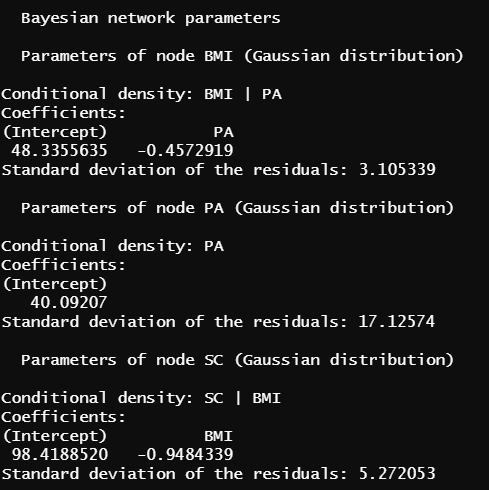
　図6で得られた結果を、正規分布の表記で示した図が↓になります。

図7 正規分布によるパラメーター推定の表示

　得られらパラメーターが正規分布に沿っているかどうかQ-Qplotとヒストグラムを作成して確認してみます。

#QQplotの作成
bn.fit.qqplot(fit)


図8 Q-Qplot

図8のQ-Qplotを見てみると、PAの分布がちょっとおかしいですね。。。まあ、乱数発生で作った疑似データなので仕方がないのかもしれません。。。
ヒストグラムでも確認してみます。

#ヒストグラム
bn.fit.histogram(fit)


図9 ヒストグラム

といった感じになりました。

4.4 データの予測
　ここまででベイジアンネットワークを用いたパラメータ推定が実装できました。この流れを用いて、全データを訓練データ(全データの70%)とテストデータ(全データの30%)に分けます。訓練データでパラメータ推定をしてテストデータに当てはめてみて、どれくらいの精度で推定できるか確認していきます。この流れは、一般出来な機械学習と同じですね。今回は、認知機能(SC)の予測を行っていきます。
　4.4.1 訓練データとテストデータの振り分け

#訓練データとテストデータの振り分け
set.seed(123)
data_all.rows = nrow(data_all) # 1500
train.rate = 0.7 # 訓練データの比率
train.index <- sample(data_all.rows, data_all.rows * train.rate)
training.set = data_all[train.index,] # 訓練データ
test.set = data_all[-train.index,] # テストデータ

　4.4.2 訓練データを用いたパラメータ推定

fitted = bn.fit(dag.bnlearn, training.set) #訓練データを用いたパラメータの学習

　fittedに格納したパラメータ推定の結果を↓に示します。

Bayesian network parameters

  Parameters of node BMI (Gaussian distribution)

Conditional density: BMI | PA
Coefficients:
(Intercept)           PA  
 48.3479243   -0.4579977  
Standard deviation of the residuals: 3.170778 

  Parameters of node PA (Gaussian distribution)

Conditional density: PA
Coefficients:
(Intercept)  
   40.46892  
Standard deviation of the residuals: 16.92962 

  Parameters of node SC (Gaussian distribution)

Conditional density: SC | BMI
Coefficients:
(Intercept)          BMI  
 98.9204921   -0.9651268  
Standard deviation of the residuals: 5.226312

　この結果をDAGにおいて正規分布にて表現します(↓図)

図11 訓練データを用いたパラメータ推定

　4.4.3 テストデータによるデータの予測とその精度

pred = predict(fitted, "SC", method="bayes-lw", test.set) #SCの予測
head(cbind(pred,test.set[, "SC"]))  
accuracy(pred, test.set[, "SC"]) #正確度の算出
> accuracy(pred, test.set[, "SC"]) #正確度の算出
                 ME     RMSE      MAE        MPE     MAPE
Test set 0.01203314 5.395869 4.323941 -0.5396051 6.407836

　精度の確認では、二乗平均平方根誤差(RMSE: Root Mean Square Error)が5.396となりました。この値は小さいほどより精度が高いことを示しています。
　予測したデータ(X軸)とテストデータ(Y軸)を図にしてどれくらい予測が出来てていたか確認してみます。

df = data.frame(prediction=pred,actual=test.set[, "SC"])
p = ggplot(df,aes(x = prediction,y = actual)) + geom_point(size=5,color = "red",alpha = 0.4) +theme_bw() + theme(text = element_text(size = 24))
p = p+xlim(c(50, 100))+ylim(c(40, 100))
p = p+xlab("予測値")+ylab("テストデータセット")
p = p+stat_smooth(method = "lm", se = TRUE, size = 1)
plot(p)
図12 予測したデータ(X軸)とテストデータ(Y軸)

 　ある程度は予測できていたのではないでしょうか。ただまだまだ改善の余地がありありですね。
　最後に予測値(X軸)と残差(Y軸)の図から精度を確認してみます。

p = ggplot(df,aes(pred,pred - test.set[, "SC"])) + geom_point(size=5,color = "red",alpha = 0.4) +theme_bw() + theme(text = element_text(size = 24))
p = p+xlab("予測値")+ylab("残差")
p = ggplot(df,aes(pred,pred - test.set[, "SC"])) + geom_point(size=5,color = "red",alpha = 0.4) +theme_bw() + theme(text = element_text(size = 24))
p = p+xlab("予測値")+ylab("残差")
p = p+xlim(c(40, 100))+ylim(c(-20, 20))
p = p + geom_hline(yintercept = 0,
                   colour = "blue", # 色
                   size = 2, # 線の太さ
                   alpha = 0.5, # 透明度
                   linetype = 2) # 線の種類
p


図13 予測したデータ(X軸)と残差(Y軸)

　図13では、青の点線で示した残差0の付近にデータがあれば予測したデータとテストデータとの差が小さいことを示しており、精度が良いことを確認する指標になります。残念ながら残差が大きいデータが多くあるので精度が良いとはお世辞にも言えないようです。

5. おわりに

　最後まで読んでいただき誠にありがとうございました。noteの記事については、自分が学習したことのアウトプットとして活用しています。今回はベイジアンネットワークについてRでの実装を試みました。実際に実装してみるとこで、ベイジアンネットワークによる予測を体感することができました。まだまだ知識不足や理解不足のため、本記事において説明が分かりづらい点があったと思います。その際にはぜひ遠慮せずにご質問していただければと思います。また、説明やコードの改善点・間違いがありましたらご指摘していただけると非常にありがたいです。引き続き統計の勉強に邁進していきます。この記事を読んで、「勉強頑張れ！」と思った方がいましたら、今後のモチベーションにつながりますので、ぜひ「いいね」を押していただけると非常にありがたいです。

参考文献・資料

  1. Judea Pearl (著), Madelyn Glymour (著), Nicholas P. Jewell (著), 落海 浩 (翻訳), 2019年, 入門 統計的因果推論, 朝倉書店

  2. 清水昌平, 2017年, 統計的因果探索 (機械学習プロフェッショナルシリーズ)　講談社

  3. 黒木学, 2017年, 構造的因果モデルの基礎, 共立出版

  4. 鈴木 譲 (著, 編集), 植野 真臣 (著, 編集), 2016年, 確率的グラフィカルモデル, 共立出版

  5. Marco Scutari (著), Jean-Baptiste Denis (著), 金 明哲 (監修), 財津 亘 (翻訳), 2022年, Rと事例で学ぶベイジアンネットワーク〔原著第2版〕, 共立出版

  6. Predict or impute missing data from a Bayesian network

  7. かものはしの分析ブログ ベイジアンネットワークをRのbnlearnパッケージで推定して予測してみる

  8. 統計コンサルの議事メモ ベイジアンネットワークで変数間の関連性を見る

  9. 線形単回帰・重回帰分析に基づき予測モデルを作成｜機械学習・Pythonによるscikit-learnモデル開発・評価

  10. もものきとデータ解析をはじめよう Rでデータ解析を始めよう005 Rで機械学習（SVMでIris分類）

  11. Judea Pearl (著), Dana Mackenzie (著), 2019年, The Book of Why: The New Science of Cause and Effect, Penguin

  12. ジューディア・パール (著), ダナ・マッケンジー (著), 松尾 豊 (解説), 夏目 大 (翻訳), 2022年, 因果推論の科学 「なぜ?」の問いにどう答えるか, 文藝春秋, (参考文献・資料[11]の和訳版)

注意：本記事では乱数発生によってデータセットを作成しています。そのため、本記事での結果が一般的な現象の結果を表しているわけではございませんのでご注意ください。