
筋力強化のためのトレーニングメニュー提示プログラム
筋力強化に特化したトレーニングプログラムを提示してくれるコード(pythonにて)を作成しました.強化するトレーニングは,スクワット・ベンチプレス・デッドリフトの3種目となっています.
このトレーングメニューは,day1~day4の4回のトレーニングを1つのweekの単位とするマイクロサイクルになっています.トレーング内容は,スクワット週2回,ベンチプレス週2回,デッドリフト週1回としています.
流れとしては,個人データの入力→推定ベスト重量の算出→疲労度とトレーニング強度の感想→トレーニングメニューの提示となっています.
推定ベスト重量は,2019年に開催されたジャパンクラシックパワーリフティング選手権大会(JCP)の男子のデータで重回帰の予測モデルから算出します.
トレーニングプログラムは,ピリオダイゼーションにも適用できるように,adaptation or deload期間,Strehngth development期間,Maximum muscle strength期間の3つの期間を選べるようになっています.Adaptation or deload期間では運動強度60%で8レップ2セットを中心に,Strehngth development期間では運動強度75%で5レップ4セットを中心に,Maximum muscle strength期間では運動強度87.5%で2レップ3セットを中心にしています.
プログラムのコードは↓からダウンロードできるようになっています.
コード全体は,この記事の一番最後に載せています.
コードの解説をしていきます.
1. 個人データの入力
#個人データ入力
#体重
weight=100
#年齢
age=20
#試合の日の第一試技にする重量 or マックス重量の90%~95%の重量
SQs1=200 #スクワット(SQ)
BNs1=100 #ベンチプレス(BN)
DLs1=200 #デッドリフト(DL)体重(kg)と年齢(歳)の数値をまず入力します.そのあとに,パワーリフティングの試合日における第一試技の重量を入力します.もし第一試技にする重量が分からない人は,マックス重量の90%~95%の重量を入力してください(ここでは,試合日の第一試技にする重量をマックス重量の90%~95%の重量だと仮定しています).今回は,仮のデータとして,体重に100,年齢に20,試合の日の第一試技にする重量のスクワットを200,試合の日の第一試技にする重量のベンチプレスを100,試合の日の第一試技にする重量のデッドリフトを200と入力しています.
2. 推定ベスト重量の算出
#推定ベスト重量の算出
#SQの推定ベスト重量
SQm=SQs1*0.982917+weight*0.157134+age*(-0.049384)+6.9212514881147
SQ=SQm
print('SQの推定ベスト重量:{}kg'.format(round(SQm)))
#BNの推定ベスト重量
BNm=BNs1*1.017229+weight*0.031749+age*(-0.055048)+4.97202673216031
BN=BNm
print('BNの推定ベスト重量:{}kg'.format(round(BNm)))
#DLの推定ベスト重量
DLm=DLs1*0.943229+weight*0.140076+age*(-0.077887)+17.6758487040875
DL=DLm
print('DLの推定ベスト重量:{}kg'.format(round(DLm)))この式で,ベスト重量を推定しています.この式は,
日本パワーリフティング協会 2019年02月09日(土)-11日(月・祝) 第23回ジャパンクラシックパワーリフティング選手権大会
https://www.jpa-powerlifting.or.jp/japan_new/japan_2018
のデータをもとに重回帰の予測モデルをつくり,機械学習によってベスト重量を推定しています.
この式を適応すると,↓の結果が得られます.

3. トレーニングに関する情報を入力
#トレーニングに関する情報を入力
#トレーニング週
week=2
#トレーニングメニュー(1:adaptation or deload, 2:Strehngth development, 3: Maximum muscle strength)
m=2
#疲労
#疲労の度合いを1~10のスケールで(1が疲れていない10が疲れている)
f=2
#強度
#先週のトレーニングはきつかった(0:イージー, 1:まあまあ, 2:ハード)
t=2ここでは,トレーニングに関する情報を入力します.トレーニング週がいつなのか入力します.トレーニングの目的を,1:adaptation or deload, 2:Strehngth development, 3: Maximum muscle strengthから選びます.現在の疲労度を1~10のスケールで(1が疲れていない10が疲れている)入力します.先週のトレーニングはきつかったかどうかについて,0:イージー, 1:まあまあ, 2:ハードで入力します.例えとして今回は,week2として,Strehngth developmentを目的にします.疲労度は,あまり疲れていないとして2として入力してます.先週のトレーニング強度は,まあまあきつかったの2として入力してます.
疲労度が0~3の時にはレップ数とセット数を1回ずつ増やして,疲労度が8以上の時にはレップ数とセット数を1回ずつ減らしています.疲労度が5~7の時にはレップ数とセット数は変わりません.疲労度からレップ数とセット数を変更することで,総負荷量が変わりようになっています.
先週のトレーニングはきつかったかどうかについて,0の「イージー」と答えた場合には運動強度を5%高くなるようにして,, 2の「ハード」と答えた場合には運動強度を5%低くなるようにしています. 1の「まあまあ」と答えた場合には運動強度は変更されません.先週のトレーニングはきつさによって,運動強度が変わるようになっています.
4. トレーニングメニューの提示
#トレーニングメニューの提示
print('week'+str(week))
#基本情報
#_____________________________________________________________________________________________________
#adaptation or deload
if m==1:
if 0< f < 4:
r=8+1 #レップ数
s=2+1 #セット数
elif 5< f < 7:
r=8 #レップ数
s=2 #セット数
else:
r=8-1 #レップ数
s=2-1 #セット数
if t==0:
ins=0.6+0.05 #運動強度
elif t==1:
ins=0.6 #運動強度
else:
ins=0.6-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
#_____________________________________________________________________________________________________
#Strehngth development
elif m==2:
if 0< f < 4:
r=5+1 #レップ数
s=4+1 #セット数
elif 5< f < 7:
r=5 #レップ数
s=4 #セット数
else:
r=5-1 #レップ数
s=4-1 #セット数
if t==0:
ins=0.75+0.05 #運動強度
elif t==1:
ins=0.75 #運動強度
else:
ins=0.75-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
#_____________________________________________________________________________________________________
#Maximum muscle strength
else:
if 0< f < 4:
r=2+1 #レップ数
s=3+1 #セット数
elif 5< f < 7:
r=2 #レップ数
s=3 #セット数
else:
r=2-1 #レップ数
s=3-1 #セット数
if t==0:
ins=0.875+0.05 #運動強度
elif t==1:
ins=0.875 #運動強度
else:
ins=0.875-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))ここでは,入力する数値はありません.Shift+Enterを押してコードを実行するだけです.コードを実行することで,これまで入力した情報からトレーニングメニューが自動的に提示されます.今回入力したデータだと↓のアウトプットが得られます.

week2のトレーニングの内訳は,
day1にスクワット153kgを6レップ5セット,ベンチプレス76kgを6レップ6セット.
day2にはデッドリフト153kg153kgを6レップ5セット,ポーズドデッドリフト109kgを4レップ4セット.
day3には,スクワット153kgを6レップ5セット,ポーズドスクワット109kgを4レップ4セット.
day4には,ベンチプレス76kgを6レップ7セット,ナローベンチプレス54kgを6レップ6セット.
となっています.
上記のコードを説明した解説動画をYoutubeにアップしました.この動画を見ていただくと,このコードを具体的にどのように使うのか理解できると思います.
今回作成したトレーニング提示プログラムが,トレーニング計画作成のお役に立てれれば嬉しいです.
コード全体は↓になっています.
#個人データ入力
#体重
weight=100
#年齢
age=20
#試合の日の第一試技にする重量 or マックス重量の90%~95%の重量
SQs1=200 #スクワット(SQ)
BNs1=100 #ベンチプレス(BN)
DLs1=200 #デッドリフト(DL)
#推定ベスト重量の算出
#SQの推定ベスト重量
SQm=SQs1*0.982917+weight*0.157134+age*(-0.049384)+6.9212514881147
SQ=SQm
print('SQの推定ベスト重量:{}kg'.format(round(SQm)))
#BNの推定ベスト重量
BNm=BNs1*1.017229+weight*0.031749+age*(-0.055048)+4.97202673216031
BN=BNm
print('BNの推定ベスト重量:{}kg'.format(round(BNm)))
#DLの推定ベスト重量
DLm=DLs1*0.943229+weight*0.140076+age*(-0.077887)+17.6758487040875
DL=DLm
print('DLの推定ベスト重量:{}kg'.format(round(DLm)))
#トレーニングに関する情報を入力
#トレーニング週
week=2
#トレーニングメニュー(1:adaptation or deload, 2:Strehngth development, 3: Maximum muscle strength)
m=2
#疲労
#疲労の度合いを1~10のスケールで(1が疲れていない10が疲れている)
f=2
#強度
#先週のトレーニングはきつかった(0:イージー, 1:まあまあ, 2:ハード)
t=2
#トレーニングメニューの提示
print('week'+str(week))
#基本情報
#_____________________________________________________________________________________________________
#adaptation or deload
if m==1:
if 0< f < 4:
r=8+1 #レップ数
s=2+1 #セット数
elif 5< f < 7:
r=8 #レップ数
s=2 #セット数
else:
r=8-1 #レップ数
s=2-1 #セット数
if t==0:
ins=0.6+0.05 #運動強度
elif t==1:
ins=0.6 #運動強度
else:
ins=0.6-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
#_____________________________________________________________________________________________________
#Strehngth development
elif m==2:
if 0< f < 4:
r=5+1 #レップ数
s=4+1 #セット数
elif 5< f < 7:
r=5 #レップ数
s=4 #セット数
else:
r=5-1 #レップ数
s=4-1 #セット数
if t==0:
ins=0.75+0.05 #運動強度
elif t==1:
ins=0.75 #運動強度
else:
ins=0.75-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
#_____________________________________________________________________________________________________
#Maximum muscle strength
else:
if 0< f < 4:
r=2+1 #レップ数
s=3+1 #セット数
elif 5< f < 7:
r=2 #レップ数
s=3 #セット数
else:
r=2-1 #レップ数
s=3-1 #セット数
if t==0:
ins=0.875+0.05 #運動強度
elif t==1:
ins=0.875 #運動強度
else:
ins=0.875-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))まず第一号のプロトタイプとしてトレーニングメニューのプログラミングコードを作成しました.今後,さらに改良を加えていきたいと考えています.ご指摘や要望等がございましたら,ぜひ教えていただきたいです.今回作成したコードに反映させていただきます.
__________________________________
*1 追加で,総負荷量が自動的に算出されるコードを追加しました.例として↓のように提示されます.

追加したコードのファイルは↓からダウンロードできます.
トレーニングメニューの提示の箇所での追加は↓のようになっています.
#トレーニングメニューの提示
print('week'+str(week))
#基本情報
#_____________________________________________________________________________________________________
#adaptation or deload
if m==1:
if 0< f < 4:
r=8+1 #レップ数
s=2+1 #セット数
elif 5< f < 7:
r=8 #レップ数
s=2 #セット数
else:
r=8-1 #レップ数
s=2-1 #セット数
if t==0:
ins=0.6+0.05 #運動強度
elif t==1:
ins=0.6 #運動強度
else:
ins=0.6-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
SQd1t=SQd1*SQr1*SQs1 #総負荷量
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
BNd1t=BNd1*BNr1*BNs1 #総負荷量
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
print('スクワットの総負荷量:{}kg, ベンチプレスの総負荷量:{}kg'.format(SQd1t,BNd1t))
print('_________________________________________________________________')
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
DLd1t=DLd1*DLr1*DLs1 #総負荷量
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
PDLd1t=PDLd1*PDLr1*PDLs1 #総負荷量
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
print('デッドリフトの総負荷量:{}kg, Pausedデッドリフトの総負荷量:{}kg'.format(DLd1t,PDLd1t))
print('_________________________________________________________________')
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
SQd1_2t=SQd1_2*SQr1_2*SQs1_2 #総負荷量
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
PSQd1_2t=PSQd1_2*PSQr1_2*PSQs1_2 #総負荷量
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
print('スクワットの総負荷量:{}kg, Pausedスクワットの総負荷量:{}kg'.format(SQd1_2t,PSQd1_2t))
print('_________________________________________________________________')
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
BNd1_2t=BNd1_2*BNr1_2*BNs1_2 #総負荷量
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
NBNd1_2t=NBNd1_2*NBNr1_2*NBNs1_2 #総負荷量
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
print('ベンチプレスの総負荷量:{}kg, ナローベンチプレスの総負荷量:{}kg'.format(BNd1_2t,NBNd1_2t))
print('_________________________________________________________________')
#_____________________________________________________________________________________________________
#Strehngth development
elif m==2:
if 0< f < 4:
r=5+1 #レップ数
s=4+1 #セット数
elif 5< f < 7:
r=5 #レップ数
s=4 #セット数
else:
r=5-1 #レップ数
s=4-1 #セット数
if t==0:
ins=0.75+0.05 #運動強度
elif t==1:
ins=0.75 #運動強度
else:
ins=0.75-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
SQd1t=SQd1*SQr1*SQs1 #総負荷量
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
BNd1t=BNd1*BNr1*BNs1 #総負荷量
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
print('スクワットの総負荷量:{}kg, ベンチプレスの総負荷量:{}kg'.format(SQd1t,BNd1t))
print('_________________________________________________________________')
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
DLd1t=DLd1*DLr1*DLs1 #総負荷量
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
PDLd1t=PDLd1*PDLr1*PDLs1 #総負荷量
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
print('デッドリフトの総負荷量:{}kg, Pausedデッドリフトの総負荷量:{}kg'.format(DLd1t,PDLd1t))
print('_________________________________________________________________')
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
SQd1_2t=SQd1_2*SQr1_2*SQs1_2 #総負荷量
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
PSQd1_2t=PSQd1_2*PSQr1_2*PSQs1_2 #総負荷量
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
print('スクワットの総負荷量:{}kg, Pausedスクワットの総負荷量:{}kg'.format(SQd1_2t,PSQd1_2t))
print('_________________________________________________________________')
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
BNd1_2t=BNd1_2*BNr1_2*BNs1_2 #総負荷量
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
NBNd1_2t=NBNd1_2*NBNr1_2*NBNs1_2 #総負荷量
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
print('ベンチプレスの総負荷量:{}kg, ナローベンチプレスの総負荷量:{}kg'.format(BNd1_2t,NBNd1_2t))
print('_________________________________________________________________')
#_____________________________________________________________________________________________________
#Maximum muscle strength
else:
if 0< f < 4:
r=2+1 #レップ数
s=3+1 #セット数
elif 5< f < 7:
r=2 #レップ数
s=3 #セット数
else:
r=2-1 #レップ数
s=3-1 #セット数
if t==0:
ins=0.875+0.05 #運動強度
elif t==1:
ins=0.875 #運動強度
else:
ins=0.875-0.05 #運動強度
#day1
SQd1=round(SQ*ins)
SQr1=r
SQs1=s
SQd1t=SQd1*SQr1*SQs1 #総負荷量
BNd1=round(BN*ins)
BNr1=r
BNs1=s+1
BNd1t=BNd1*BNr1*BNs1 #総負荷量
print('day1')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1,SQr1,SQs1))
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1,BNr1,BNs1))
print('スクワットの総負荷量:{}kg, ベンチプレスの総負荷量:{}kg'.format(SQd1t,BNd1t))
print('_________________________________________________________________')
#day2
DLd1=round(DL*ins)
DLr1=r
DLs1=s
DLd1t=DLd1*DLr1*DLs1 #総負荷量
PDLd1=round(DL*(ins-0.2))
PDLr1=r-2
PDLs1=s-1
PDLd1t=PDLd1*PDLr1*PDLs1 #総負荷量
print('day2')
print('DL:{}kg×Reps:{}×Sets:{}'.format(DLd1,DLr1,DLs1))
print('Paused DL:{}kg×Reps:{}×Sets:{}'.format(PDLd1,PDLr1,PDLs1))
print('デッドリフトの総負荷量:{}kg, Pausedデッドリフトの総負荷量:{}kg'.format(DLd1t,PDLd1t))
print('_________________________________________________________________')
#day3
SQd1_2=round(SQ*ins)
SQr1_2=r
SQs1_2=s
SQd1_2t=SQd1_2*SQr1_2*SQs1_2 #総負荷量
PSQd1_2=round(SQ*(ins-0.2))
PSQr1_2=r-2
PSQs1_2=s-1
PSQd1_2t=PSQd1_2*PSQr1_2*PSQs1_2 #総負荷量
print('day3')
print('SQ:{}kg×Reps:{}×Sets:{}'.format(SQd1_2,SQr1_2,SQs1_2))
print('Paused SQ:{}kg×Reps:{}×Sets:{}'.format(PSQd1_2,PSQr1_2,PSQs1_2))
print('スクワットの総負荷量:{}kg, Pausedスクワットの総負荷量:{}kg'.format(SQd1_2t,PSQd1_2t))
print('_________________________________________________________________')
#day4
BNd1_2=round(BN*ins)
BNr1_2=r
BNs1_2=s+2
BNd1_2t=BNd1_2*BNr1_2*BNs1_2 #総負荷量
NBNd1_2=round(BN*(ins-0.2))
NBNr1_2=r
NBNs1_2=s+2
NBNd1_2t=NBNd1_2*NBNr1_2*NBNs1_2 #総負荷量
print('day4')
print('BN:{}kg×Reps:{}×Sets:{}'.format(BNd1_2,BNr1_2,BNs1_2))
print('Narrow BN:{}kg×Reps:{}×Sets:{}'.format(NBNd1_2,NBNr1_2,NBNs1_2))
print('ベンチプレスの総負荷量:{}kg, ナローベンチプレスの総負荷量:{}kg'.format(BNd1_2t,NBNd1_2t))
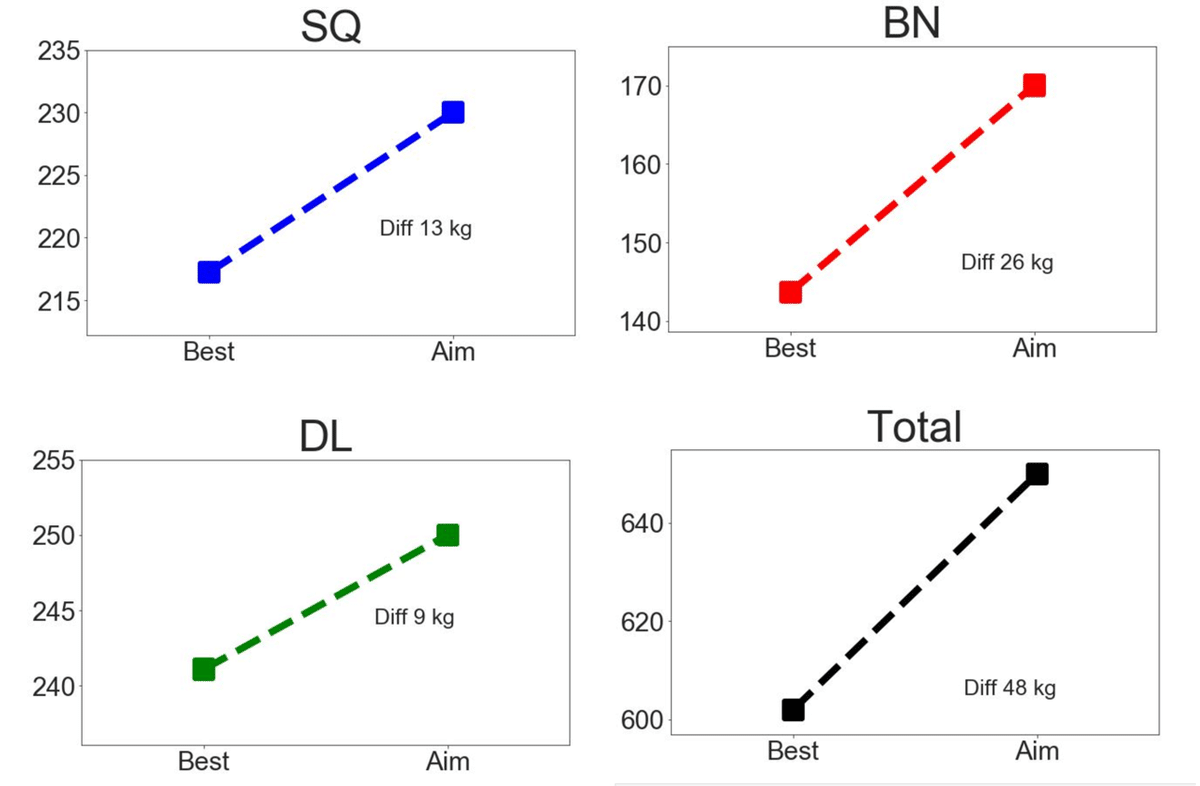
print('_________________________________________________________________')*2 追加で,現在の推定ベスト重量と目標重量との差を示すグラフを示すコードを付け足しました.目標達成に向けてモチベーションを高めるのが狙いです.Bestが現在の推定ベスト重量を示し,Aimが目標重量を示しています.グラフ中に表示されるdiffは,目標重量と推定ベスト重量の差を表しています.
ファイルは↓からダウンロードできます.
追加したコードは↓のようになっています.
#スクワット(SQ),ベンチプレス(BN),デッドリフト(DL)の目標値
SQaim=230
BNaim=170
DLaim=250
#図の描写
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')#グラフの背景を白くする
%matplotlib inline
array_SQ={'Best': [SQ], 'Aim': [SQaim]}
df_SQ= pd.DataFrame.from_dict(array_SQ)
array_BN={'Best': [BN], 'Aim': [BNaim]}
df_BN= pd.DataFrame.from_dict(array_BN)
array_DL={'Best': [DL], 'Aim': [DLaim]}
df_DL= pd.DataFrame.from_dict(array_DL)
#SQ
plt.figure(figsize=(10,6))
sns.set_style('ticks')#grid線を消す
sns.pointplot( data=df_SQ,color="Blue", linestyles=["--"], scale=3.0,errwidth=5.0,markers="s")
plt.tick_params(labelsize = 30)
plt.title("SQ", size=50)
plt.ylabel("", size=50)
plt.xlabel("")
plt.text(0.7,SQ+3,'Diff '+str(round(SQaim-SQ))+' kg', size=25)
plt.ylim(SQ-5, SQaim+5)#y軸の範囲
#BN
plt.figure(figsize=(10,6))
sns.set_style('ticks')#grid線を消す
sns.pointplot( data=df_BN,color="Red", linestyles=["--"], scale=3.0,errwidth=5.0,markers="s")
plt.tick_params(labelsize = 30)
plt.title("BN", size=50)
plt.ylabel("", size=50)
plt.xlabel("")
plt.text(0.7,BN+3,'Diff '+str(round(BNaim- BN))+' kg', size=25)
plt.ylim(BN-5, BNaim+5)#y軸の範囲
#DL
plt.figure(figsize=(10,6))
sns.set_style('ticks')#grid線を消す
sns.pointplot( data=df_DL,color="Green", linestyles=["--"], scale=3.0,errwidth=5.0,markers="s")
plt.tick_params(labelsize = 30)
plt.title("DL", size=50)
plt.ylabel("", size=50)
plt.xlabel("")
plt.text(0.7,DL+3,'Diff '+str(round(DLaim-DL))+' kg', size=25)
plt.ylim(DL-5, DLaim+5)#y軸の範囲
#Total
TO=SQ+BN+DL
TOaim=SQaim+BNaim+DLaim
array_TO={'Best': [TO], 'Aim': [TOaim]}
df_TO= pd.DataFrame.from_dict(array_TO)
plt.figure(figsize=(10,6))
sns.set_style('ticks')#grid線を消す
sns.pointplot( data=df_TO,color="Black", linestyles=["--"], scale=3.0,errwidth=5.0,markers="s")
plt.tick_params(labelsize = 30)
plt.title("Total", size=50)
plt.ylabel("", size=50)
plt.xlabel("")
plt.text(0.7,TO+3,'Diff '+str(round(TOaim-TO))+' kg', size=25)
plt.ylim(TO-5, TOaim+5)#y軸の範囲参考資料
1. TSA 9 Week Intermediate Powerlifting Program (v1.0 + v2.0)
https://liftvault.com/programs/powerlifting/tsa-9-week-intermediate-program/
2. パワーズ運動生理学 体力と競技力向上のための理論と応用
3. Periodization Training for Sports
4. Science and Practice of Strength Training
5. Peterson, M. D., Rhea, M. R., & Alvar, B. A. (2004). Maximizing strength development in athletes: a meta-analysis to determine the dose-response relationship. The Journal of Strength & Conditioning Research, 18(2), 377-382.
6. Rhea, M. R., Alvar, B. A., Burkett, L. N., & Ball, S. D. (2003). A meta-analysis to determine the dose response for strength development.
