Cinderellaで数学:いろいろな曲線:カバリエリの円錐曲線作図器
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されているカバリエリの円錐曲線(放物線・楕円・双曲線)の作図器です。
放物線
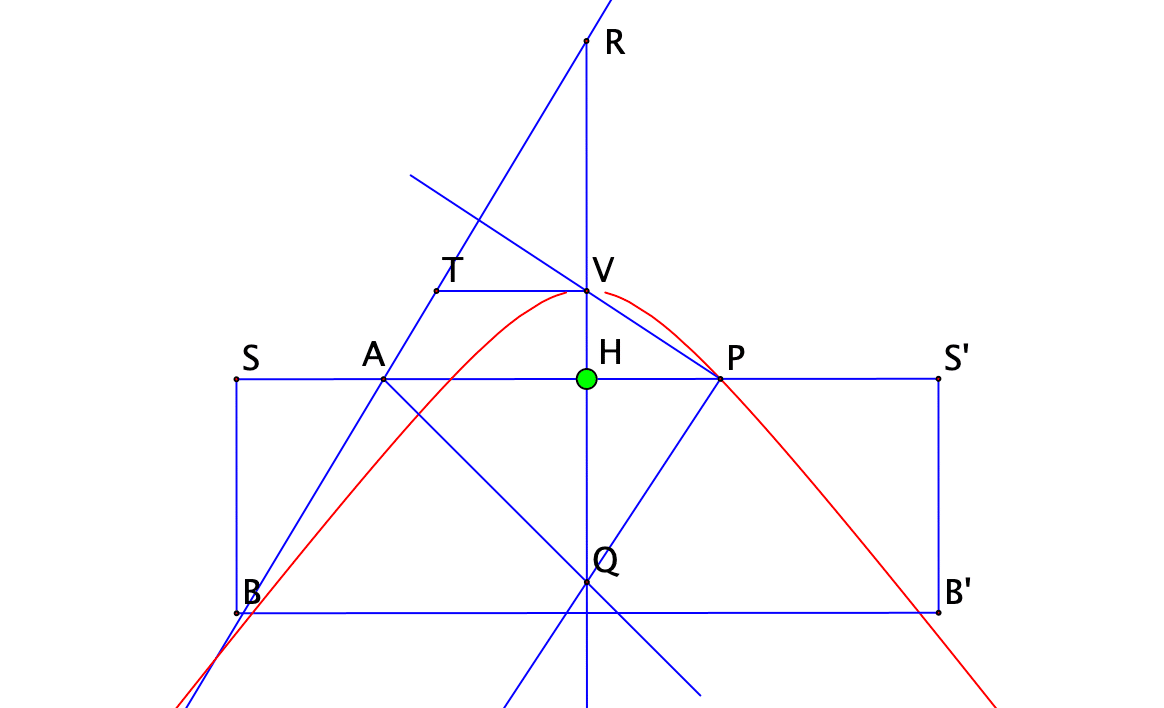
図にある長方形 SBB'S'は,直線VQに沿って縦方向に滑り動くことができる。点Hは線分 SS' の中点を表している。点Qは,点Vを通る直線上の点で,HQ=2pをみたす。線分SS’上に∠VPQ=90°となる点Pをとる。長方が形SBB'S’が直線VQに沿って動くとき,点Pは放物線をかく。

どうでしょう。少し分かりにくいですね。作図器の写真と右の図は縦横が逆になっています。「HQ=2p」の p とはなんでしょうか。動点はどれでしょうか。
「HQ=2pをみたす」については,みたすかどうかではなく,「HQ=2p とすると点Pの軌跡は,HV=x,HP=y と置いたとき $${y^2=2px}$$ と表せる。」ということなのです。それは,このあとの解説にかかれています。
△PHQ $${\sim}$$△VHPより,HQ:HP=HP:HV が成り立つので、
HP$${^2}$$ =HV・HQ
ここで、HV=$${x}$$,HP=$${y}$$ とおくと、上式は$${y^2=2px}$$ と表せる。ゆえに、点Pの動跡は直線 VQを軸とする放物線になる。
また,どれを動点と考えればよいのかは,Web上にある,カラー版の作図器を観察してみることにしましょう。
リンク先に行ったら,「円錐曲線」のページに進みます。その中に「Cavalieri カバリエリ による円錐曲線」があります。これも,写真と図は縦横が異なっていますが,写真をクリックして拡大してみると,動かせるもの,ピンで留められているようなものが,いくらかわかります。
その結果わかるのはつぎのことです。
・長方形SBB'S' は,必ずしも必要ではない。BとB'は作図に関与しない。
棒SS'を安定させるために長方形になっていると考えられる。
・HがVQ上の動点と考えられる。HQの長さは一定。図のPの軌跡が放物線の右半分になる。
実際にCinderellaで作図して確かめてみましょう。
① 点Vを原点としてとり(作図ではA)背景のy軸に合わせて下方に線分を描く。(VHのライン)
② ①の線分上に点を取る。これがHに相当し,動点になる。下の作図順ではC。
③ Qに相当する点を取る。HQは一定なので,円を描いて交点を取る。(D)
④ 中点を加えるツールでADの中点を取り,この点を中心に,Dを通る円を描く。
⑤ 線分ABに垂直でCを通る直線を描き,円との交点をFとする。
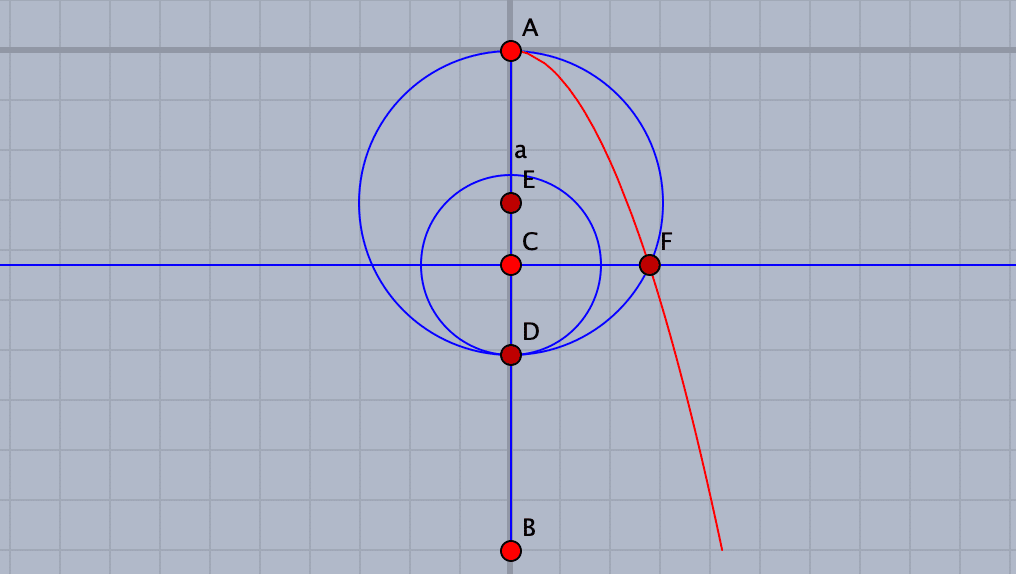
これで必要な点はとりました。AFとDFは結んでいませんが,結べば直角になりますね。軌跡ツールを選んで,動かす点としてC,軌跡を描く点としてFを選べば,放物線の半分が描かれます。
次の図は,点や線を追加し,点の名前も変えて,本の図と同じようにしたものです。

タイトル画面はさらに手を加えて作図器を模したものです。
楕円
図のように長方形 SBB'S'が与えられている。VT=2p,VR=2aとする。角Vが直角である直角三角形RVTがRTに沿って,SS'とVRが交点Hで直交するように動く。点QはVR上の点であり,∠AQH=45°である。線分SS'上に∠VPQ=90°となる点Pをとる。長方形SBB'S'が直線RTに沿って動くとき、点Pは楕円をかく。

カラー版の写真は次のページにあります。
今度は,写真と図とでは上下が逆さまですね。
「VT=2p,VR=2aとする」と,HV=$${x}$$,HP=$${y}$$ とおいて,Pの軌跡の方程式は $${y^2=\dfrac{p}{a}(2a-x)x}$$となる,というのが解説にありますが,誤植があるのと,条件不足なところがあるので引用はやめておきます。△TVRと△AHRが相似であることを使えば,この方程式を導くのはそれほど難しくないでしょう。
Cinderellaで作図するにあたって,何が定点なのかを明らかにしておきましょう。「VT=2p,VR=2aとする」ということは,VT,VRは一定ということです。作図器の写真(上下逆さまにして見てください)では,VRの棒はなく,台に点線が引かれていて,実際にはその左方にある棒が作図に関係するようです。ともかく,△TVRは動かない三角形なので,これを元にして作図しましょう。
① 直角三角形 TVRを適当な大きさで描きます。作図順では△ABCになります。
② AB上に点Dを取ります。これが動点で,本の図(以下,元図)のHになります。
③ 「∠AQH=45°である」ような点A,Qをとるために,Dで垂線を引き,作図のBCとの交点を求め(E),Dを中心として半径DEの円を描き,作図のABとの交点を求めます(F)。作図のEが,元図のA,Fが元図のQに該当します。
④ AFの中点Gをとって,これを中心として半径AGの円を描き,直線DEとの交点Hを求めれば,これが元図のPになります。

これで必要な点はとりました。AHとHFは結んでいませんが,結べば直角になりますね。軌跡ツールを選んで,動かす点としてD,軌跡を描く点としてHを選べば,放物線の半分が描かれます。
次の図は,点や線を追加し,点の名前も変えて,元図と同じようにしたものです。

双曲線
図のように長方形SBB'S' が与えられている。VT=2p、VR=2aとする。角Vが直角である直角三角形RTVがRTに沿って、SS'とVR が直交するように動く。点QはVR上の点であり,∠AQH=45°である。線分SS'上に∠VPQ=90°となる点Pをとる。長方形 SBB'S'が直線RVに沿って動くとき、点Pは双曲線をかく。

今度の写真と図は方向が合っています。条件は楕円とよく似ていますので,同じように作図できるでしょう。