【検証】パイの実でπの値を求めてみる

お世話になります、まーくんです。
よろしくお願いします。

はじめに

「パイ」と「π（円周率）」って読み方が一緒だ。

パイの実の箱を使った工作動画を見ていると、なぜだか突然そう思いました。

よくよく考えてみれば、読み方だけではありません。円周率といえばその名のとおり「円」に関係のある値ですし、お菓子の形も何となく円形ではないですか。

いままで気付きませんでしたが、もしかして２つの「パイ」には決定的な深いつながりがあるのかもしれません。

ということは、パイの実を使って、πが算出できるのでは？

そんな突拍子もないことを考えた私は、パイ（お菓子）とπ（円周率）の関係性を紐解くべく、家の近くのコンビニに向かいました。

はい、買ってきました。
こちらが最もスタンダードな【パイの実　162円（税込）】です。

早速ですが、検証していきたいと思います。

検証

まず「π（3.14）」が使われている有名な公式といえば、以下の２つでしょう。

円周＝直径×π     ①

円の面積＝半径×半径×π     ②

今回は計算を簡単にするために①を使っていきましょう。

この式を変形すると、

π＝円周÷直径　①’

この式を覚えておいてくださいね。

それでは、続いてパイの実を開封し、一つ取り出します。

円周を測っていきます。
※定規は事前にアルコール除菌シートで念入りに拭き、乾かしたものを使用しています。

「これは円周なのか？」、「そもそも六角形だろ」というご意見は一度無視します。

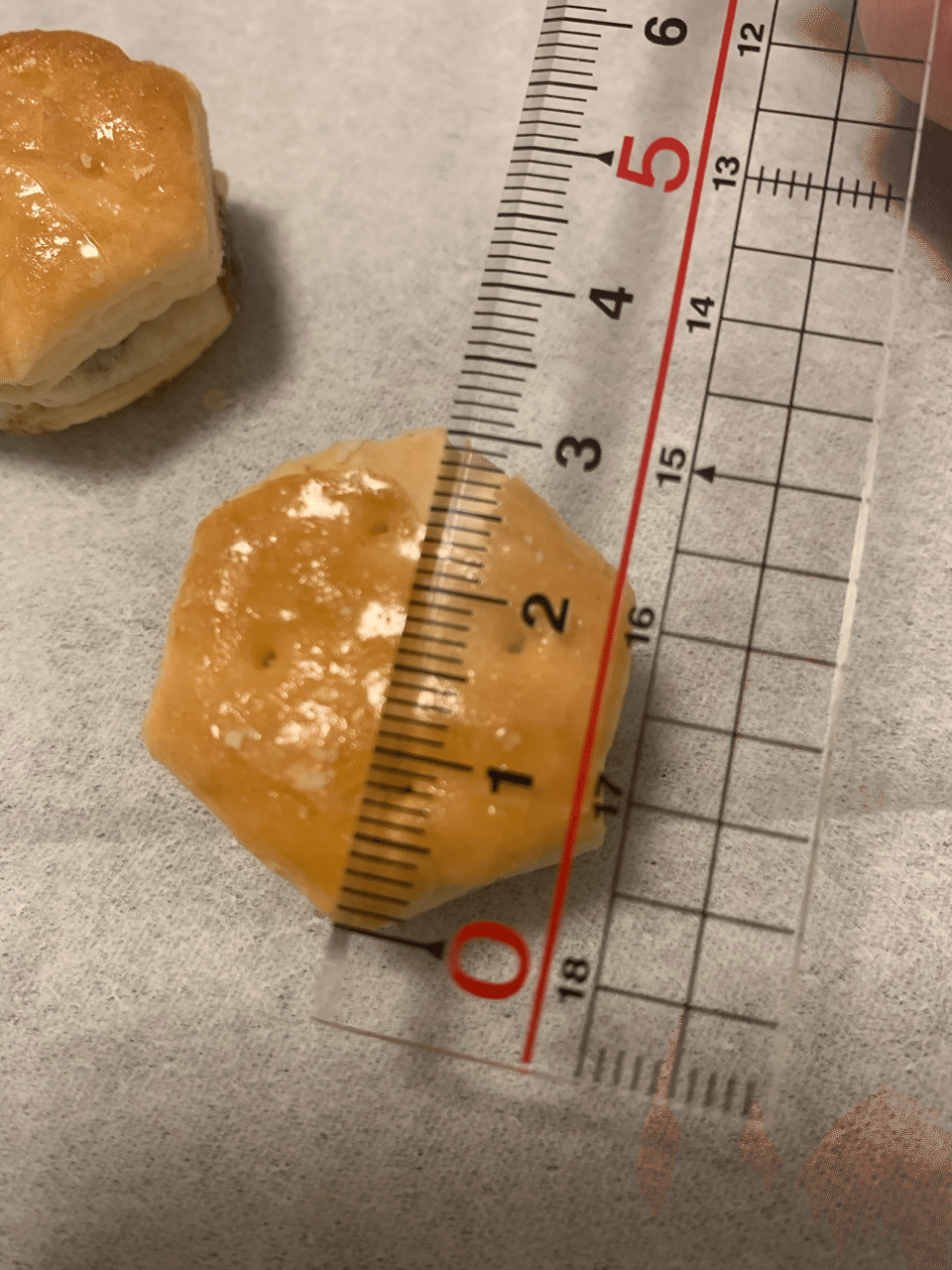
直径を測ります。 その際、対角線の平均を直径とします。

「これは直径なのか？」、「直径の概念とは？」というご意見は一度無視します。

以上の作業を、複数の実に対して繰り返します。

円周！

直径！

…

その結果、以下の結果が得られました。

※測っている時にあまりに美味しそうで無意識で実をいくつか食べてしまいました、すみません。

ここで先ほどの式を思い出してください。

π＝円周÷直径　①’

この式と先ほどの計測値から計算してみると、

πはおよそ「3.03」という結果になりました。

うーん、πは3.14！とはなりませんでしたが、比較的近しい数字になったのではないかと思います。

もう少し母数を増やして計測してみたいですが、結果の数値からもやはり、

「パイ」と「π（円周率）」には関係性がある

ことが検証できたのではないでしょうか。

参考

ちなみに、このπについては、2003年の東京大学の入試問題にもなっているそうです。

円周率が3.05より大きいことを証明せよ。

なんとなく、今回の検証を応用すれば証明できそうな感じがしますね。パイの実は円に近い六角形ですし。

という訳で、みなさまもぜひ、パイの実を使ってπの値を出してみてください。誘惑に負けず全ての実を調べるのは難しいですが笑

以上です。

どうもありがとうございました。