回収率は的中率と〇〇率に依存する？！～波乱レース発生率から導く、驚愕の思考術～

どーも、ＥＮＤです。
クリック頂きありがとうございます。

先にお願いがあります

騙されたと思って、一度最後まで読んでみて下さい

もし読んで頂ければ
「よく聞く、妙味のある（期待値の高い）馬って大体何倍位のオッズから言うのだろうか？」であったり、「本命党、穴党、どちらが正解なんや」であったり、「結局1年間の内、荒れるレースはどれだけあるのだろう」など、これまでぼんやりと疑問に思っていた事、気になっていた事が解決されると思います。

そしてその様な疑問を解決していきながら、結論として

「回収率に直接的に影響を与える指標は的中率と〇〇率である」

という事をお伝えしていきます。

もしこの○○率の重要性を理解頂ければ、あなたの馬券戦術は大きく変更される可能性が高いでしょう。少なからず、私はこれに気付いた時、競馬への考え方を大きく変えました。

では早速やっていきましょう。

1章.ギャンブル（競馬）の仕組み

まず簡単に、ギャンブルの仕組みを説明していきたいと思います。結論から申し上げますと、競馬は

「競馬ファンとのお金の奪い合い」

です。

競馬には控除率というものがあります。控除率とは、胴元（ＪＲＡ）が取っている手数料の割合です。
※単勝・複勝：20％

例）
有馬記念の馬券売上が1億円の場合、ＪＲＡが20％の控除率を徴収し、残り8,000万を馬券的中者に分配される

この控除率が存在する限り、競馬はゼロサムゲームにはなりません。少しゼロサムゲームについて調べると、公営競技もゼロサムゲームと出てきます。ただこれは鵜呑みにするべきではなく、このＪＲＡの控除額も加えてゼロサムゲームと呼んでいます。つまりこの控除額を除けば、競馬参加者からすれば確実にマイナスサムゲームになるという事です

※ゼロサムゲーム：参加者全員の合計終始が常にゼロになるゲーム

ゼロサムゲーム　例）
友人3人で1,000円ずつ出し合い、じゃんけん勝負をする。そしてこのじゃんけんに勝った人は参加費用の合計である3,000円を貰える。

結果は友人Ａの勝利。

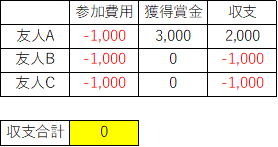
参加者である友人3人の合計収支は0になります。これがゼロサムゲームです。

マイナスサムゲーム　例）
友人Ｄが主催者として、友人Ａ，Ｂ、Ｃで1,000円ずつ出し合い、じゃんけん勝負をする。そしてこのじゃんけんに勝った人は賞金を受け取る。しかし賞金は主催者である友人Ｄの控除率（20％）を差し引いた、参加費用合計の80％とする。つまりじゃんけん勝者が獲得できる賞金は2,400円（3,000円×80％）

結果は友人Ａの勝利。

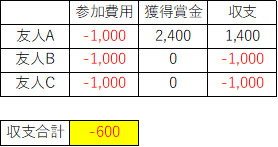
参加者である友人3人の合計収支は-600円になります。これがマイナスサムゲームです。

このマイナスサムゲーム、試行回数を重ねるほど参加者は負けていきます。

「こんなん友人Dがずるい、じゃんけん大会開くほど儲けよる！」って思う人がいるかもしれませんが、事実友人Dが儲ける仕組みになっています。

既にお気づきだと思いますが、競馬に置き換えると

我々競馬ファンは友人ABCの立場、友人DはJRAになります

ただこの控除率にとやかく言っても仕方がないです。考えるべきは獲得賞金である2,400円をいかにして手に入れるか、どうやったらじゃんけんを勝てるのかを突き詰める事です。（もしくはハナから参加しない）

私が伝えたい事は、何も考えず競馬（ギャンブル）をしてしまうと、マイナス収支になる事は必然的であるという事です。だから言って、競馬が絶対勝てないギャンブルかと言えば、私はそうではないと思っています。

「じゃあその勝つ方法を教えろよ」となると思いますが、断言します。

ギャンブルに勝ち方はありません。

もし勝ち方があると言っている方がおられれば、その人は神様か詐欺師です。

ただ面白い事にギャンブルには「負け方」はあります。勝ちたければ、その負け方をいかにして避けるかを考え続け、負けない努力をする事です。

2章.敗者のゲーム

株式投資の本に「敗者のゲーム」という本があります。

めちゃくちゃ簡単に説明すると

敗者のゲーム：相手のミスを待って勝利するゲーム
勝者のゲーム：自らポイントを取りに行って、勝利をつかみ取るゲーム

本ではテニスを例に書かれており、アマチュアはネットに引っかけて自滅する、つまりミスしなければ勝てる。プロはコースぎりぎりを狙い撃ち、ポイントを取らないと勝てない。

同じルールの競技ながら、戦い方は異なります。

そして著者は株式投資は敗者のゲームに属するを主張しています。

私は競馬も敗者のゲームに属すると思っています。なぜそう思うのか、競馬の例を使いながら簡単に説明していきます。

設定）
競馬参加人数：7人
出走馬：3頭
勝率：競走馬A：50％　競走馬B：30％　競走馬C：20％
投資額：1000円/R
控除率：20％
※7000円集まり、JRA控除後、5600を奪い合う

現在の競馬の大衆心理として、競走馬Aに馬券購入者が集まるのが必然です。（前走同舞台2着馬の様なものです）

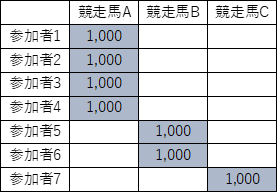
この様に参加者1～4は競走馬A、参加者5～6は競走馬B、参加者7は競走馬Cの馬券を購入したとします。では試行回数を10回（10レース実施）として、それぞれの参加者の回収率をみていきましょう。

参加者1～4）
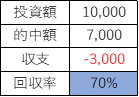
10R馬券を購入するため投資額は10，000円（10R×1,000円）その内5R的中するが、的中時は5,600円を参加者4人で分け合うため1Rあたりの払戻額は1,400円（5,600÷4人）。つまり合計払戻額は7000円（1,400円×5回）

回収率は70％となる

参加者5～6）
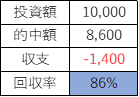
10R馬券を購入するため投資額は10，000円（10R×1,000円）その内3R的中するが、5,600円を参加者2人で分け合うため1Rあたりの払戻額は2,800円（5,600÷2人）。つまり合計払戻額は8,400円（2,800円×3回）

回収率は86％となる。

参加者7）
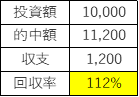
10R馬券を購入するため投資額は10，000円（10R×1,000円）その内2R的中するが、5,600円を参加者1人で分け合うため1Rあたりの払戻額は5,600円（5,600÷1人）。つまり合計払戻額は11,120円（5,600円×2回）

回収率は112％となる。

可能な限りシンプルに説明すると、これが競馬の仕組みです。現実はこれの参加者を競馬ファン全員にし、出走頭数をもっと増やすだけです。

ただここまでを読むと「それなら競走馬Cの馬券を購入するよ」と思いますよね。ただ、多くの方が的中率を追いかけて競走馬Aの馬券を購入しているのが現実です。自然と強い馬に目が行くのは当たり前ですし、前走同条件で好走している馬などの好走率が高いのは間違いではありません。

ただ、過剰人気の馬を買い続ければ負けます。これは持論ですが、現代の競馬において1番人気は常に過剰人気と思っています。なぜなら人気しているが故に馬券を買う人がいるためです。逆に人気のない馬は、人気がないからという理由で馬券は買われません。好走率はある意味、出走馬が確定した時点であらかじめ競走馬で決まります。ただオッズは競馬ファンが作ります。

つまり

人気馬を買う事は競馬において「負け方」に属す可能性が高い

という事です。ただ大半の人はこれに気付かず、競馬の負け方を遂行してくれます。そのため競馬で勝ちたいなら、まず負ける方法はとらない事。例外は当然ありますが

負けたくないなら、極端な言い方をすると「人気馬を買わない事です」

ただ誤解の無い様にお伝えしておくと、人気馬を買う事を全否定している訳ではありません。事実、中には人気馬を買い続けて回収率100％を超している人もいるでしょう。

ここで意識しないといけないのが「購入下限オッズ」です。オッズ何倍以上なら勝負して良い、逆に何倍以下なら勝負してはいけない、という明確な境目です。

人気馬を買いながら競馬で勝ちたい場合、この購入下限オッズを意識する事は必須です。なぜなら、人気馬はこの購入下限オッズが低い事がほとんどだからです。

ではなぜ、人気馬はこの購入下限オッズが低い傾向にあるのか、それは先程説明した様、過剰人気の傾向にあるからです。

ではこの購入下限オッズはどの様に考えるのか、次章で詳しく話していきます。

3章.購入下限オッズ

購入下限オッズとはあなたが

「勝負レースを判断する際の一つの指標」

です。

例えば、あなたの馬券的中率と目標回収率が下記だとします。

的中率：20％
回収率：120％

この時点で一旦はあなたの購入下限オッズは簡単に計算できます。

例）
1Rあたり1,000円馬券購入するとして、計10R購入します。つまり合計投資額は10,000円になります。あなたの目標回収率は120％のため、払い戻し額の合計は12，000円必要です。

そして計10R馬券購入し、的中率20％のため的中レースは2レース。つまり2Rで12000円払い戻せば良いので

6倍（12,000円÷2R÷1,000/R）のオッズなら回収可能です。

この6倍が回収率120％を目指す上での購入下限オッズになります。逆に言うと、このオッズを切っていれば、試行回数を重ねると計算上確実に回収率120％を切ります。

逆の見方をすると「この馬は50％の確率で勝利する！」と思った場合、2倍以上のオッズが付いていれば回収率100％を可能とする馬です。

ただ個人的な意見ですが、動物である馬に対して50％以上の確率で勝利する事を望むのは酷だと思います。あのディープインパクトでさえ負ける事があるのですし、グランアレグリアやアーモンドアイだって、実際安田記念では敗れています。

この動物であるという事を考慮すると、競走馬に対して安定した高い好走率を求める事は酷な話であり、必然的に人気馬は購入下限オッズを割り込む可能性が高いと言えます。

4章.波乱レース発生率

購入下限オッズを理解頂いた上で、ここからはこれまでより、もう少し具体的に馬券購入を想定した内容をお伝えしていきたいと思います。

まず

私のメイン馬券種は「ワイド」

です。理由はいくつかありますが、複勝だとオッズがつかない、着順は騎手や展開一つで簡単に入れ替わってしまうので、予想外の要因を極力減らしたい、極力外れ馬券は買いたくない等々です。まあざっくり言うと、シンプルな馬券の方が良いと判断しているためです。

このワイドはこれまで様々な馬券に手を出してきた中での、現状の結論です。今後変更する可能性は大いにあります。

そのためここからは私のメイン馬券であるワイドを購入前提で書いていきます事、ご了承願います。

私はワイドを買う際、良く人気薄（4人以上）同士で購入します。

※4人＝4番人気　ここからは〇人気馬は〇人と書きます。

ただその際に良く感じていたのが

「4人以上が馬券内に2頭以上絡むという事は、レースとして荒れている。根本的にこの荒れているレースはどれくらいの確率で発生するの？」

というものです。

なぜ気になったかというと、仮にこの確率があまりにも低いと、私の的中率と照らし合わせて回収率100％を超す事は限りなく不可能に近くなる可能性があるためです。

Google先生に色々聞きましたが（ネットで調べた）あまり明確な答えが出てきませんでした。中には近いのがありましたが、それは全て3連単の払い戻し額の大きさで表現されており、それだと着順が影響してしまっています。

私が知りたいデータは、「1年間の内、全レースに対して、4人以上の馬が2頭以上絡んでいるレースの割合」です。もう自分調べる事にしました。それがこちらです。

データ対象期間：2020.01.01~20.12.31
波乱：1人～3人の馬が馬券内に1頭しか来ない事（2頭以上4人以上の馬が絡む事）
小波乱：波乱レースの中で、馬券内4人以上の2頭共が、単勝オッズ49.9倍以下
大波乱：波乱レースの中で、馬券内4人以上の2頭の内、1頭以上が単勝オッズ50.0倍以上
激波乱：馬券内3頭共、４人以上

何と全レースに対し、約45％（小波乱＋大波乱＋超波乱）も波乱レースは発生しています。以外ですよね、印象としてもっと低いと思っていました。

あと以外であったのが、ダートレースの方が高い波乱率である事です。芝は適性、展開などが結果に大きく影響し、ダートは競走馬の能力が大きく影響する傾向にあると思っていました。まあその仮説を否定するデータとまでは言えませんが、面白い傾向ではあります。

そして次に、小波乱レースと大波乱レースを分けた理由についてです。それは穴馬から入る事が多いとはいえ、毎度単勝オッズ50倍以上を買うなんて事はありません。むしろそんな大穴を買う事は少ない位です。そのためそこの割合も把握しておきたく、算出いたしました。（今回の記事ではこのすみ分けはあまり重要ではありません）

では波乱レース発生率が45％と分かったここからは、購入下限オッズの計算に入っていきます。

できる限り分かりやすくお伝え出来る様に頑張りますが、少し計算が複雑に感じる方もおられるかもしれませんので、その場合は計算結果だけ追って頂ければ大丈夫です。（この計算方法は今回伝えたいメインテーマではないため）

前提条件）
開催R数/年：1000R
波乱レース発生率：45％
的中率：15％
※これは波乱レースを的中できる確率、つまりあなたの穴馬予想力と言い換えられます（人気決着時の的中は考慮しない）
投資予算/1R：1000円

※仮定：全ての波乱レースを馬券購入＋波乱レースでしか馬券を買っていない（人気決着レースは100％見送れている）これはほぼ不可能ですが、計算が複雑になるためここではこの様に仮定いたします。（レース見極め率：100％）

後ほど詳しく説明いたしますが、的中率と同じ位、このレース見極め率がめちゃくちゃ重要です。皆さん盲点だと思います。もう一度言います、めちゃくちゃ重要です。

計算）
1年間に1,000R開催され、その内45％が波乱レースです。つまり波乱レースは450R（1000R×45％）存在します。

そのため合計投資金額45万（450R×1000円/R）になります

そしてあなたはその年間450Rある波乱レースを15％の確率で的中できる予想力があります。したがってこの450Rの内、15％の確率で的中するため、68R（450R×15％）のみ的中できるという事になります。

つまりこの68Rで合計投資金額45万を丸々回収すれば回収率100％になります。

購入下限オッズ＝6.6倍（45万÷68R÷1,000）

これらより購入下限オッズは約6.6倍になります。ワイドでこのオッズがつけば、勝負レースとして判断可能であり、試行回数を重ねると回収率100％になります。

逆にこのオッズを切っていれば、馬券購入時点で負けは確定的です。

皆さんはこの数字を見て、どの様に感じましたか？狙えない数字ではない印象に感じましたでしょうか？

ただ注意点として、人気決着には全くかけていない想定。皆さんありますよね？穴から入ったらがちがちの人気決着の時。この確率を考慮されていない状態で最低オッズが6.6倍です。

後ほど、真の最低オッズを説明します。（一遍に説明すると頭こんがらがると思うので、分けています）

5章.では逆に人気決着は？

ここまで読んで頂けた方の中には

「波乱レース発生率は分かったから、逆に人気決着はどれだけあるの？」

と思われる方もおられるでしょう。

それがこちらです。

人気決着：馬券内3頭中2頭以上が1人～3人
超人気決着：馬券内3頭共3人以内
※障害含まない

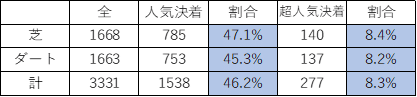
まあこれは当たり前ですが、波乱レースが45％であるならば、人気決着レースは約55％存在します。

ではこの人気決着レースの購入下限オッズを計算していきましょう。

前提条件）
開催R数/年：1000R
人気決着レース発生率：55％（人気決着＋超人気決着）
的中率：40％
※これは人気決着レースを的中できる確率、つまりあなたの予想力と言い換えられます（波乱時の的中は考慮しない）
投資予算/1R：1000円

※仮定：人気決着レース全て馬券購入＋人気決着レースでしか馬券を買っていない。（波乱レースは100％見送れている）
（レース見極め率：100％）

計算）
1年間に1,000R開催され、その内55％が波乱レースです。つまり波乱レースは550R（1000R×55％）存在します。

そのため合計投資金額55万（550R×1000円/R）になります

そしてあなたはその年間550Rある波乱レースを40％の確率で的中できる予想力があります。したがってこの550Rの内、40％の確率で的中するため、220R（550R×40％）のみ的中できるという事になります。

つまりこの220Rで合計投資金額55万を丸々回収すれば回収率100％になります。

購入下限オッズを＝2.5倍（55万÷220R÷1,000）

これらより購入下限オッズは約2.5倍になります。ワイドでこのオッズがつけば、人気決着の勝負レースとして判断可能という事です。

割と印象的には厳しいと思っています。ワイドでも人気決着であれば2倍切ったオッズの時もざらにあります。

ここまでの内容を読んで頂き、この様に思っている方もいるでしょう。

視聴者A：「ENDもう分かったよ。人気決着では期待値が低いから穴馬のワイドを買えってことでしょう？」

END「そんな単純な話ではありません。このnoteで伝えたい事はもっと他にあります！」

まずここまでの話で考慮できていない事が2点あります。

① 穴決着（2頭選びぬく）の的中の難しさ
② レース見極め率

特に最も伝えたい事は「レース見極め率」の重要性です。今の競馬界隈ではこの数字は軽視され過ぎです。

結論から言ってしまうと、購入下限オッズに直接的に影響を与えるのは的中率とこのレース見極め率です。

多くの方は穴馬ら入り、馬券を外した時「人気決着だから仕方ない」「堅いレースには興味がない」「妙味のある馬しか買わないから」と言って終わりますよね。あたかも馬券の買い方や、狙いは間違っていないかの様に。

ただ本当は波乱レースになると予想しているにも関わらず、人気決着になっている場合は馬券的中と同じくらい悔しがるべきなのです。

そのため次の章からは、なぜそんなにもレース見極め率が重要だと言えるのか、さらにその波乱レースの見極め方について伝えていきたいと思います。

記載内容
① 穴馬同士ワイドの的中の難しさ
② レース見極め率の重要性
③ 波乱レースの見極め方
④ 外す勇気（点数を絞る重要性）

大変申し訳ございませんが、無料公開ゾーンはここまでとさせて頂きます。

ここまで約7,000文字強もの量になってしまいましたが、お読み頂き本当にありがとうございます。少しでも皆さんの競馬ライフにお役に立てていれば光栄です。

丁度ここまでの内容で約半分です。

もし「レース見極め率の重要性」さらにその見極め方について少しでも興味を持って頂けましたら、ご購読頂けますと幸いです。

（いいね、RT頂けますと大変嬉しいです）