
DTMer向け float(浮動小数点数)の説明
以前floatとintegerの違いについて、DTMer向けに連ツイしました。この記事はその時の内容をまとめなおしたものです。DTMer向けと書いていますが、その基礎はDTMの世界にとどまるものではありません。ご参考にしていただけると幸いです。
最初にお断りしておくのは、これを知ることで、即、音楽制作に有利になるというものではないということです。興味を持って「floatって結局何なの?」と思っていらっしゃる方に向けた、読み物だとご承知おきください。
floatは浮動小数点数と訳があてられます。その言葉通り、これは小数点を含む数のことなのですが、まずはおさらいを兼ねて、正の整数のお話をさせてください。
まずは整数のおさらいから
そもそもデジタル回路で構成される電子計算機の中枢を流れる信号は、単純にONとOFFの連なりだけで構成されています。ここで例えば、ONに1、OFFに0を割り当ててあげることで、この電気信号の流れを数のように見立てることができます。そしてこの見立てに良く馴染む数の体系として(数学クラスタの皆さん、曖昧な表現ですみません…)2進数という方式が採用されています。
計算機では、2進数の桁の各々をbitと呼びます。8つの桁が集まれば8 bitというわけです。
2進数の各桁は2のn乗の位を表します。図は、ある8bitの数を解釈しているものです。色んな流儀がありますが、ここでは数字列の末尾にBを付けて2進数。Dをつけて私達の日常の数であるところの10進数を表すことにします。

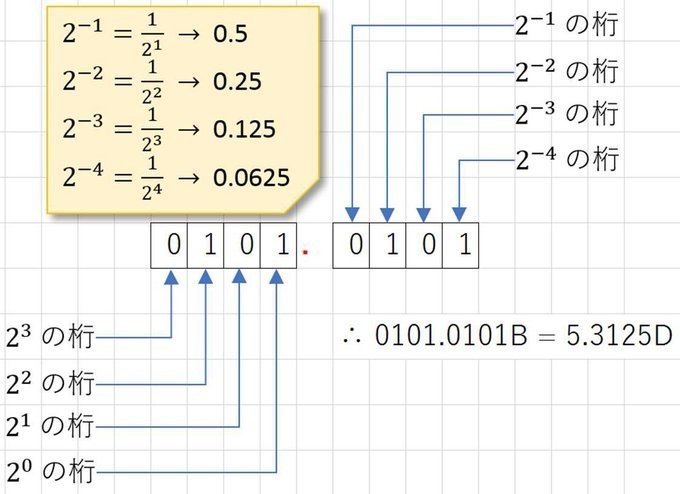
ここまでは割と良くご存知の方も多いと思います。では、二進数の世界で小数をどのように表現できるか考えてみましょう。特にコンピュータの世界では、on/offの二つしかない…と言いましたが、ここでは目をつぶって、小数点の記号が使えるとしましょう。たとえば図のように、0101.0101という2進数の数があったとき、これは10進数ではどんな数を表していると思いますか?

答えが下の図になります。2の-1乗、-2乗、と順に桁の意味が変化します。
詳細は図を見てもらうとして、この数は10進数で5.3125を意味していたわけです。
浮動小数点数では?
ここからいよいよ浮動小数点数の説明に入っていきます。floating point number…つまり、点が浮いてる数…と直訳できそうです。点というのは、ご想像の通り、小数点の点になります。この浮動小数点数の表現の仕方にはいくつかの種類があるのですが、ここでは広く使われているieee754という方式でご説明をしてきます。なおieeeは「あい・とりぷる・いー」と発音します。
ieee754では、小数点を含む2進数で表現された0と1と、小数点の「.」の並びについて、
1.なんちゃら〜
という形になるように小数点の位置を動かしていきます。ここで取り上げた例で言えば、小数点の点を2つ動かすことになります。

ここで、先頭の1.を取り除いた01の並びを仮数部と呼びます。そして、どれだけ小数点を動かしたか、というのを指数部と呼びます。
たとえば、32bit floatと言うのは、この仮数部と指数部のbit長があわせて32bitになるように調整された数のことなんです。

このとき、先頭の01. はデータとして含めなくて良いのか?という疑問もあるかもしれません。その答えは「不要」です。というのは、ieee754では必ず1.〜の形になるように変形するという約束があるからなのです。指数部に「2(2進数で表現したら10ですね)」と仮数部に010101を読み取ったCPUは、まずその先頭に1.を追加して1.010101という形を作ってから、小数点の位置を2つ動かすことになるのです。
floatに対比して使われるinteger(整数)というのは、その名前の通り、「整数」です。つまり、 …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... という風に小数点以下の数を含まない数のことです。たとえばCDは16bit の整数で表現されていますから、サンプリングされた振幅の大きさを0~65,535の65,536段階に分けて表現することができます。これに対してfloat(浮動小数点数)を使えば、100と101の間の100.2とか100.5とか微細な違いを表現できるようになるわけです。
わお。floatすごい💖
とはいえfloatには良いことばかりではありません。私達が普段使っている10進数の小数は、floatでは表現できないこともあるのです。
floatのイケてないトコ
たとえば0.3という数を考えてみましょう。私達10進数の世界に住んでいる私達にはとても簡単な数字です。しかし実は2進数の世界では0.3という数を有限の桁数の中で表現しきることができないのです。
下の図は実際に0.3という数をfloatに変換しようと試みているところです。

この図を見てもらえば分かる通り、私達の世界の10進数の小数を2進数に変換するというのは、剰余(あまり)を2の-n乗の数で割り続け剰余が0になるまで繰り返すという作業であると考えることができます。ここでは16桁分(16ビット分)計算してみましたが、割り切ることができませんでした。実際0.3という数を2進数に変換すると1100110011001100…というビットが並び続けることになるのです。
ここから少しだけDTMerの世界から逸脱します。このような精度の問題はたとえばC言語でfloat, doubleというキーワードで浮動小数点数を使ったときにも出てきます。
例えば以下のようなCのコードがどのようにマシンコードに変換されるかみてみたいと思います。
int test(int argc, char** argv){
float foo = 0.3;
return (int) foo;
}アセンブリ言語の形式を確認してみたいので、-Sオプションを使ってコンパイルしてみます。
% gcc -c -S test.c
% cat test.S
.section __TEXT,__text,regular,pure_instructions
.build_version macos, 10, 15 sdk_version 11, 0
.section __TEXT,__literal4,4byte_literals
.p2align 2 ## -- Begin function test
LCPI0_0:
.long 1050253722 ## float 0.300000012
.section __TEXT,__text,regular,pure_instructions
.globl _test
.p2align 4, 0x90
_test: ## @test
.cfi_startproc
## %bb.0:
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset %rbp, -16
movq %rsp, %rbp
.cfi_def_cfa_register %rbp
movss LCPI0_0(%rip), %xmm0 ## xmm0 = mem[0],zero,zero,zero
movl %edi, -4(%rbp)
movq %rsi, -16(%rbp)
movss %xmm0, -20(%rbp)
cvttss2si -20(%rbp), %eax
popq %rbp
retq
.cfi_endproc
## -- End function
.subsections_via_symbolsLCPI0_0というラベルのついた箇所のコメントを見ていただくと、0.300000012 と書いてあります。コンパイラはその処理の過程で0.3を0.300000012 という形に丸めてしまうのです。先程の図を注意深く見ていただければ、2の-10乗での剰余に0.000000012を追加すれば2の-11乗の数にぴったり一致しますから、ここで割り切れるわけです。
C言語ではfloatは単精度浮動小数点数、doubleは倍精度浮動小数点数と呼ばれています。実際にdoubleを使って同じことをしてみると、目的とする0.3という数との誤差が少なくなっている(=精度がましている)ことがわかると思います。
% cat test.c
int test(int argc, char** argv){
double foo = 0.3;
return (int) foo;
}
% gcc -c -S test.c
% cat test.S
.section __TEXT,__text,regular,pure_instructions
.build_version macos, 10, 15 sdk_version 11, 0
.section __TEXT,__literal8,8byte_literals
.p2align 3 ## -- Begin function test
LCPI0_0:
.quad 4599075939470750515 ## double 0.29999999999999999
.section __TEXT,__text,regular,pure_instructions
.globl _test
.p2align 4, 0x90
_test: ## @test
.cfi_startproc
## %bb.0:
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset %rbp, -16
movq %rsp, %rbp
.cfi_def_cfa_register %rbp
movsd LCPI0_0(%rip), %xmm0 ## xmm0 = mem[0],zero
movl %edi, -4(%rbp)
movq %rsi, -16(%rbp)
movsd %xmm0, -24(%rbp)
cvttsd2si -24(%rbp), %eax
popq %rbp
retq
.cfi_endproc
## -- End function
.subsections_via_symbolsdoubleでの0.3が0.29999999999999999に丸められたことが分かりました。
DTMの世界からfloatを眺めてみると
このように、10進数では正確に表現できる数であっても、2進数にすることで誤差が生まれてしまうことがあります。誤差を許容してでも、段階の刻みを多くしたい(float)か、表現できる幅は狭まるが、クリスプな値を使いたいか(integer)といっても良いかもしれません。
ところで、CDは16bit/44.1kHzのintegerです。その事実に立ち返ると、floatって必要なんだっけ?と思いたくもなります(笑)しかしDAWとしてはfloatが役に立つことがあります。それはプラグインの処理です。
たとえばEQで+3dbブーストするとき、ベルカーブの描く曲線が整数で構成されていたらどうでしょう。微妙にうっすらとしたブーストが全て0に切り捨てられてしまいますが、よろしいですか?←よろしくないです
ですから、少なくともプラグインが処理するデータの形はfloatであることが望まれそうです。そしてプラグインを多段に重ねる時のことを考えると、プラグインの出力データもfloatであれば、びっみょ〜〜〜なブーストの積み重ねも、きちんと音に現れることが期待できるのです。
float🌟大活躍🌟ですね
おわりに
「32bit floatの音が嫌いだ。64bit floatになって、ようやく受け入れられるようになった」
という声を聞くことがあります。本稿で説明したとおり、floatには誤差が含まれることがあります。ですからその真意は 32bit floatではその誤差が気になったが、64bitになって(その誤差が小さくなったために)誤差がもたらす歪みが気にならなくなった ということなのだと思います。
私達が今日利用しているDAWのCPUは64bitで、それらは64bit 浮動小数点数を自由自在に取り回すことができるようになっています。32bit floatから64 bit floatにすることで音質がよくなるのですから、積極的に64bit floatを使っていくべきだろうと考えられます。もちろん64bit floatを使うことでプラグインが使うメモリの量は増えることになりますが、各プラグインは楽曲全体をメモリに読み込むのではなく、作業対象の微小期間を切り出してメモリに展開していますから、64bit floatを使うことでメモリの使用量が莫大に増えるということは考えにくいです。
64bit floatを活用して、DTMライフを楽しんでください。
おまけ1. Cubaseで64bit float処理をするための設定方法について
いきなりお話の粒度が変わってしまうのですが、Cubaseで64bit floatを使うための設定方法についてご説明します。Cubase 9.5から64bit floatでの音声処理をすることができます。この設定は、プロジェクト設定・・・ではなく!!・・・スタジオ設定から行います。
スタジオ > スタジオ設定 > オーディオシステム > 詳細設定 >プロセシング精度 を 64 bit floatに設定することで64bit floatによる音声処理がおこなれれます。

ただし、上記URLに書いてあるとおり、注意事項があります。以下、意訳しながらまとめます。
- 64bit float での処理ではCPUのロードとメモリの使用量が増えます
- VST2 のプラグインやVSTi では32bit floatでの処理がされます
- 64bit floatをサポートするプラグインを確認するには、スタジオ>VST プラグインマネージャー> 画面上段▼アイコンをクリックして>64 Bit Float処理に対応したプラグインを表示 を選択 することで確認することができます。

以下投げ銭です。本文に続きはありません。
お気持ちをいただけたら嬉しいです。
ここから先は
¥ 100
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
