
【全文無料】ゲーム理論から考えるついたて将棋の戦略
こんにちは。wanageeeeです。
ついたて将棋の戦略について今年考えていたことを雑記していきます。
内容の正確性は保証できませんが、将来の自分に向けた備忘録も兼ねて記録に残しておきます。
最後に投げ銭箱を置いてありますが、内容は全て無料で読めます。
前置きとしてのゲーム理論
ミニマックス戦略
自分のことだけを考えていてはゲームは勝てない。相手のムーブを意識したうえで戦略を練る必要がある。
勝とうとするのではなく、負けた時の損失を減らすことを考える。それがミニマックス戦略である。

打者が直球が来るのを予想し、投手が変化球を投げた時の打率が0%。
打者が変化球が来るのを予想し、投手が直球を投げた時の打率が10%。
打者が変化球が来るのを予想し、投手が変化球を投げた時の打率が30%。
表の例で、打者にとってのミニマックス戦略を考える。
直球を予想し、直球を投げてくれれば8割打てる、というのは理想である。
しかし、直球予想で変化球を投げられた場合は打つことはできない。
どんな球を投げられても1割打つことのできる変化球予想が、ミニマックス戦略である。
混合戦略とミニマックス
次に、確率を使ってミニマックスを考える。
先の例で、直球予想と変化球予想をどの割合(確率)にしたときに打者側の損失が最小になるか考える。
すると・・・

直球予想:変化球予想=1:4のとき
直球を投げた時は80%×0.2+10%×0.8=24%
変化球を投げた時は0%×0.2+30%×0.8=24%
となり、損失が最小となる。
すなわち、直球予想:変化球予想=1:4にすることがミニマックス戦略である。
一方で投手側は、どのような割合で投げればよいか。

直球を投げる割合:変化球を投げる割合=3:7のとき、
打者が直球を予想していた場合は80%×0.3+0%×0.7=24%
打者が変化球を予想していた場合は10%×0.3+30%×0.7=24%
となり、損失が最小となる。
すなわち、直球を投げる割合:変化球を投げる割合=3:7にすることがミニマックス戦略である。
以上の結果を見ると、いずれの場合も打率が24%になっている。
ナッシュ均衡
投手側、打者側がともにミニマックスを採ると、上記のように同じ打率が導出される。
このように均衡が保たれている状態をナッシュ均衡という(※)。
均衡点打開の手段
以上より、お互いがミニマックス理論を追及すると均衡点に到達する。
この均衡点を打開することはできないかというのがゲーム理論を実生活に応用するための視点である。
前書きが長くなったが、筆者はこの観点からついたて将棋の考察を試みてきた。
筆者は、「相手のありうる配置の範囲」を狭め、「相手目線で自分のありうる配置の範囲」を広げることを心がけている。
先の例で言うと、自分が打者だとしたら、投手の投球動作の癖などから「相手が変化球を投げてくる」確率を限りなく0に近づけていくイメージ。
逆に相手には自分の癖や思考をなるべく見抜かせずに予想の割合を読ませないようにしている。
ここからは、配置の範囲のことをポーカー用語を借りて「レンジ」と呼ぶ。
相手目線のレンジは広げ、自分目線のレンジは狭める。
シンプルだが、強力な戦略である。
以下、具体例を一部紹介する。
自分目線のレンジを狭める戦略例
角の使い方を3パターンに分ける
角の使い方を居角・引き角・端角の3パターンに分ける。
角の使い方から、あり得る駒組の組み合わせ(コンボと呼ぶ)を絞っていく。
over囲いと呼ばれる形からの一変化である。

21手目▲3四歩。ここで△3四歩と突かれていないことから、端角・引き角の可能性がやや高まっている。

25手目▲1三桂不成。ここで端角が消え、引き角の可能性が高まる。
引き角だった場合、このような配置が予想される。
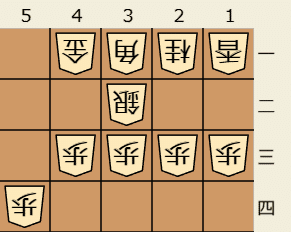
▲3三歩成△同Xに対し、▲3二歩と打つ。反則だったため、3二銀、3三桂の配置が予想できる。仮に反則にならなかった場合は、△3三同銀の可能性が出てくる。


3三桂を逃がすのに自然な選択である△4五桂を狙って▲4五歩。
仮に空ぶったとしても、▲3三歩成~▲4四歩~▲4三歩成とすれば、右の金銀と差し違える公算が高まるのでよい。
角の通過反則を活用してレンジを狭める
筆者の実戦より(符号は先後逆)。

△7六歩と取られた局面。▲2二角成としたいところだが、△3三歩型のためそれはできない。そこでひと工夫加えた。

▲5五角~▲8二角成。
△7六歩から相手の主戦筋が7筋と考えられたので、▲8二角成ができないか試した。反則だったので6四か7三に最低1枚駒がいることがわかる。
以下のように進んだ。
長手数進めたが、まず気にすべきは相手の玉位置である。
▲4四馬で歩を取って王手がかかっている。

4三、5四、6二、7一が玉位置候補。
4三玉は、▲2二同角成△4四歩▲1一馬△4三玉▲4四馬というレアケースしかない。
6二玉、7一玉に王手がかかったパターンもあるが、そうすると今取った△4四の駒は何なのか、という話になる。
右銀を取れていることを考えると、飛車か金である。
飛車なら4二の飛車が取りに来たことになるが(4一飛なら▲1一馬を取れているはずなのでないだろう)、△7六歩との整合性が合わないことと、△4四歩をもっと早く突いておかしくないことから可能性は低そう。
金ならどこにいた金で取ったのか、という話になる。
△5三金ならそもそも王手がかからない。
△5四金なら△5五歩とセットになる(7一と6二で王手がかかるなら、△5三歩はありえないので)のでほぼ無い。
△4三金だと、▲2二同角成△4四歩▲1一馬△4三金▲4四馬というパターンしかない。
そうすると、△4四同飛or同金は相当なレアケースであると考えられ、6二と7一の可能性がほぼ消える。
よって、▲4四馬の王手は△5四玉に対してかかった可能性が高いと読める。
そして、序盤の角通過反則がこの裏付けになっている。
つまり、△5四玉は6三か6四から来たことがわかるので、△6四歩を突いていた場合、△6三玉~△5四玉ルートがほぼ確定するが、▲8二角成できていないので△6四歩と指している可能性をかなり高く見積もれそうということである。

そのうえで実戦は、▲6三角と指した。
△6四歩と突いていたことが確定し、△4四玉もほぼ確定したといえる。

5四や5二への退路を断ち、左辺に逃げづらくしている。以下制勝。
角の通過反則から得られた情報を複利で活用できた一局だった。
確定手+初期位置への駒移動からレンジを狭める
居飛車で仕掛けられて、不明手は4手。この手で玉回りに手をかけていることがわかっているとする。相手陣はどのような形をしているだろうか。
例えば以下のような陣形を想像できる。




例えば、▲3四歩と突いて歩が取れなければ△3三歩が確定するので、上3つは消えるし、
▲7一と で銀が取れて△同Xとされなければ金が7一に利いていない△7一銀・6二金や△7一銀・5二金が考えられ、上2つの可能性が高まるし、
▲7一と で銀が取れなければ△6二銀か△7二銀している可能性が出てくるので上から3つ目の可能性が出てくる
というように、考え得るコンボからレンジを狭めることができる。
大事なのは、初期位置に駒がいるかどうか、という点で、
7一に駒がいない→銀を動かしている
6一に駒がいない→金を動かしている
6一に駒がいない、かつ王手もかからない→金も玉も動かしている
というように情報を掴んでいく。
仕掛け時の不明手数≒玉まわりに手をかけた手数は、10手台に戦いが起こった際の最重要情報と考えてよい。
というのも、仕掛け後に玉まわりを整備するプレイヤーは少なく、終盤の寄せや一点読みに生かすことができるからである。
攻め駒のコンボ読みからレンジを狭める
ついたて将棋の攻めは、特定の地点に複数の駒の利きを集める「足し算の攻め」が基本。
逆の立場に立つと、相手の足したい地点がわかれば、受けやすくなる。
桂馬の利きから狙いの地点を考える手法がその一例である。

5六桂を取れた局面。警戒すべき地点は4八と6八。具体的には・・・?

5九に角や銀を打たれている可能性が高い。
5六桂を取れた時点で、以下のような図面を想像できるかどうか。

相手目線のレンジを広げる戦略例
逆に、相手にはレンジを絞らせないことが大切である。
金銀を端に逃がす
古戦場で使い道のなくなった金銀を端に逃がすのは、1つの手法である。

2九の銀を処置したいが、▲3八銀と上がると、△2六歩~△2七歩成~△3八とのように自然に銀を取られる恐れが高い。一方、▲1八銀と端に逃がすと、これ以上の働きは期待できないものの、自然に銀を取られるリスクを低減できる。
端への金銀の移動は、駒損しないだけでなく、相手に駒位置を把握させない(この例で言えば銀のレンジを狭めない)効用もある。
主導権を握った状態で不明手を作る
居飛車速攻後に意図的に不明手を作ることで、相手に手がかりを与えずにレンジを広げる指し回し。
不明手を作ることで当然お互いのレンジも広がるのだが、先行された相手は守勢になりがちなことから、速攻後の戦略としては有効である。
相手の狭めた(はずの)レンジを逆用する
盲点を突くことで、相手の狭めたはずのレンジを広げることもできる。
索敵済地点への玉移動は最たる例である。
↓5月にviewerに投稿した自戦記。
まとめ
「ミニマックス戦略を採った上で到達する均衡を打破する目的で、自分のレンジを広げ、相手のレンジを狭める」というのが、私の採用するついたて将棋の基本戦略である。
(※)ナッシュ均衡には、相手が動かない限り均衡が保たれるという問題点がある。自分の選択と相手の選択の相互作用が考慮されていないからである。例えば、投手が直球を投げる割合:変化球を投げる割合=3:7を維持し続けている場合、極端な話、打者は全球直球が来ることを予想をしても、全球変化球が来ることを予想しても、打率は2割4分のまま、ということである。そのため混合戦略におけるナッシュ均衡は最適な戦略ではないし、実用的な考え方とは言い難いが、理論上均衡状態が生まれることを示すために提示している。
なお、本記事を書くにあたり以下の書籍を参照している。
・一歩ずつ学ぶ ゲーム理論 -数理で導く戦略的意思決定-(裳華房)
・新版 ゲーム理論トレーニング(かんき書房)
ここから先は
¥ 132
この記事が気に入ったらチップで応援してみませんか?
