テブナンの定理

キルヒホッフの法則や重ね合わせの理で回路を流れる全電流を計算することができますが、連立方程式を解く必要があります。テブナンの定理は、複雑な回路の一部を流れる電流を四則演算で計算することができます。
テブナンの定理は複雑な回路を等価回路に変換して電流を求める定理です。

上図のように複雑な回路の抵抗Rに流れる電流を求める際に、等価電源E0と等価抵抗R0の等価回路に変換します。

手順

1.電流を求めたい部分を切り離します。
2.等価電源E0を求めます。
3.等価抵抗R0を求めます。
・回路内部の電圧源はすべて短絡して除去します。
・回路内部の電流源はすべて開放して除去します。
4.等価回路に変換します。
5.目的の電流の以下の式で求めます。

この式がテブナンの定理を表しています。

等価電源の求め方

上図の回路で、R3に流れる電流値を求めるとき、点ab間の電源電圧を計算します。
このとき、R3を回路から切り離した状態を考えます。
R3を切り離すと上図の回路になります。
端子a、bは開放されているので、電流は流れません。
この回路を流れる電流をIとして、b点を基準と考えると、E1とR1の接続点は、E1の電圧になります。そこからさらに電流IがR1を通過した際にI・R1の電圧があります。
キルヒホッフの第二法則によって、「閉回路内の起電力の和」が「その閉回路内の電圧降下の和」に等しくなります。

起電力E1の極性は電流の流れに順方向です。E2は逆方向になります。順方向、逆方向は仮に決めた電流Iによるので、最後の値がマイナスになる場合は、電流の方向が想定と逆になっていたことになります。
起電力は、E1-E2になります。電圧降下は、R1・I+R2・Iになります。これが等しいので、この回路を流れるの電流は、

となります。

上の図で抵抗Rの端子は、それぞれ電源Eのプラスとマイナスに接続されています。Rに電流Iが流れると、Rによる電圧降下が発生します。
Rの両端の電圧は、電流が流入する側が高く、流出する側が低くなります。

この回路に流れる電流は、以下の通りです。

電流値に抵抗値をかけるとR1の電圧降下になります。

a点の電圧E0は、起電力E1とR1の電圧降下によって

この式にR1の電圧降下を代入すると

となります。

等価抵抗の求め方

等価抵抗は回路から電源を取り除き、合成抵抗を求めます。

電源を取り除くと上の回路になります。
電源を取り除くとき、電圧源は取り除いたあとに短絡します。
電流源はそのまま開放しておきます。

取り除いたあとを短絡して、R1、R2合成抵抗を求めます。

電流の求め方

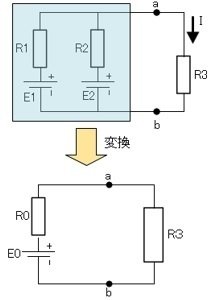
電源E1、E2を等価電源E0、R1、R2を等価抵抗R0に置き換えて回路を簡略化します。
等価電源、等価抵抗をテブナンの定理の公式に代入します。

となり、R3に流れる電流を求めることができます。