連立方程式

キルヒホッフの法則自体は簡単なのでは理解できても、連立方程式で躓くと聞いたことがあります。
電気回路で、回路の各部の電圧や電流の値を求めようとすると、それらを変数とした連立方程式を立て，その解を求める計算を行うことがあります。また、電気回路に限らず連立方程式は、さまざまなところで使用されています。

複数個の未知数を含み、かつすべての方程式が未知数についての1次方程式からなっているような方程式を連立1次方程式といいます。未知数の個数が2個、3個により、2元連立1次方程式、3元連立1次方程式といいます。下の例では、x、 yを未知数とする2元連立1次方程式です。

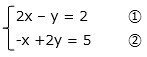
連立1次方程式を解くとは、与えられた方程式をすべて同時に満足する未知数の値を求めることです。そのためには、代入法や加減法あるいは等置法などといった解法があります。それらを用いて順に未知数を消去していき、最終的に1元方程式として解を導きます。

代入法による解法

上の例では、①の式を整理し、未知数yを求める式に変換します。
2x / y = 2　　　　両辺から2xを引く
-y = -2x + 2　　　両辺に-1をかける
y = 2x -2　　　　 ③
未知数yを求める式ができたので、②の式のyに代入します。これで、未知数yを消去することができます。
-x +2(2x-2) = 5
x = 3　　　　　　 ④
④の式を③の式に代入して未知数xを消去します。
y = 2 × 3 ? 2
y = 4

加減法による解法

加減法とは、連立方程式を構成している式同士の足し算・引き算をすることによって、文字の数を減らして、解を探す方法です。

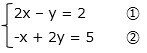
上の例では、同じ係数が無いので、①の式を2倍にします。
これにより、y項が-2と+2になります。

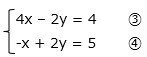
項目ごとに加算を行うことで、y項が消去されます。

4x + ( -x) = 3x
-2y +2y = 0
4 + 5 = 9
3x = 9
X = 3

倒置法による解法

連立方程式の計算で一番使われる解方は加減法です。次に使われるのが代入法です。
さらに倒置法という解法があり、これが使えると簡単に解ける場合があります。

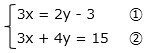
上の方程式で、3xに着目し、②の式を変換します。
3x = 15 – 4y
二つの式の左辺が3xになったので、等号で結ぶことができます。
15 – 4y = 2y -3
両辺を2yで引き、15を引くことで、y項を左辺に移動できます。
-4y -2y = -3 - 15
-6y = -18
y = 3
y = 3を代入すると
3x = 2y -3
3x = 2 × 3 – 3
3x = 3
x = 1

キルヒホッフの法則の応用で使用した回路に具体的な値を設定して実際に電流を計算します。

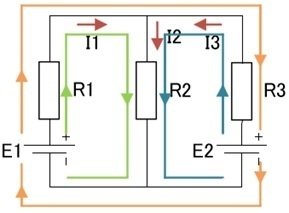
上の回路でR1=10kΩ、R2＝10kΩ、R3=20kΩ、E1=60V、E2=5Vとします。
回路に流れる電流を想定し、連立方程式を作ります。これも、キルヒホッフの法則の応用で作った方程式をそのまま使います。
代入法、加減法を用いて、I1を求めることができます。I1が分かると、代入法でI3が求まります。
I1とI3が分かるとI2も求まります。
ここから先は、有料にさせていただきます。有料記事では、式の変換等の説明を追加しています。
自分で計算した結果を確認したいときは、LTspiceなどの回路シミュレータを使うと確認が可能です。

抵抗値の単位はkΩです。計算する際に1000倍する必要がありますが、桁が大きくなって計算がややこしくなります。幸いに全部がkΩなので、そのまま計算して最後に1000で割ります。つまり、算出された電流値をmAとします。

連立方程式の1番目の式を2番目の式に代入します。

E1 = R1I1 + R2I2
E1 = R1I1 + R2(I1+I3)

ここで、数値を代入します。

60 = 10I1 + 10(I1+I3)

式を変形します、

60 = 10I1 + 10I1 + 10I3
60 = 20I1 + 10I3　①

3番目の式にも数値を代入します。

60-5 = 10I1 - 20I3
55 = 10I1 - 20I3　②

①の式からI3を消したいので、①の式の両辺を2倍にします。

120 = 40I1 + 20I3　③

加減法を使って、I3を消します。
③の式はI3がプラス、②の式はI3がマイナスなので、右辺同士、左辺同士を加算すると、I3が消えます。
   120 = 40I1 + 20I3
+) 55 = 10I1 - 20I3
ーーーーーーーーーー
　175 = 50I1

左右を入れ替えます。

50I1 = 175

両辺を50で割るとI1の値を求められます。

50I1 / 50 = 175 / 50
I1 = 3.5

②の式にI1を代入すると、I3を求めることができます。

55 = 10I1 -20I3
55 = 35 - 20I3

両辺に20I3を加えます。

55 + 20I3 = 35

両辺から55を引きます。

20I3 = 35 -55
20I3 = -20

両辺を20で割ります。

20I3 / 20 = -20 / 20
I3 = -1

連立法廷式の1番目の式にI1、I3を代入します。

I2 = I1 + I3
i2 = 3.5 + (-1)
I2 = 2.5

I1、I2、I3の値が算出されました。
I2がマイナスになっているので、想定した電流とは逆に流れています。

はじめに説明した通り、算出された値は、1000倍になっているので、単位を調整します。

I1 = 3.5mA
I2 = 2.5mA
I3 = 1mA