2進数の加算を行う回路です。
全加算器と半加算器があります。
どちらも1桁の加算を行う回路ですが、半加算器は、下位桁からの繰り上がりを考慮しません。全加算器は考慮します。
複数桁の加算を行う際には、最下位桁に半加算器を使用し、2桁目以上に全加算器を使用します。
半加算器
2進数の同じ桁どうしの演算をして、演算結果(S:Sum)と桁上がり(C:Carry)を出力します。
真理値表は以下の通りです。

SはAとBの値が異なる場合に1になりますから、排他的論理和、CはAとBが1の場合にだけ1になるので、論理積になります。
論理式は以下の通りです。

論理回路は以下の通りです。
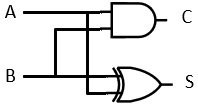
全加算器
全加算器は、2進数の同じ桁どうしの演算をして、下位からの演算結果(S:Sum)と桁上がり(C:Carry)を出力します。
全加算器は、同じ桁どうしの加算を行い、その演算結果と下位桁からの桁上がりを加算します。
真理値表は以下の通りです。

論理式は以下の通りです。

論理回路は以下の通りです。

複数桁の加算回路
加算は同じ桁どうしで行います。
最下位の桁は下からの桁上がりが無いので、半加算器を使用します。
最下位以外の桁は下位桁からの桁上がりが必要になるため、全加算器を使用します。
回路を簡略化するため、すべての桁に全加算器を使用し、最下位桁の桁上がり入力を常に0にする場合もあります。
下の図の右の回路と左の回路は同じ動作をします。
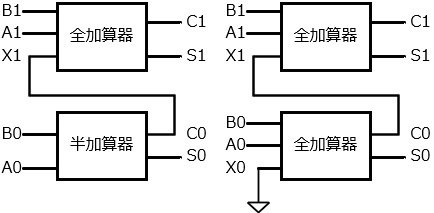
全加算器の改良
全加算器の論理式が複雑なので簡単にできないか考えます。
まずは、カルノー図を使って式を簡略化できないか試します。
Sの式のカルノー図は以下の通りとなりますが、グループ化できるとこがありません。
入力が3個のときは、2個と1個に分けて表を作ります。
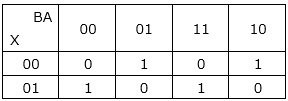
Sの式は、カルノー図を使って簡略化することができませんので、別の方法で式を簡単にします。

簡略化した式から回路を設計します。
Sを出力する回路は以下のようになります。

この回路にCを計算する回路を追加します。
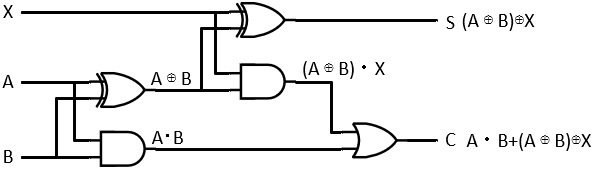
完成した回路を見ると、下の図のように半加算器を2段に接続したものであることが分かります。

ここから先は
¥ 100
この記事が気に入ったらサポートをしてみませんか?
