
平成23年度 機械科目 問16 電験3種過去問
問題

考え方
この問題は、他励直流電動機に関する問題である。等価回路を書いて条件を整理しながら考える。(b)は、回転速度の変化に対する機械的出力の増加を考慮して、各条件を考える。
解答例
(a)
等価回路を図1に示す。

図1より、電機子電圧$${V}$$は、
$$
\begin{align}
V &= E_{1}+R_{a}I_{a}\notag\\
&= 200 + 0.4\times 20=208\,{\rm{V}}\tag{1}
\end{align}
$$
と求まる。よって、(a)の答えは(5)である。
(b)
問題文より、トルク一定で回転速度が増加すると、機械的出力が増加しないといけない。回転速度は、$${600\,{\rm{min^{-1}}}}$$から$${1320\,{\rm{min^{-1}}}}$$に$${2.2}$$倍になっている。よって、機械的出力も$${2.2}$$倍にならないといけない。回転速度が$${1320\,{\rm{min^{-1}}}}$$の時の機械的出力$${P_{m2}}$$は、
$$
P_{m2}=2.2\times 200\times20=8800\,{\rm{W}}\tag{2}
$$
となる。
誘導起電力$${E}$$は、
$$
E= K_{g}\Phi N\tag{3}
$$
$${K_{g}}$$:比例係数、$${\Phi}$$:磁束、$${N}$$:回転速度
で求められる。
問題文より磁束は、界磁電流に比例するので、回転速度が$${1320\,{\rm{min^{-1}}}}$$の時は、
$${\frac{1}{2}}$$倍になる。また、回転速度は、$${2.2}$$倍になっているので、回転速度が$${1320\,{\rm{min^{-1}}}}$$の時の誘導起電力$${E_{2}}$$は、
$$
E_{2}=\frac{1}{2}\times 2.2\times 200=220\,{\rm{V}}\tag{4}
$$
と求まる。
よって、電機子電流$${I_{a}}$$は、式(2)と式(4)より、
$$
I_{a} =\frac{8800}{220}=40\,{\rm{A}}\tag{5}
$$
と求まる。回路図で示すと図2になる。
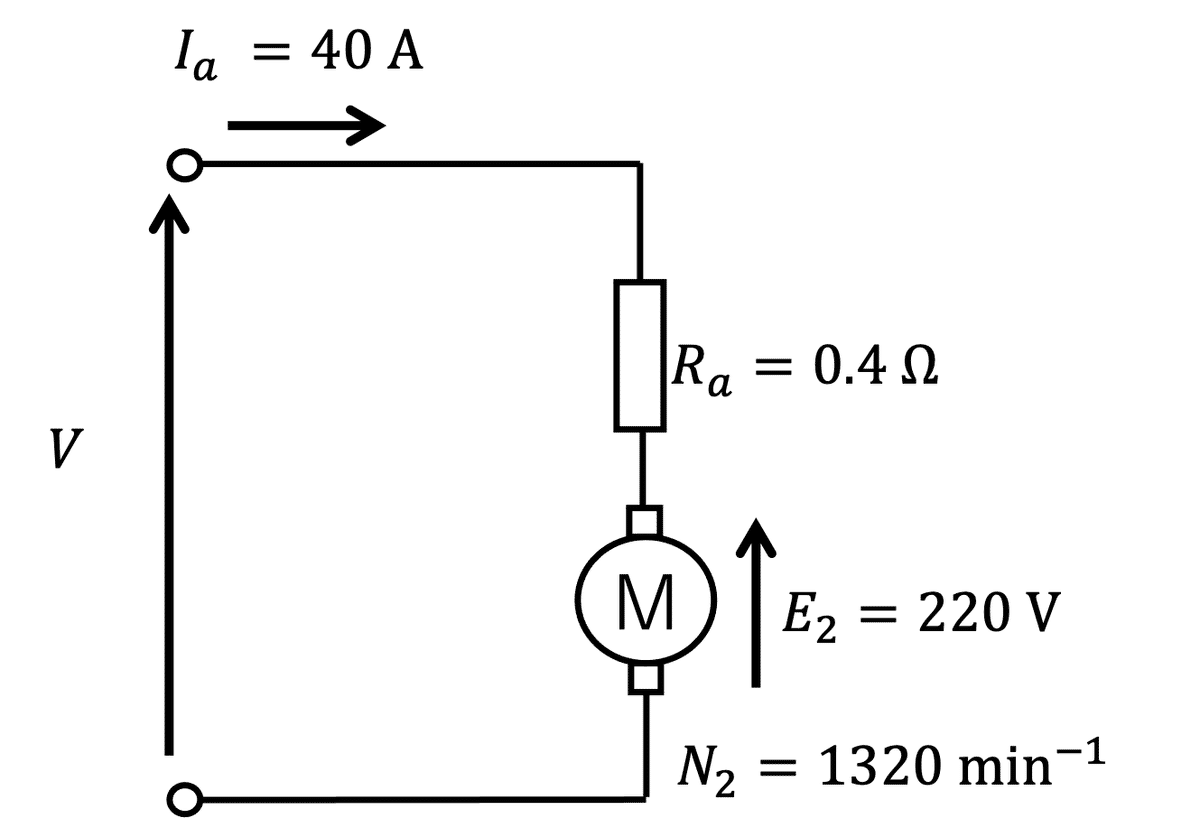
図2より、電機子電圧$${V}$$は、
$$
\begin{align}
V &= E_{2}+I_{a}R_{a}\notag\\
&= 220+40\times 0.4=236\,{\rm{V}}\tag{6}
\end{align}
$$
と求まる。よって、(b)の答えは(3)である。
関連記事
等価回路でみる直流電動機
https://note.com/elemag/n/n28872c3b3273?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
