
令和2年度 理論科目 問6 電験3種過去問
問題
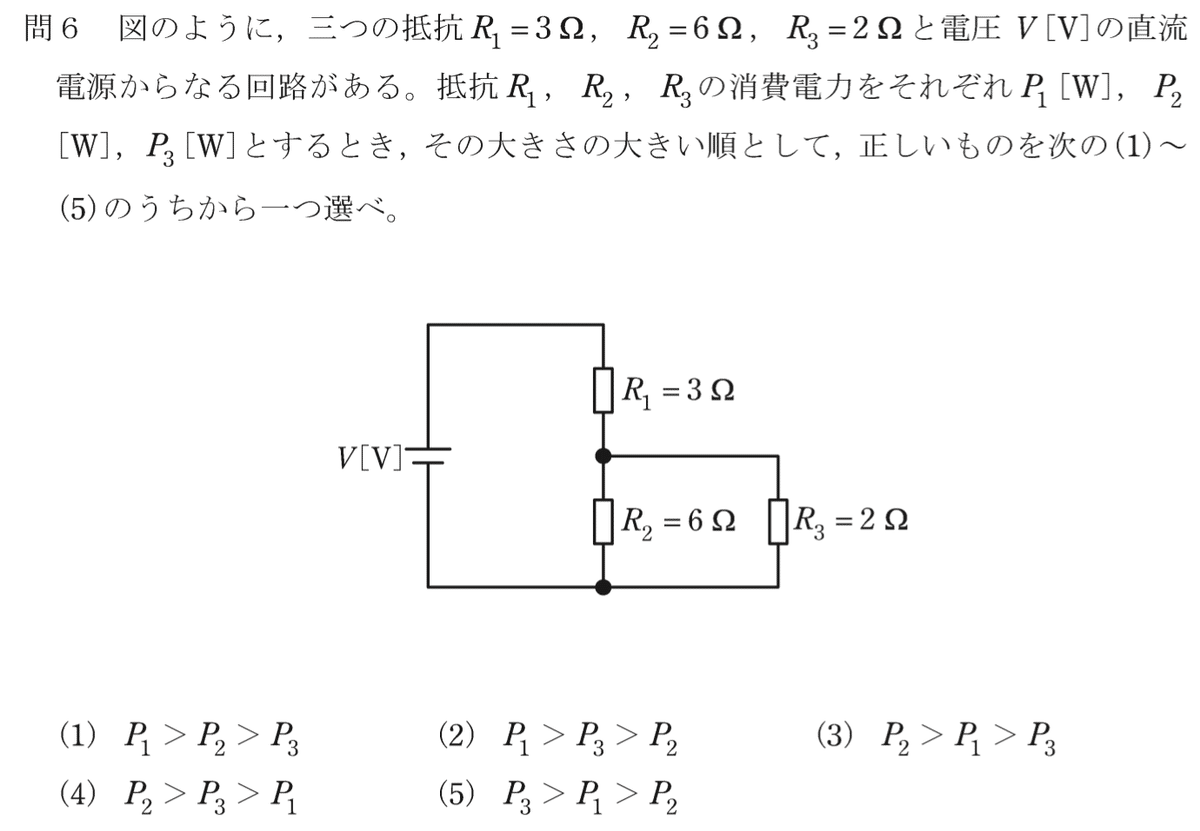
考え方
この問題は直流回路に関する問題である。
消費電力$${P}$$の式は、電圧を$${V}$$、電流を$${I}$$、抵抗を$${R}$$とすれば、
$$
P=VI=RI^{2}=\frac{V^{2}}{R} \tag{1}
$$
となる。
ここでは、電源電圧$${V}$$と抵抗$${R}$$がそれぞれ示されていることから、
$$
P=\frac{V^{2}}{R} \tag{2}
$$
を使って考えると良さそうだ。
また、$${R_{1}}$$と$${R_{2},R_{3}}$$は直列であるから分圧することに気を付ける。
解答例
まずは、消費電力を考えるのに必要な電圧を計算する必要がある。$${R_{2},R_{3}}$$の並列回路の合成抵抗$${R_{23}}$$は、
$$
\begin{align}
R_{23} &= \frac{R_{2} \times R_{3}}{R_{2}+R_{3}} \notag \\
&= \frac{6 \times 2}{6+2} \notag \\
&=\frac{12}{8}=\frac{3}{2} \tag{3}
\end{align}
$$
であるから、抵抗$${R_{1}}$$にかかる電圧$${V_{1}}$$は、
$$
\begin{align}
V_{1} &= \frac{R_{1}}{R_{1}+R_{23}} V \notag \\
&= \frac{3}{3+\frac{3}{2}} V \notag \\
&= \frac{3}{\frac{6+3}{2}} V \notag \\
&= \frac{6}{9} V \notag \\
&= \frac{2}{3} V \tag{4}
\end{align}
$$
抵抗$${R_{2},R_{3}}$$にかかる電圧$${V_{23}}$$は並列回路であるから同じである。また、電源電圧$${V}$$は、$${V_{1}}$$と$${V_{23}}$$を足したものであるから、
$$
\begin{align}
V &= V_{1} + V_{23} \notag \\
V_{23} &= V-V_{1} \notag \\
&= V-\frac{2}{3}V \notag \\
&= \frac{1}{3} V \tag{5}
\end{align}
$$
ここからようやく消費電力を考える。
式(4)、(5)をそれぞれ2乗すると、$${{V_{1}}^{2} = \frac{4}{9} V^{2}}$$、$${{V_{23}}^{2} = \frac{1}{9}V^{2}}$$である。よって各消費電力は、
$$
\begin{align}
P_{1} &= \frac{{V_{1}}^{2}}{R_{1}} = \frac{\frac{4}{9}V^{2}}{3} = \frac{4}{27} V^{2} \tag{6}\\
P_{2} &= \frac{{V_{23}}^{2}}{R_{2}} = \frac{\frac{1}{9}V^{2}}{6} = \frac{1}{54} V^{2} \tag{7}\\
P_{3} &= \frac{{V_{23}}^{2}}{R_{3}} = \frac{\frac{1}{9}V^{2}}{2} =\frac{1}{18} V^{2} \tag{8}\\
\end{align}
$$
となる。$${P_{2}}$$が1番小さいことは明らかである。$${P_{1}}$$は分子を1にするために分母を4で割ると$${P_{3}}$$より、大きいことがわかる。
よって、消費電力の大小は、
$$
P_{1} > P_{3} > P_{2}
$$
となり、(2)が答えになる。
$${P_{3} ,P_{2}}$$は実際に値を出さなくても大小が分かる。式(2)より、電圧が同じであれば、抵抗が小さいほど消費電力が大きい。今、抵抗の大小は$${R_{3} < R_{2}}$$であるから、消費電力は、$${P_{3} > P_{2}}$$である。
もしも、抵抗$${R_{1}}$$と抵抗$${R_{3}}$$が等しいとすれば、消費電力$${P_{1}}$$は電圧の大小比較のみで答えが出せる。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
