
令和元年度 理論科目 問5 電験3種過去問
問題

考え方
この問題は直流回路に関する問題である。
分圧の考え方を用いて解いていく。電位の基準に注意すること。
解答例
並列回路となっている部分の合成抵抗$${R_{1}}$$は、
$$
\begin{align}
R_{1} &= \frac{(20+20+20)\times 60}{(20+20+20)+60} = 30 \, Ω\tag{1}
\end{align}
$$
となる。
よって、図1のような回路となる。
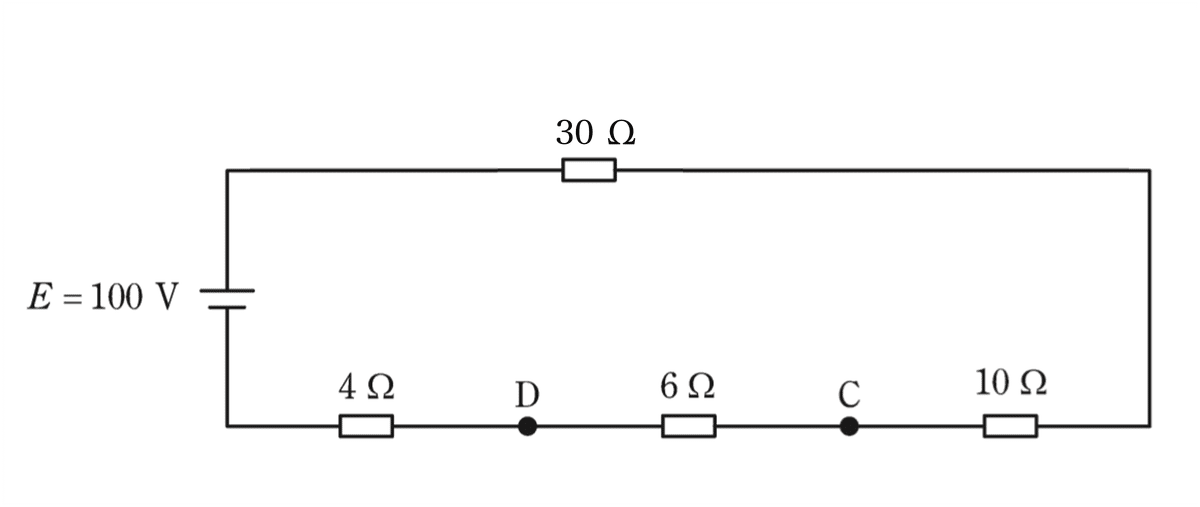
図1より点Dと点Cの電位$${V_{\rm{D}}}$$および$${V_{\rm{C}}}$$は、分圧の式を用いて、
$$
\begin{align}
V_{\rm{D}} &= \frac{4}{4+6+10+30}\times 100 = 8\, \rm{V}\tag{2}\\
V_{\rm{C}} &= \frac{4+6}{4+6+10+30}\times 100 = 20\, \rm{V}\tag{3}\\
\end{align}
$$
となる。
また、合成抵抗$${R_{1}}$$にかかる電圧$${V_{1}}$$は、
$$
\begin{align}
&\notag\\
V_{\rm{1}} &= \frac{30}{4+6+10+30}\times 100 = 60\, \rm{V}\tag{4}
\end{align}
$$
となる。

図2に示すように青点で示す点Eが$${0\,\rm{V}}$$である。また、赤点の点Xが$${100\,\rm{V}}$$である。したがって、合成抵抗$${R_{1}}$$にかかる電圧$${V_{1}}$$が$${60\, \rm{V}}$$ということは、点Yの電位は$${100-60=40\, \rm{V}}$$となることに注意する必要がある。
次に点Aおよび点Bについては、合成抵抗$${R_{1}}$$にかかる電圧$${V_{1}}$$が$${60\, \rm{V}}$$であり、各$${20\,Ω}$$の抵抗で等しく分圧するので、各$${20\,Ω}$$の抵抗の電圧は、$${20\,\rm{V}}$$となる。
よって、点Bの電位$${V_{\rm{B}}}$$は、点Yの電位に$${20\,\rm{V}}$$を足して、$${60\,\rm{V}}$$となる。また、点Aの電位$${V_{\rm{A}}}$$は、点Xの電位から$${20\,\rm{V}}$$を引いて、$${80\,\rm{V}}$$となる。
A-D間の電位差の大きさは、
$$
V_{\rm{A}}-V_{\rm{D}} = 80-8 = 72\,\rm{V}\tag{5}
$$
となる。
B-C間の電位差の大きさは、
$$
V_{\rm{B}}-V_{\rm{C}} = 60-20 = 40\,\rm{V}\tag{6}
$$
となる。
よって、答えは(5)である。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
