
令和4年度下期 理論科目 問4 電験3種過去問
問題

考え方
この問題は電磁力に関する問題である。導体に働く力は、問題文で与えられている式を利用する。この問題は、他の2本の導体から受ける力をベクトル合成しないといけない。
解答例
他の2本の導体から受ける力のベクトルは図1に示すようになる。
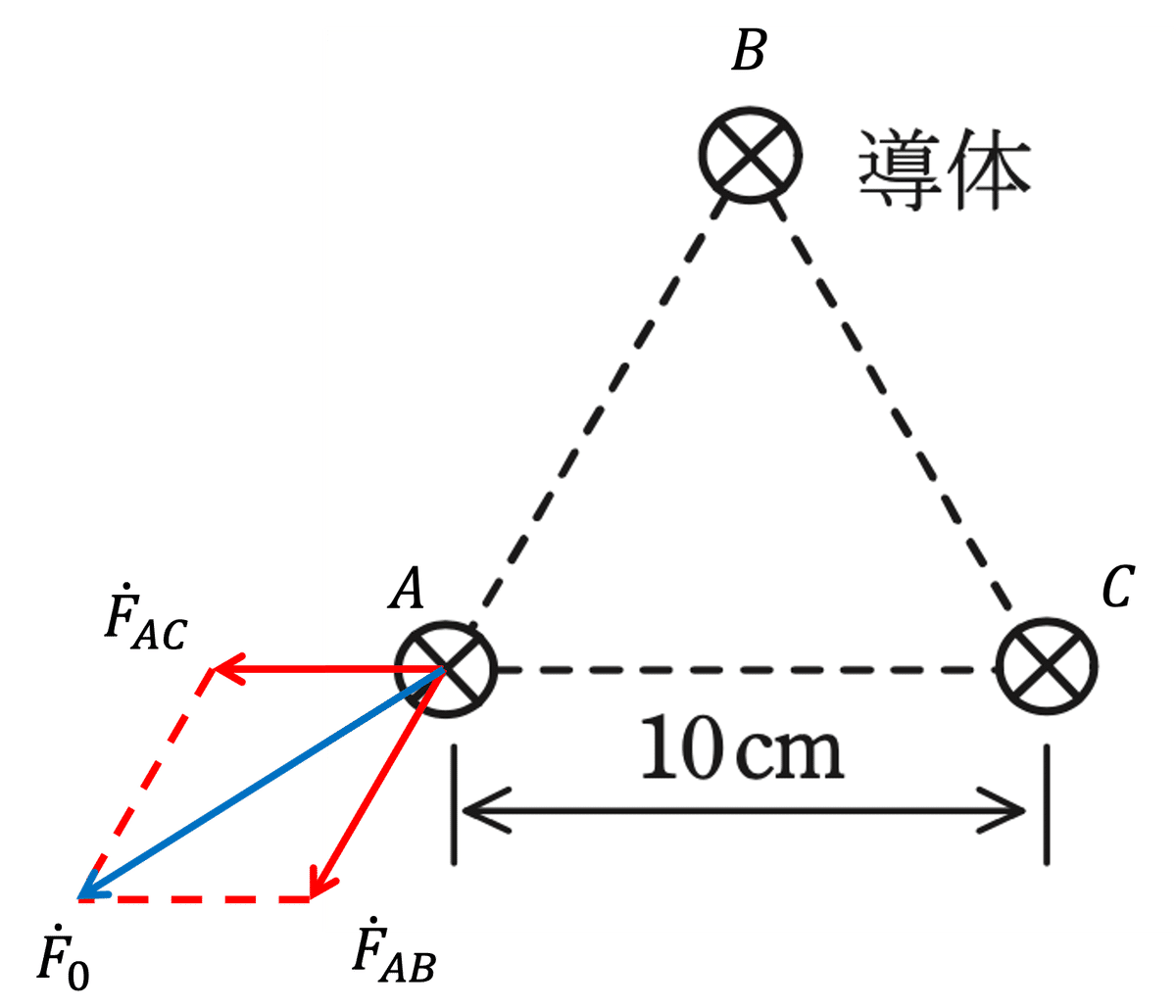
ここで、図1のベクトルが作る菱形の半分を抜き出すと図2のようになる。

図2において、緑線で示した角度は、$${60\degree}$$となる。問題文において、3本の導体は正三角形の頂点に置かれている。したがって、その対頂角となる緑線の角度は、$${60\degree}$$である。また、ベクトル$${\dot{F}_{AB}}$$と$${\dot{F}_{AC}}$$は大きさが等しいため、図2は、二等辺三角形となっており、$${\dot{F}_{0}}$$は、この二等辺三角形の底辺と垂直に交わる。これは、菱形の性質によるものである。よって、オレンジ線の角度は、二等辺三角形の性質から$${30\degree}$$となる。
結果的に図3に示す三角形が得られる。

図3の三角形は、角度の関係性から辺の比率が図3に示すようになっている。
最終的に求めたいベクトル$${\dot{F}_{0}}$$は、青線の2倍になるので、ベクトル$${\dot{F}_{0}}$$の大きさ$${F_{0}}$$は、
$$
\begin{align}
F_{0}&=2\times F_{AC}\times \frac{\sqrt{3}}{2}\notag\\
&= \sqrt{3}F_{AC}\tag{1}
\end{align}
$$
となる。ここで、ベクトル$${\dot{F}_{AC}}$$の大きさ$${F_{AC}}$$は、問題文の式より、
$$
\begin{align}
F_{AC}&=\frac{2I^{2}}{r}\times 10^{-7}\notag\\
&= \frac{2\times 7^{2}}{0.1}\times 10^{-7}\notag\\
&=9.8\times 10^{-5}\,{\rm{N/m}}\tag{2}
\end{align}
$$
と求まる。よって、ベクトル$${\dot{F}_{0}}$$の大きさ$${F_{0}}$$は、式(1)より、
$$
\begin{align}
F_{0} &= \sqrt{3}F_{AC}\notag\\
&=\sqrt{3}\times 9.8\times 10^{-5}\notag\\
&=1.697\times 10^{-4}\,{\rm{N/m}}\tag{3}
\end{align}
$$
と求まる。よって、答えは(3)である。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
